10, Joint search set
source
Geek time 2021 algorithm training camp
Author: Li Yudong
1. Merge query set
Join query set is a tree data structure, which is used to deal with the merging and query of some disjoint sets.
The idea of parallel search set is to use an array to represent the whole forest (parent). The root node of the tree uniquely identifies a set. As long as we find the tree root of an element, we can determine which set it is in.
-
Purpose: deal with the merging and query of disjointsets > > deal with grouping > > maintain unordered binary relations
-
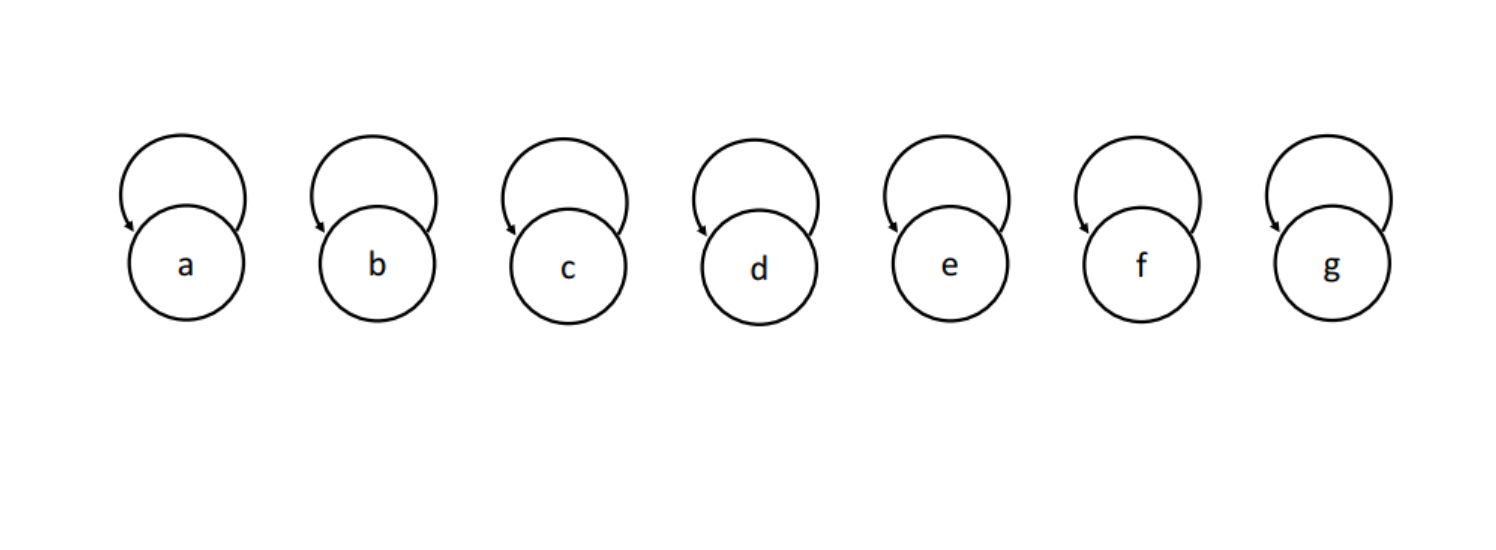
Implementation: the simplest implementation is to use only one int array fa, fa[x] represents the parent node of the node numbered x, and the fa of the root node is equal to itself
-
initialization
-
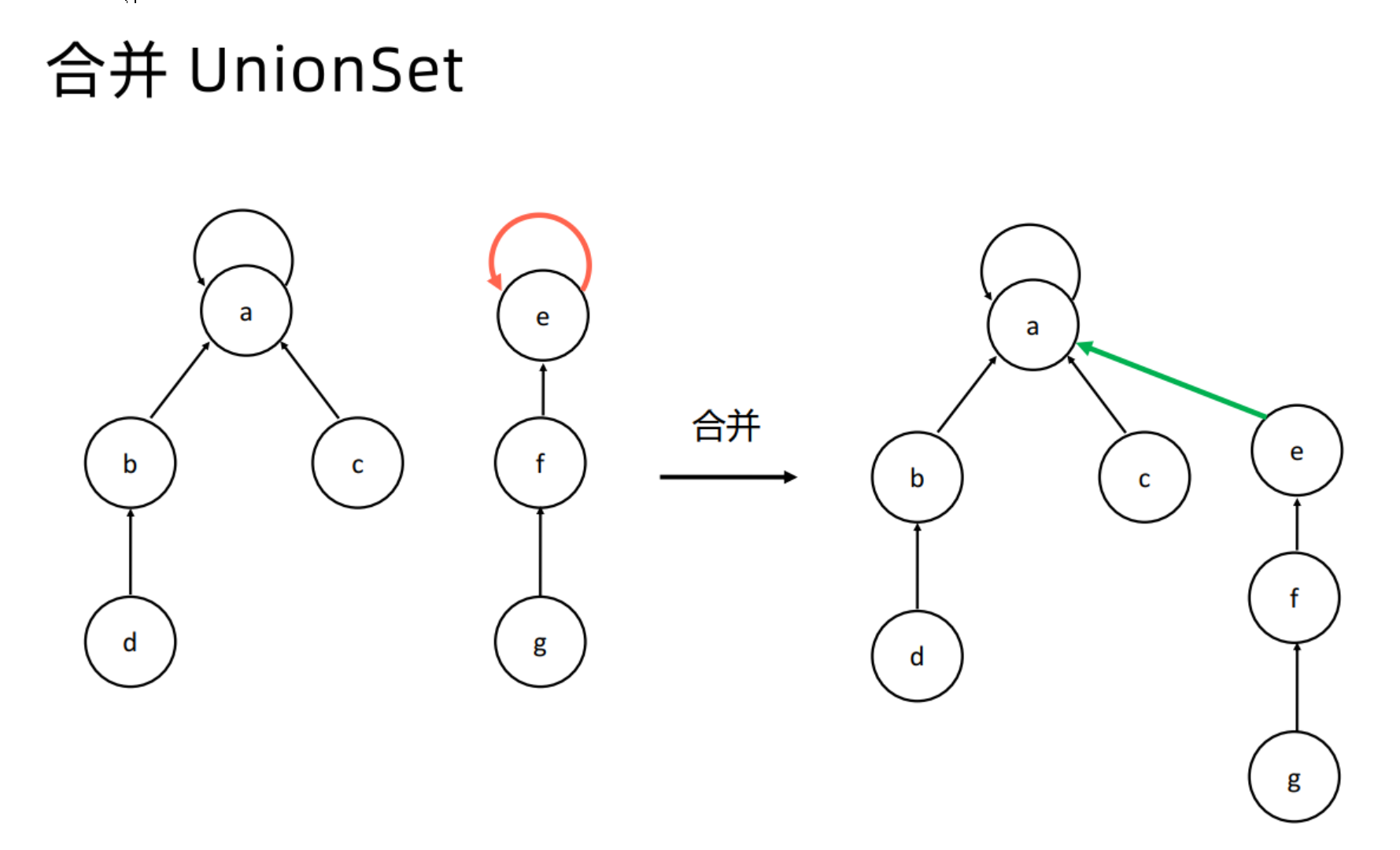
merge
-
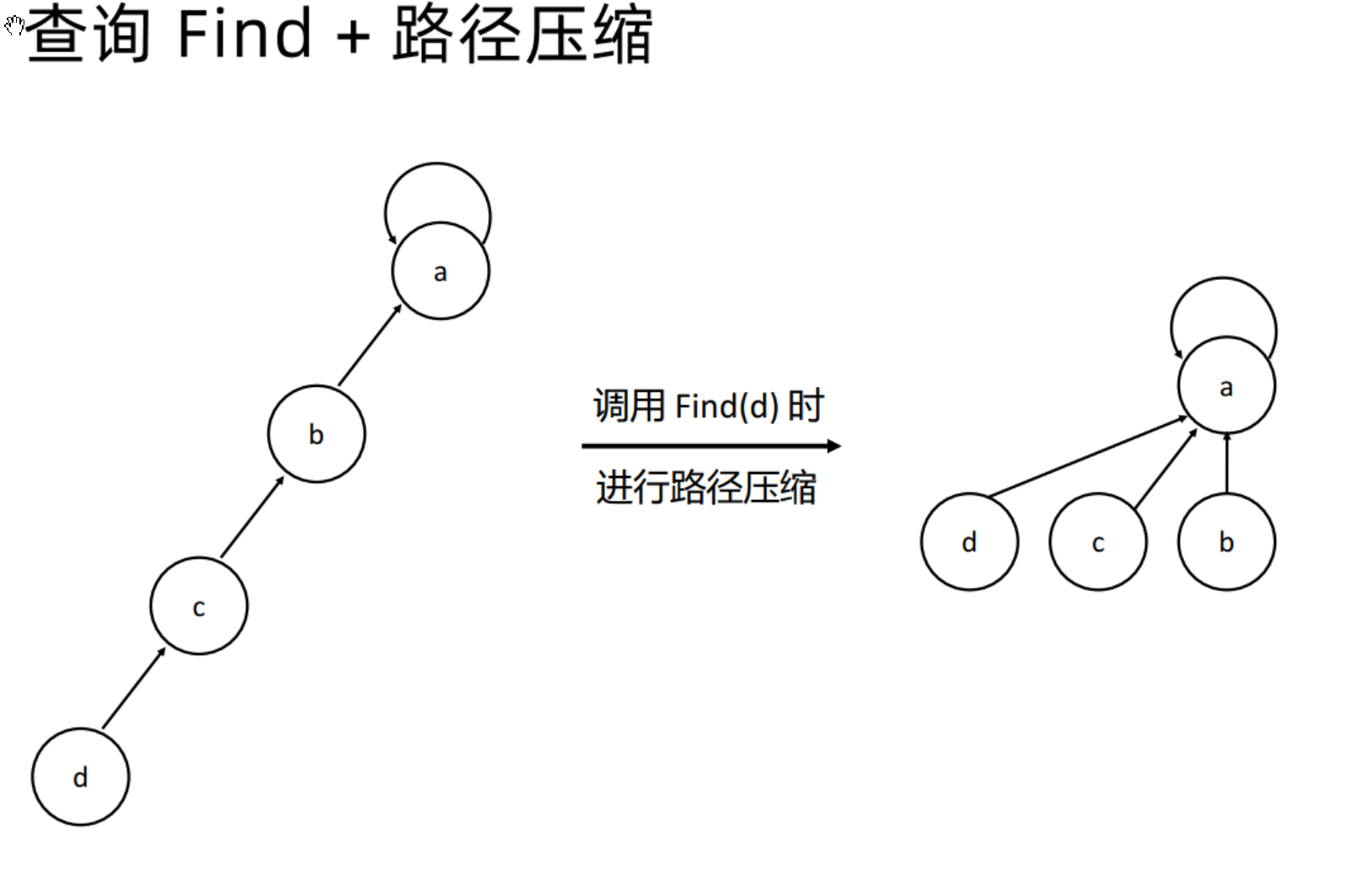
query
-
There is also an optimization called rank merging (merging deeper trees into shallower ones) or heuristic merging (merging larger trees into smaller trees)
-
At the same time, the path compression + rank merging optimized joint search set is adopted, and the average sharing complexity of a single operation is o( α (n))
-
Only one of them, O(log(n))
-
α (n) It is an inverse Ackerman function. It is a function that grows much slower than log(n). Generally, a (n) < 5
1.1 related topics
1.1.1 547 . Number of provinces
- Idea: merge the borders between adjacent cities > > > there are several provinces with several roots
class Union():
def __init__(self,n):
self.fa = [i for i in range(n)]
def find(self, x):
if self.fa[x] == x:return x
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
def unionSet(self, x, y):
x, y = self.find(x), self.find(y)
if x != y:
self.fa[x] = y
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
n, ans = len(isConnected), 0
un = Union(n)
# Merge two sets with edges
for i in range(n):
for j in range(n):
if isConnected[i][j]:
un.unionSet(i, j)
# There are several provinces with several roots
for i in range(n):
if un.find(i) == i:
ans += 1
return ans
1.1.2 130 . Surrounded area
- Idea: create an infinite area outside the area > > > connect the outside with the surrounding 'O' > > > the root is reserved for the outside
class Union():
def __init__(self,n):
self.fa = [i for i in range(n)]
self.outside = self.fa[-1]
def num(i, j):
return i
def find(self, x):
if self.fa[x] == x:return x
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
def unionSet(self, x, y):
x, y = self.find(x), self.find(y)
if x != y:
self.fa[x] = y
class Solution:
def solve(self, board: List[List[str]]) -> None:
m, n = len(board), len(board[0])
un = Union(n * m + 1)
ouside = un.fa[-1]
def num(i, j):
return i * n + j
dr = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for i in range(m):
for j in range(n):
if board[i][j] == 'X':continue
for k in dr:
ni = i + k[0]
nj = j + k[1]
if ni < 0 or nj < 0 or ni >= m or nj >= n: # If the node in the next direction is out of bounds and is O, it is connected to the outside
un.unionSet(num(i, j), un.outside)
else:
if board[ni][nj] == 'O':
un.unionSet(num(i,j), num(ni,nj))
for i in range(m):
for j in range(n):
if board[i][j] == 'O' and un.find(num(i, j)) != un.find(un.outside): #Not connected to the outside and O
board[i][j] = 'X'
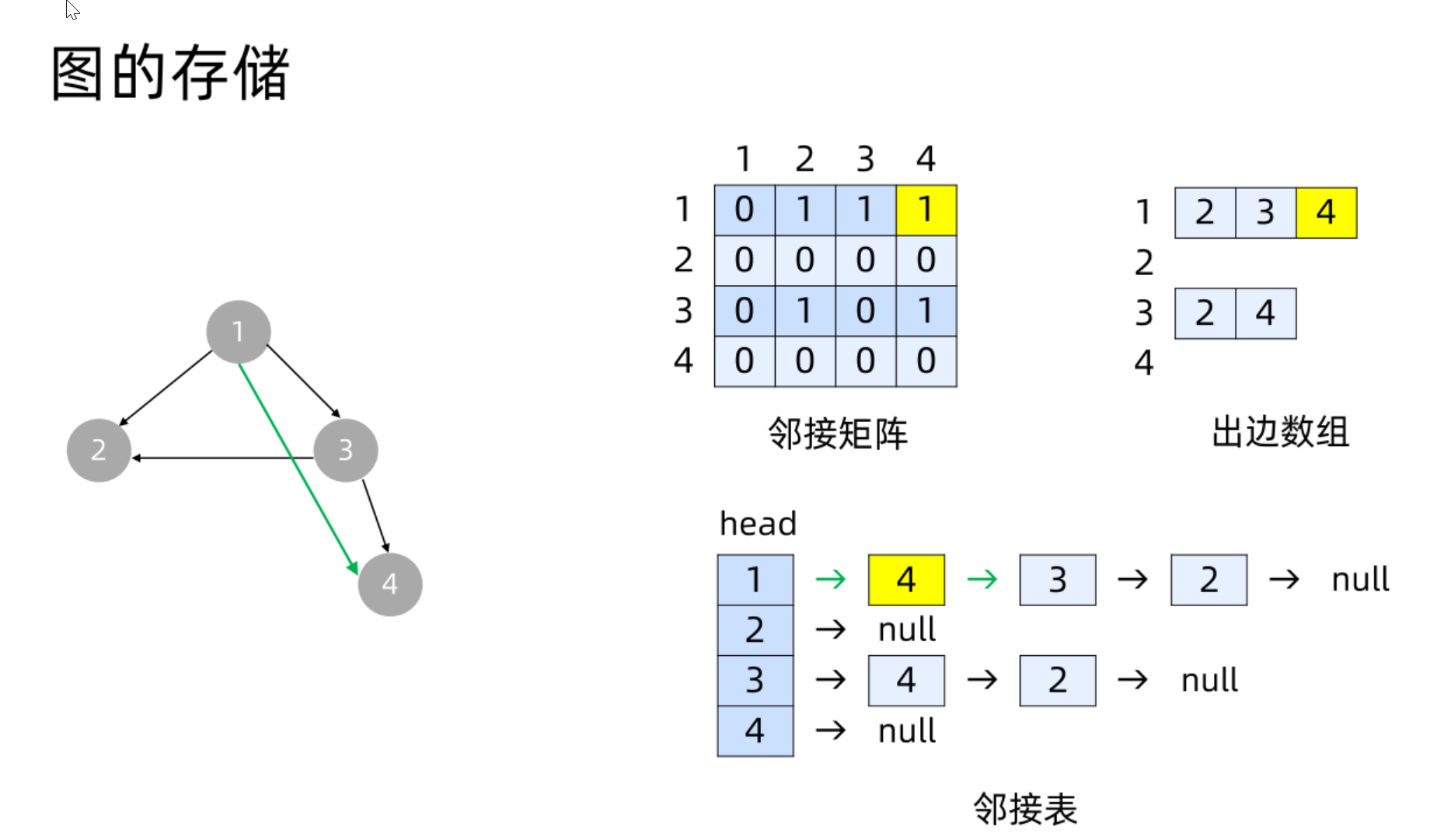
Figure 2 and related algorithms
Relationship among linked list, tree and graph: linked list is a specialized tree, and tree is a specialized graph
- Storage and addition elements of the diagram:
- Adjacency matrix: matrix O(n^2)
- Edge out array: array + array O(m + n)
- Adjacency table: array + linked list O(m + n)
2.1 Bellman Ford algorithm
-
The single source shortest path problem (SSSP problem) is:
- Given a directed graph G = (V, E), V is the point set, E is the edge set, | V|=n, |E| =m
- Nodes are numbered with consecutive integers between [1, n]
- (x,y, z) describes a directed edge from X to y with a length of Z
- Set point 1 as the starting point
Find the array dist with length n, where dist [i] represents the length of the shortest path from starting point 1 to node I
-
Bellman Ford algorithm is based on dynamic programming and iterative ideas
1 • scan all edges (x,y,z). If dist[y] > dist[x] + z, update dist[y] with dist[x] + z
2. Repeat the above steps until no update operation occurs- Time complexity O(nm)
Each round can be seen as a phase of DP
In round i, at least the shortest path with no more than i sides has been found
- Time complexity O(nm)
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
dist = [1e9] * (n + 1)
dist[k], ans = 0, 0
for i in range(1, n): #Up to n-1 cycles
updated = False
for edge in times:
x, y, z = edge
if dist[y] > dist[x] + z: #If it is smaller than the original distance, it will be updated
dist[y] = dist[x] + z
updated = True
if not updated:break
for i in range(1, n + 1):
ans = max(ans, dist[i])
return -1 if ans == 1e9 else ans
2.2 Dijkstra algorithm
- Dijkstra algorithm is based on greedy idea and is only applicable to graphs with non negative length of all edges
- Initialize dist[l] = 0, and the dist values of other nodes are positive infinity.
- Find an unlabeled node x with the smallest dist[x], and then mark node X.
- Scan all outgoing edges (x, y, z) of node X. if dist[y] > dist[x] + z, use dist[x] + z to update dist[y]
- Repeat the above 2 ~ 3 steps until all nodes are marked.
- Greedy idea: on the non negative weight graph, the global minimum dist value cannot be updated by other nodes, so you can constantly take the point with the minimum dist (each point is taken only once) and update other points
Maintaining the minimum dist value with binary heap can achieve the time complexity of O(m*log(n))
- Dijkstra – lazy delete > > > > O (n ^ 2) + M
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
dist = [1e9] * (n + 1)
dist[k], ans = 0, 0
ver = [[] for _ in range(n + 1)] #Save points and edges
edge = [[] for _ in range(n + 1)]
expand = [False] * (n + 1)
for t in times:
x, y, z = t
ver[x].append(y) #Endpoint
edge[x].append(z) #Edge weight
for r in range(1 , n + 1): #n wheel
temp = 1e9
for i in range(1, n + 1):
if not expand[i] and dist[i] < temp: #Not expanded and currently the smallest dist[i]
temp = dist[i]
min_x = i #From min_ Starting from X, consider the edge
expand[min_x] = True
for i in range(len(ver[min_x])):
y = ver[min_x][i]
z = edge[min_x][i]
if dist[y] > dist[min_x] + z:
dist[y] = dist[min_x] + z
for i in range(1, n + 1):
ans = max(ans, dist[i])
return -1 if ans == 1e9 else ans
- Dijkstra – heap > > O (m * log (n))
from heapq import *
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
dist = [1e9] * (n + 1)
dist[k], ans = 0, 0
ver = [[] for _ in range(n + 1)] #Save points and edges
edge = [[] for _ in range(n + 1)]
expand = [False] * (n + 1)
for t in times:
x, y, z = t
ver[x].append(y) #Endpoint
edge[x].append(z) #Edge weight
q = []
heappush(q, (0, k))
while q:
distance, min_x = heappop(q)
if expand[min_x]:continue #The minimum has been expanded
expand[min_x] = True
for i in range(len(ver[min_x])):
y = ver[min_x][i]
z = edge[min_x][i]
if dist[y] > dist[min_x] + z:
dist[y] = dist[min_x] + z
heappush(q, (dist[y], y))
for i in range(1, n + 1):
ans = max(ans, dist[i])
return -1 if ans == 1e9 else ans
2.3 Floyd algorithm
- Floyd algorithm can find the shortest path between each pair of points in the graph in O(n^3) time
It is essentially a dynamic programming algorithm - dp[k, i,j] indicates that the point with no more than k is the relay, and the shortest circuit from i to j
Decision: whether to use this relay point
dp[k, i,j] = min(dp[k-1, i,j], dp[k - 1, i, k] + dp[k - 1, k, j])
You can omit the first dimension and become
d[i,j] = min(d[i,j], d[i, k] + d[k,j]) - Initial state: d is the adjacency matrix (edge in the original graph)
- Comparison with Bellman Ford, Dijkstra: O(n^3) vs O(n^2*m) vs O(nmlogn)
1334 . The city with the least neighbors within the threshold distance
class Solution:
def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:
# Stored adjacency matrix d
d = [[1e9] * n for _ in range(n)]
for i in range(n):
d[i][i] = 0
for edge in edges:
x, y, z = edge
d[x][y] = d[y][x] = z
# DP -- Floyd algorithm
for k in range(n):#The relay point must be phased first
for i in range(n):
for j in range(n):
d[i][j] = min(d[i][j], d[i][k] + d[k][j]) #Relay or not
# Statistical neighbor
Minneighbour, ans = 1e9, 0
for i in range(n):
neighbour = 0
for j in range(n):
if i != j and d[i][j] <= distanceThreshold:
neighbour += 1
if Minneighbour > neighbour or (Minneighbour == neighbour and i > ans):
Minneighbour = neighbour
ans = i
return ans
2.4 Kruskal algorithm
- Kruskal algorithm always uses union search to maintain the minimum generated forest of undirected graph
1. Establish and query a set, and each point constitutes a set.
2. Sort all edges according to the weight from small to large, and scan each edge (x, y, z) in turn
3. If x and Y belong to the same set (connected), ignore this edge and continue to scan the next one.
- Otherwise, merge the sets of X and Y and add z to the answer.
- After all edge scans are completed, the edges processed in step 4 form the minimum spanning tree. The time complexity is O(mlogm)
1584 . Minimum cost of connecting all points
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
# Construct edge
edges, n, ans = [], len(points), 0
for i in range(n):
for j in range(i + 1, n): #i to j are the same as J to i
edges.append([i, j, abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])])
# Edge weight sorting
edges.sort(key = lambda x: x[2])
# Kruskal algorithm
self.fa = []
for i in range(n):
self.fa.append(i)
for edge in edges:
x, y, z = self.find(edge[0]), self.find(edge[1]), edge[2]
if x != y:
self.fa[x] = y
ans += z
return ans
def find(self, x):
if x == self.fa[x]:
return x
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
task
1 684 . Redundant connection
- Joint search set solution
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
fa = [i for i in range(n + 1)]
def find(x):
if x == fa[x]:
return x
fa[x] = find(fa[x])
return fa[x]
def unionSet(x, y):
x, y = find(x), find(y)
if x == y:
return True #Ring
else:
fa[y] = x
return False #There is no ring at present
for s, t in edges:
if unionSet(s, t):
return [s, t]
2 200 . Number of islands
- Similarly, merge search set
class Union():
def __init__(self,n):
self.fa = [i for i in range(n)]
self.outside = self.fa[-1]
def find(self, x):
if self.fa[x] == x:return x
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
def unionSet(self, x, y):
x, y = self.find(x), self.find(y)
if x != y:
self.fa[x] = y
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m, n, ans = len(grid), len(grid[0]), 0
un = Union(m * n)
def num(i, j):
return i * n + j
dr = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for i in range(m):
for j in range(n):
if grid[i][j] == '0':continue
for k in dr:
ni = i + k[0]
nj = j + k[1]
if ni < 0 or nj < 0 or ni >= m or nj >= n or grid[ni][nj] == '0':
continue
un.unionSet(num(i,j), num(ni,nj))
for i in range(m):
for j in range(n):
if grid[i][j] == '1' and un.find(num(i, j)) == num(i, j):
ans += 1
return ans