leetcode - 129. Find the sum of numbers from root node to leaf node

Give you the root node of a binary tree, root. Each node in the tree stores a number between 0 and 9. Each path from the root node to the leaf node represents a number:
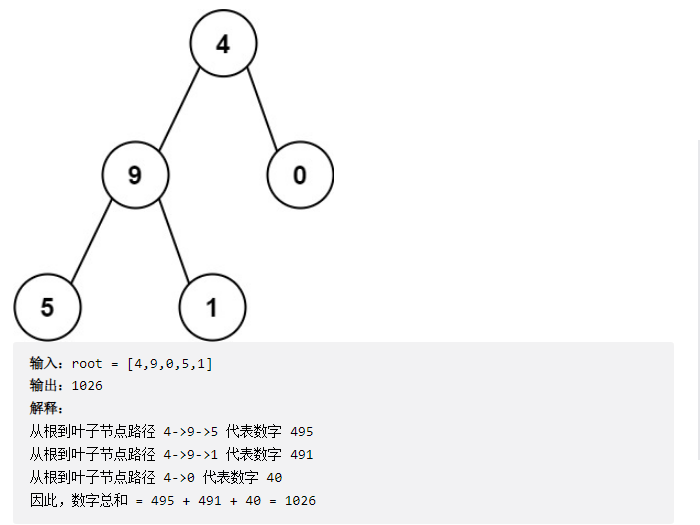
For example, the path 1 - > 2 - > 3 from the root node to the leaf node represents the number 123. Calculates the sum of all numbers generated from the root node to the leaf node.

Problem solving ideas: https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/solution/qiu-gen-dao-xie-zi-jie-dian-shu-zi-zhi-he-by-leetc/

Method 1: depth first search

class Solution {
    // Starting from the root node, traverse each node. If a leaf node is encountered, add the number corresponding to the leaf node to the sum of the numbers.
    // If the current node is not a leaf node, the corresponding number of its child nodes is calculated, and then the child nodes are traversed recursively.
    public int sumNumbers(TreeNode root) {
        if(root==null){
            return 0;
        }
        return dfs(root,0);
    }

    private int dfs(TreeNode root, int preSum) {
        // Middle order traversal: root node, left child node, right child node
        if(root==null){
            return 0;
        }
        int sum = preSum*10+root.val;
        // Leaf node encountered
        if(root.left==null && root.right==null){
            return sum;
        }
        int leftSum = dfs(root.left,sum);
        int rightSum = dfs(root.right,sum);
        return leftSum+rightSum;
    }
}

Method 2: breadth first search

class Solution {
    public int sumNumbers(TreeNode root) {
        if(root==null){
            return 0;
        }
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        Queue<Integer> numQueue = new LinkedList<>();
        nodeQueue.add(root);
        numQueue.add(root.val);
        int sum = 0;
        while (!nodeQueue.isEmpty()){
            TreeNode node = nodeQueue.poll();
            int num = numQueue.poll();
            TreeNode left = node.left;
            TreeNode right = node.right;
            if(left==null && right==null){
                sum = sum + num;
            }else{
                if(node.left!=null){
                    nodeQueue.add(left);
                    numQueue.add(num*10+left.val);
                }
                if(node.right!=null){
                    nodeQueue.add(right);
                    numQueue.add(num*10+right.val);
                }
            }
        }
        return sum;
    }
}

leetcode - 124. Maximum path sum in binary tree

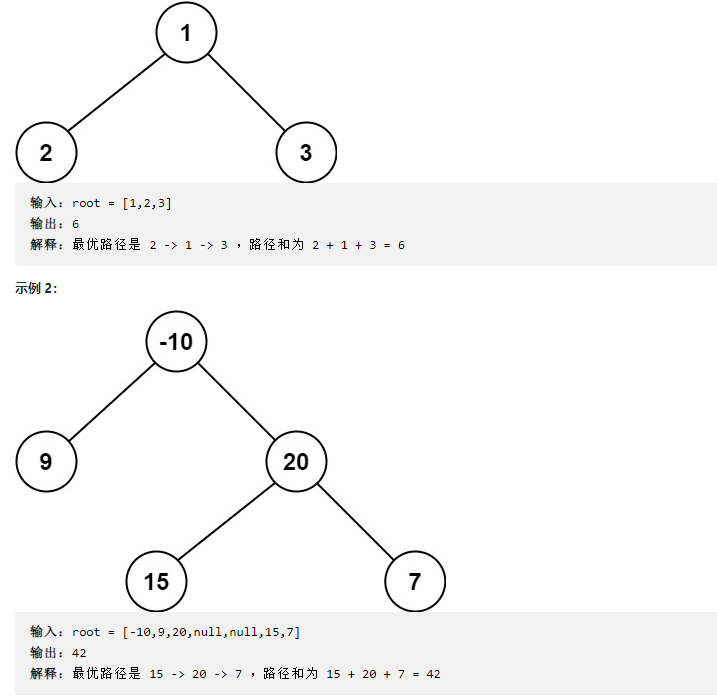
A path is defined as a sequence starting from any node in the tree and connecting along the parent node and child node to any node. The same node appears at most once in a path sequence. The path contains at least one node and does not necessarily pass through the root node.

Path sum is the sum of the values of each node in the path. Give you the root node of a binary tree, root, and return its maximum path and.

Reference ideas for problem solving; https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/solution/er-cha-shu-zhong-de-zui-da-lu-jing-he-by-leetcode-/

class Solution {
    int maxSum = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        if(root==null){
            return 0;
        }
        maxGain(root);
        return maxSum;
    }

    private int maxGain(TreeNode node) {
        if(node==null){
            return 0;
        }
        int leftGain = Math.max(maxGain(node.left),0);
        int rightGain = Math.max(maxGain(node.right),0);
        
        // Maximum path through current node and
        int pathSum = leftGain + rightGain + node.val;

        maxSum = Math.max(maxSum,pathSum);

        // Contribution value of current node
        return node.val +Math.max(leftGain,rightGain);
    }
}

leetcode - 112. Path sum I (path I with a certain value in the binary tree)

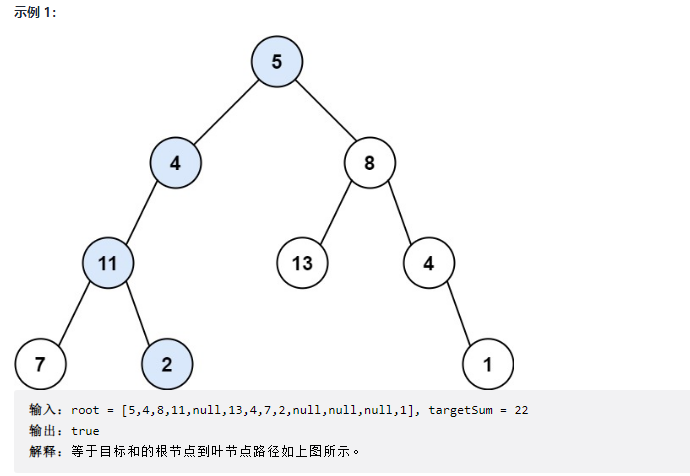
Give you the root node of the binary tree root and an integer targetSum representing the target sum. Judge whether there is a path from the root node to the leaf node in the tree. The sum of all node values on this path is equal to the target and targetSum. If it exists, return true; Otherwise, false is returned.

For problem solving ideas, please refer to: https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/

Ask if the sum of nodes on the path from the root node to a leaf node is equal to the target sum. The core idea is to traverse the tree once, and record the path and from the root node to the current node to prevent repeated calculation. It should be noted that the given root may be empty.

Method 1: breadth first search

Time complexity: O(N), where N is the number of nodes of the tree. Access once for each node.
Spatial complexity: O(N), where N is the number of nodes of the tree. The space complexity mainly depends on the overhead of the queue. The number of elements in the queue will not exceed the number of nodes in the tree.

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null){
            return false;
        }
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        Queue<Integer> sumQueue = new LinkedList<>();
        nodeQueue.add(root);
        sumQueue.add(root.val);
        while (!nodeQueue.isEmpty()){
            TreeNode node = nodeQueue.poll();
            Integer tmpSum  = sumQueue.poll();
            // Reach leaf node
            if(node.left==null && node.right==null){
                if(tmpSum==targetSum){
                    return true;
                }
            }
            if(node.left!=null){
                nodeQueue.add(node.left);
                // The path sum of the parent node plus the value of the current node is the path sum of the current node
                sumQueue.add(tmpSum+node.left.val);
            }
            if(node.right!=null){
                nodeQueue.add(node.right);
                sumQueue.add(tmpSum+node.right.val);
            }
        }
        return false;
    }
}

Method 2: depth first search

Time complexity: O(N), where N is the number of nodes of the tree. Access once for each node.
Spatial complexity: O(H), where h is the height of the tree.

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null){
            return false;
        }
        if(root.left==null && root.right==null){
            return targetSum==root.val;
        }
        return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val);
    }
}

leetcode - 113. Path sum II

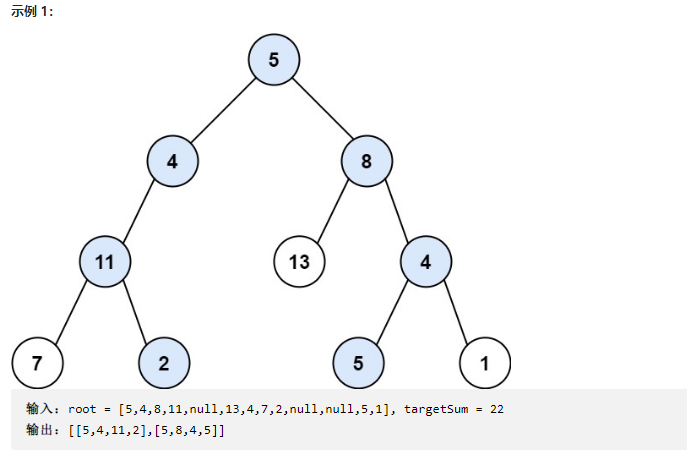
Give you the root node of the binary tree root and an integer target and targetSum, and find all the paths from the root node to the leaf node whose total path is equal to the given target sum.

For problem solving ideas, please refer to: https://leetcode-cn.com/problems/path-sum-ii/solution/lu-jing-zong-he-ii-by-leetcode-solution/
she
Note that the requirement of this problem is to find all paths where the sum of nodes on the path from the "root node" to a "leaf node" is equal to the target sum. The core idea is to traverse the tree once, and record the path and from the root node to the current node to prevent repeated calculation.

Method 1: the idea of depth first search and recursive backtracking is the same.

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
         if(root==null){
             return res;
         }
         dfs(root,new ArrayList<Integer>(),targetSum);
         return res;
    }

    private void dfs(TreeNode root, ArrayList<Integer> path, int targetSum) {
        if(root==null){
            return;
        }
        path.add(root.val);
        targetSum = targetSum-root.val;
        if(root.left==null && root.right==null){
            if(targetSum==0){
                res.add(new ArrayList<>(path));
            }
        }
        dfs(root.left,path,targetSum);
        dfs(root.right,path,targetSum);
        path.remove(path.size()-1);
    }
}

Method 2: breadth first traversal

class Solution {
    // Used to store the final results
    List<List<Integer>> res = new ArrayList<>();
    // Use a hash table to record the parent node [node,parentNode] of each node in the tree
    Map<TreeNode,TreeNode> map = new HashMap<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
         if(root==null){
             return res;
         }
         Queue<TreeNode> nodeQueue = new LinkedList<>();
         Queue<Integer> sumQueue = new LinkedList<>();
         nodeQueue.add(root);
         sumQueue.add(0);
         while (!nodeQueue.isEmpty()){
             TreeNode node = nodeQueue.poll();
             int sum = sumQueue.poll() + node.val;
             if(node.left==null && node.right==null){
                 if(sum==targetSum){
                     getPath(node);
                 }
             }
             if(node.left!=null){
                 nodeQueue.add(node.left);
                 sumQueue.add(sum);
                 map.put(node.left,node);
             }
             if(node.right!=null){
                 nodeQueue.add(node.right);
                 sumQueue.add(sum);
                 map.put(node.right,node);
             }
         }
         return res;
    }

    private void getPath(TreeNode node) {
        List<Integer> path = new ArrayList<>();
        while (node!=null){
            path.add(node.val);
            node = map.get(node);
        }
        Collections.reverse(path);
        res.add(path);
    }
}

leetcode - 104. Maximum depth of binary tree

Given a binary tree, find its maximum depth. The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node.

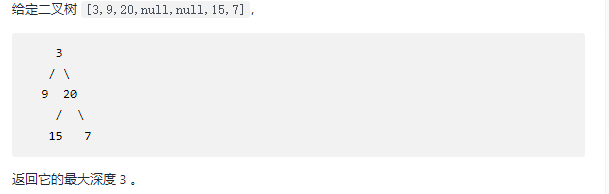
Method 1: depth first search

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth,rightDepth)+1;
    }
}

Method 2: breadth first search

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int level=0;
        while (!queue.isEmpty()){
            int size = queue.size();
            for(int i=0;i<size;i++){
                TreeNode node = queue.poll();
                if(node.left!=null){
                    queue.add(node.left);
                }
                if(node.right!=null){
                    queue.add(node.right);
                }
            }
            level++;
        }
        return level;
    }
}

leetcode - 101. Symmetric binary tree

Given a binary tree, check whether it is mirror symmetric.

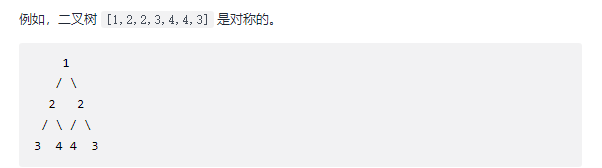
Reference ideas: https://leetcode-cn.com/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution/

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root.left,root.right);
    }

    private boolean check(TreeNode p, TreeNode q) {
        if(p==null && q==null){
            return true;
        }
        if(p==null || q==null){
            return false;
        }
        return p.val==q.val && check(p.left,q.right) && check(p.right,q.left);
    }
}

leetcode - 105. Constructing binary tree from preorder and inorder traversal sequences

Given the preorder and inorder of a tree. Construct a binary tree and return its root node.

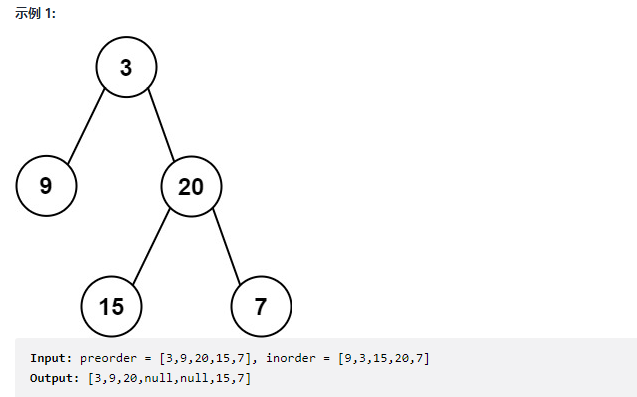
Idea:

1. The first element of the preorder traversal must be the root node
2. The root node of preorder traversal can divide the middle order traversal into left subtree, root node and right subtree
3. The first element of the left subtree in the preorder traversal can divide the result of the preorder traversal into the left subtree, the root node and the right subtree of the left subtree
4. The first element of the right subtree in the preorder traversal can divide the result of the preorder traversal into the left subtree, root node and right subtree of the right subtree

How to solve the problem:

We need to find the index corresponding to this node in the preorder traversal according to the root node of the preorder traversal, so we need to store the key and value with a HashMap first.
Then find the index of the value traversed in the middle order according to the root node traversed in the front order.

To determine:
The interval corresponding to the middle order traversal of the left subtree is [inLeft, index-1]
The interval corresponding to the middle order traversal of the right subtree is [index+1, inRight]
The corresponding interval of the left subtree traversed by the preceding sequence is [preLeft+1, (preLeft+1+index-1-inLeft) = (preleft + index inleft)]
The corresponding interval of the left subtree traversed by the preceding sequence is [preleft + index inleft + 1, preRight]

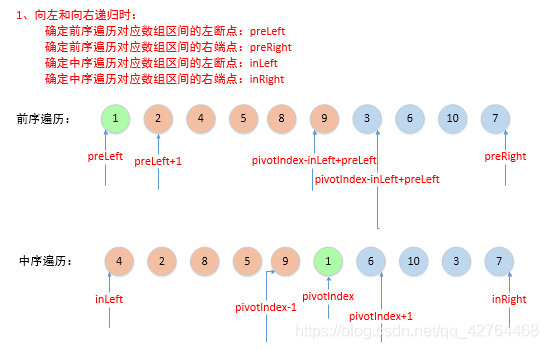
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int inleft = 0;
        int inright = inorder.length-1;
        int preleft = 0;
        int preright = preorder.length-1;

        // Find its location in inorder through the root node of preorder
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        return reBuilder(inleft,inright,preleft,preright,preorder,map);
    }

    private TreeNode reBuilder(int inleft, int inright, int preleft, int preright, int[] preorder, Map<Integer, Integer> map) {
        // Termination condition of recursion
        if(preleft>preright || inleft>inright){
            return null;
        }

        // Find root node root
        int rootValue = preorder[preleft];
        TreeNode root = new TreeNode(rootValue);

        //Find the index corresponding to the root node
        int index = map.get(rootValue);

        // Recursive reconstruction of binary tree
        root.left = reBuilder(inleft,index-1,preleft+1,preleft+index-inleft,preorder,map);
        root.right = reBuilder(index+1,inright,preleft+index-inleft+1,preright,preorder,map);
        return root;
    }
}

leetcode - 108. Convert an ordered array to a binary search tree

Give you an integer array nums, in which the elements have been arranged in ascending order. Please convert it into a highly balanced binary search tree.
A height balanced binary tree is a binary tree that satisfies the requirement that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1.

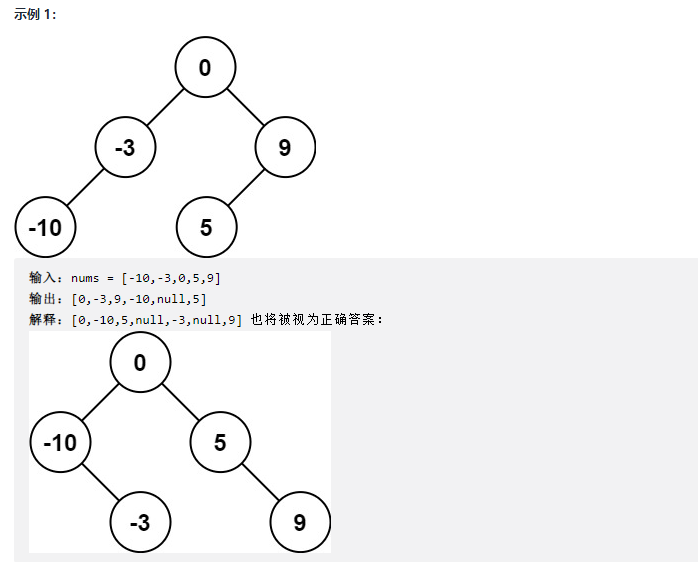
For reference: https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-33/

The middle order traversal of the binary search tree is an ascending sequence, and the array given by the topic is an ordered array sorted in ascending order, so it can be ensured that the array is the middle order traversal sequence of the binary search tree.

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        int left = 0;
        int right = nums.length-1;
        return rebuilder(nums,left,right);
    }

    private TreeNode rebuilder(int[] nums, int left, int right) {
        if(left>right){
            return null;
        }
         // Find the root node (always take the node on the left of the root node as the root node, and the node on the right can also be used)
        int mid = (left+right)/2;
        TreeNode root = new TreeNode(nums[mid]);
        
        root.left = rebuilder(nums,left,mid-1);
        root.right = rebuilder(nums,mid+1,right);
        return root;
    }
}

leetcode - Sword finger Offer 32 - III. print binary tree III from top to bottom

Please implement a function to print the binary tree in zigzag order, that is, the first line is printed from left to right, the second layer is printed from right to left, the third line is printed from left to right, and so on.

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root==null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int count = 1;

        while (!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            // The description is an odd number of layers, from left to right
            if(count % 2 ==1){
                for(int i=0;i<size;i++){
                    TreeNode node = queue.poll();
                    list.add(node.val);
                    if(node.left!=null){
                        queue.add(node.left);
                    }
                    if(node.right!=null){
                        queue.add(node.right);
                    }
                }
            }else{
                for(int i=0;i<size;i++){
                    TreeNode node = queue.poll();
                    list.add(0,node.val);
                    if(node.left!=null){
                        queue.add(node.left);
                    }
                    if(node.right!=null){
                        queue.add(node.right);
                    }
                }
            }
            count++;
            res.add(list);
        }
        return res;
    }
}

leetcode - 102. Sequence traversal of binary tree

To give you a binary tree, please return the node values obtained by traversing in sequence. (that is, access all nodes from left to right layer by layer).

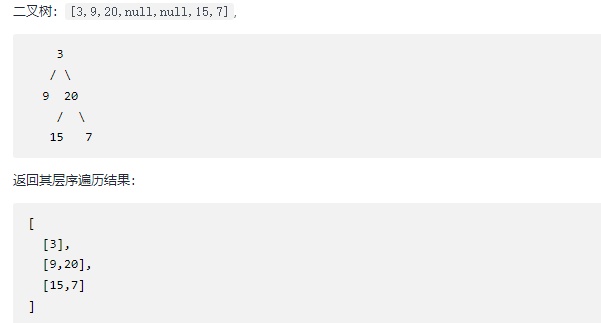
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root==null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()){
            List<Integer> list = new ArrayList<>();
            int size = queue.size();
            for(int i=0;i<size;i++){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left!=null){
                    queue.add(node.left);
                }
                if(node.right!=null){
                    queue.add(node.right);
                }
            }
            res.add(list);
        }
        return res;
    }
}

leetcode - 144. Preorder traversal of binary tree

Give you the root node of the binary tree, root, and return the preorder traversal of its node value.

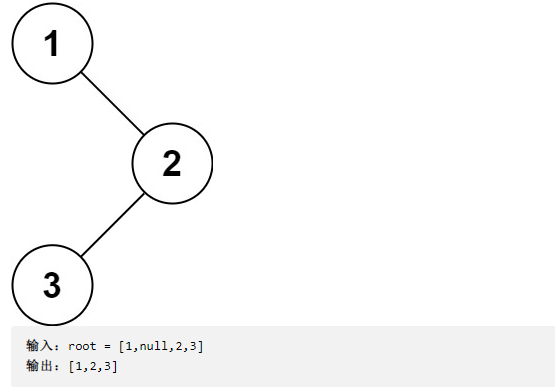
Method 1: depth first search

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root==null){
            return res;
        }
        dfs(root);
        return res;
    }

    private void dfs(TreeNode root) {
        if(root==null){
            return;
        }
        res.add(root.val);
        dfs(root.left);
        dfs(root.right);
    }
}

Method 2: breadth first search

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root==null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node!=null){
                // Preorder traversal: root node, left child node, right child node
                // Stored in the stack: right child node, left child node and root node. The currently processed node is the root node, and a null node is used to identify the root node
                if(node.right!=null){
                    stack.add(node.right);
                }
                if(node.left!=null){
                    stack.add(node.left);
                }
                stack.add(node);
                stack.add(null);
            }else{
                res.add(stack.pop().val);
            }
        }
        return res;
    }
}

leetcode - 94. Middle order traversal of binary tree

Given the root node of a binary tree, root, returns its middle order traversal.

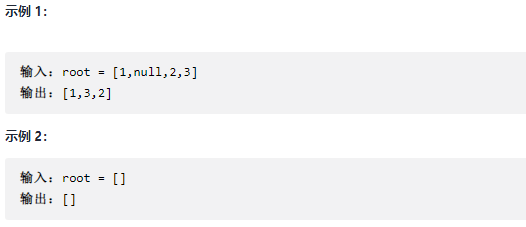
Method 1: depth first search

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root==null){
            return res;
        }
        dfs(root);
        return res;
    }

    private void dfs(TreeNode root) {
        if(root==null){
            return;
        }
        dfs(root.left);
        res.add(root.val);
        dfs(root.right);
    }
}

Method 2: breadth first search

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root==null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node!=null){
                if(node.right!=null){
                    stack.push(node.right);
                }
                stack.push(node);
                stack.push(null);
                if(node.left!=null){
                    stack.push(node.left);
                }
            }else{
                res.add(stack.pop().val);
            }
        }
        return res;
    }
}

leetcode - 145. Binary Tree Postorder Traversal

Given a binary tree, return its postorder traversal.

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if(root==null){
            return res;
        }
        dfs(root);
        return res;
    }

    private void dfs(TreeNode root) {
        if(root==null){
            return;
        }
        dfs(root.left);
        dfs(root.right);
        res.add(root.val);
    }
}

class Solution {
    List<Integer> res = new ArrayList<>();

    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) {
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                stack.push(node);
                stack.push(null);
                if (node.right != null) {
                    stack.push(node.right);
                }
                if (node.left != null) {
                    stack.push(node.left);
                }
            } else {
                res.add(stack.pop().val);
            }
        }
        return res;
    }
}