background
Data structure is the basic skill of our programmers, which is often used in daily work and job interview; Moreover, in recent years, the job competition of programmers is becoming greater and greater, and data structures and algorithms have become necessary questions in the interview of large factories. What I know: Huawei technicians must pass the machine test before they can get the interview opportunity. The machine test consists of two data structure coding questions, each with 200 points and a total score of 400240 points. Byte hopping algorithm is famous, needless to say. The meituan interviews I have experienced have also examined data structures and algorithms.
Because our daily development work often focuses on the preparation of business logic code and runs on excellent frameworks such as Spring, although the data structure of JDK is skillfully used, we have little understanding of the underlying logic and data structure, so this leads to the problem of data structure and algorithm in the interview becoming "sending proposition". Therefore, our developers need to pay more attention to these commonly used data structures and algorithms in their daily work, spend their efforts in peacetime and accumulate more, so that they can be handy in job hunting.
problem
Recently, some colleagues interviewed several large factories and asked about the data structure related to the linked list, such as whether the single linked list has rings and ring entry detection, single linked list element de duplication, single linked list inversion, etc. I studied and practiced "whether there is a ring in the single linked list and the problem of ring entry detection", which I share with you as a daily accumulation. Through the following figure, we can understand the two situations of single linked list with and without rings.
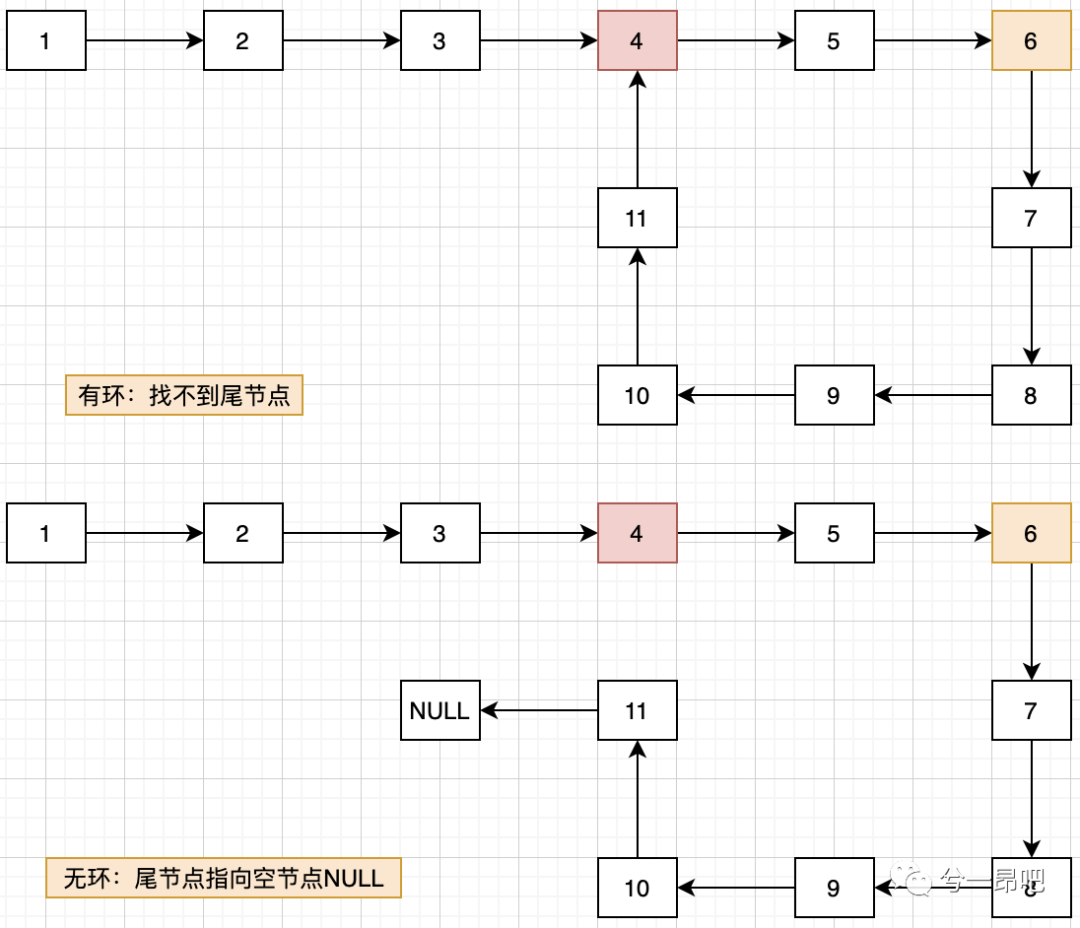
image.png
As the first article of the linked list, let's look at how to build the linked list. For the sake of simplicity, the code is as follows. For the convenience of the next demonstration, I provide two construction methods of linked list. The first method aims to create a single linked list from front to back according to the input array; the second method aims to create a linked list with a ring according to the fact that there is only one repeating element in the input array sequence.
/**
* struct Node
*/
public class Node {
public Node(int data) {
this.data = data;
next = null;
}
public int data;
public Node next;
}
/**
* Build linked list (acyclic)
*/
private static Node buildLinklist(int[] texts) {
Node head = new Node(0);
Node node = head;
for (int text : texts) {
Node next = new Node(text);
node.next = next;
node = next;
}
return head;
}
/**
* To build a linked list, there may be links
*/
private static Node buildCircleLinklist(int[] texts) {
Node head = new Node(0);
Node node = head;
// Stores nodes that have been created
Map<Integer, Node> nodeMap = new HashMap<>();
for (int text : texts) {
Node next = null;
if (nodeMap.containsKey(text)) {
next = nodeMap.get(text);
} else {
next = new Node(text);
nodeMap.put(text, next);
}
node.next = next;
node = next;
}
return head;
}Solution 1: auxiliary space method
Whether the single linked list has a ring and the entry detection of the ring can be known from the title. These are actually two problems. First, check whether there are rings in the single linked list; Second, if there is a ring, find the entry node of the ring. Therefore, we must solve the first problem first.
When traversing the linked list from the head node, we will find that if there are links in the linked list, we will not be able to find the tail node of the linked list. Once the traversal process enters the ring, the traversal process will rotate in the ring and never stop; If there are no rings in the linked list, our traversal process will stop in limited steps. Therefore, from the perspective of linked list traversal, we can find the difference between linked and acyclic lists:
• acyclic: in limited steps, we can find the tail node of the linked list, that is, there is a node pointing to an empty address. • Ring: the tail node can never be found and will loop within the ring.
Just imagine: if our traversal process has memory and remembers all the nodes passed by (each node is unique in terms of memory), we will draw the following conclusions:
• acyclic: each node is different from beginning to end in the traversal process. The result in the figure above is: 1-2-3-4-5-6-7-8-9-10-11; • With ring: in the traversal process, once entering the loop process, the nodes in the ring will appear repeatedly. The results in the figure above are: 1-2-3-4-5-6-7-8-9-10-11-4-5-6-7-8-9-10-11-4-5-6.
Therefore, I have come to the first solution today, that is, with the help of auxiliary space, store the unique information of all passing nodes in the traversal process, and check whether each node has been repeated. If no duplicate node is found at the end of the traversal process, it can be said that the chain table is acyclic; If there is node duplication during traversal, it indicates that the linked list has a ring, and the first repeated element is the entry of the ring.
A supplementary note: the unique information of the Node is identified by the hashCode of the Node object. For the Node class, I did not override the hashCode() method, which represents the memory address of the object.
The specific implementation code is as follows:
/**
* Check whether there are links in the linked list: use the unique information of node and cooperate with HashMap
*
* @param head Head node
* @return If it is empty, there is no ring; If it is not empty, the output is the entry node
*/
private static Node detectCircleByExtraSpace(Node head) {
// Use this map to store all traversed nodes
Map<Integer, Node> nodeHashCodeMap = new HashMap<>();
Node node = head.next;
// If the node is not empty, continue to traverse. There are two conditions for the loop to stop: one is to traverse to the end of the linked list node, and the other is to find duplicate elements.
while (node != null) {
// Get node hashCode
Integer hashCode = node.hashCode();
// Determine whether it has been traversed
if (nodeHashCodeMap.containsKey(hashCode)) {
// If it has been traversed, there is a ring, and this is the entrance
return node;
}
// Add map after traversal
nodeHashCodeMap.put(node.hashCode(), node);
// next
node = node.next;
}
// Come here, it means there is no ring.
return null;
}Next, you can write a piece of code to test. The following example uses the sequence "1, 2, 3, 4, 5, 6, 3" to create two kinds of linked lists with and without rings, as shown in the following figure; Then use detectCircleByExtraSpace to detect. For acyclic, it should output "acyclic", for looped, it should output "looped, and the inlet is: 3".
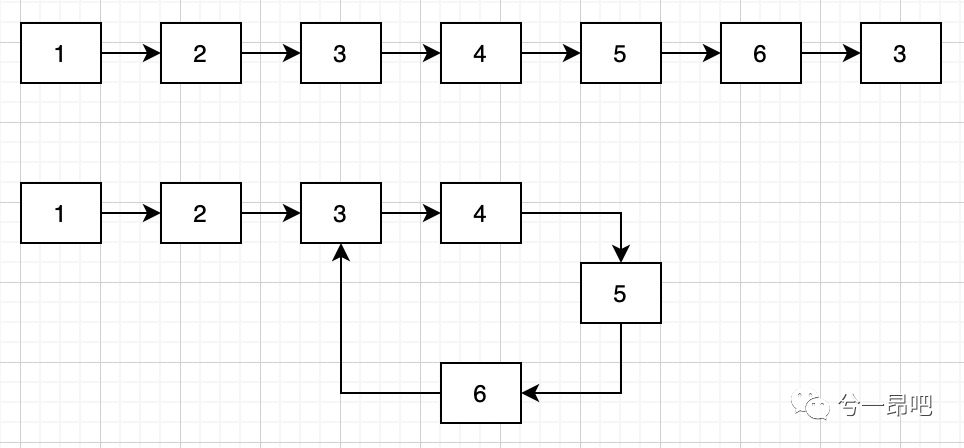
image.png
public static void main(String[] args) {
int[] texts = {1, 2, 3, 4, 5, 6, 3};
Node head = buildCircleLinklist(texts);
Node node = detectCircleByExtraSpace(head);
printResult(node);
head = buildLinklist(texts);
node = detectCircleByExtraSpace(head);
printResult(node);
}
private static void printResult(Node node) {
if (node == null) {
System.out.println("exannulate");
} else {
System.out.println("With ring, the inlet is:" + node.data);
}
}In the above example, the output results are as follows, which meet the expectations.
Ring, inlet: 3 exannulate
Solution 2: fast and slow pointer method
Friends who are familiar with this problem should think of using the speed pointer to solve this problem when they see the problem. At the beginning, I can only understand whether there is a ring in the inspection. I always don't understand the entrance inspection. After a while of company derivation, I can figure it out. The key to this solution lies in how to understand the problem and the derivation of some mathematical formulas after understanding the problem. I'll try to explain the solution principle of the fast and slow pointer.
First look at the detection of linked list links. If the linked list with a ring is compared to a one-way track and can only run in the direction of the arrow, the runner will eventually turn around in the circular track. Suppose that Party A and Party B are running in the same direction along the runway, in which Party A's speed is twice that of Party B; Then, a will enter the circular runway first and keep circling, and B will enter the circular runway again. After both Party A and Party B enter the circular runway, it becomes a "catch-up problem" in the travel problem. Since Party A's speed is greater than that of Party B, Party A will certainly catch up with Party B after a period of time. Of course, if there is no ring in the linked list and a's speed is greater than B, then a will run to the end first and will not meet B in the process.
Therefore, we can use the above "tracking problem" method to solve the detection problem of linked list links. Set two pointers fast and slow to traverse backward from the head of the linked list. The speed of fast is twice that of slow. If fast can "catch up" with slow, it indicates that there are links in the linked list; If the fast traversal is completed and reaches the tail node, it indicates that there is no ring in the linked list.
Then analyze how to find the entrance of the ring. Let's first say the conclusion: if there are rings in the linked list, after the fast and slow pointers meet, move the fast pointer to the head of the linked list; Then fast and slow move at the same speed (one node at a time). When they meet, the meeting point is the entrance of the ring. How to deduce it is explained in combination with the following figure:
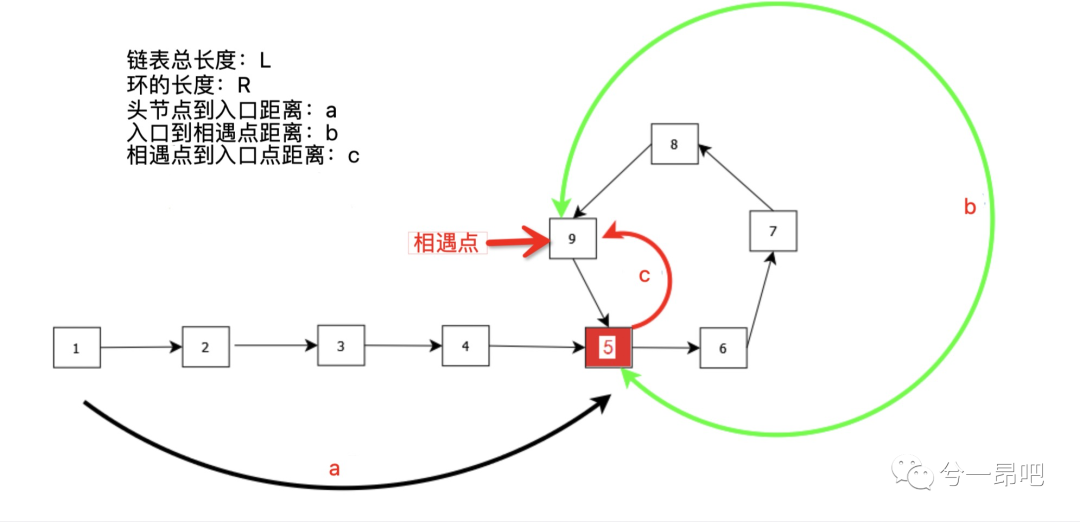
Let's make a few assumptions:
• assume that the distance from the head node to the ring entrance is a, the distance from the ring entrance to the fast and slow encounter points is B, and the distance from the encounter point to the ring entrance is c; • Suppose that the length of the linked list is L and the length of the ring is R; • Assuming that slow travels a distance of S, fast travels a distance of 2S (fast may go around n times in addition to a+b).
Then, there will be the derivation of the following formula:
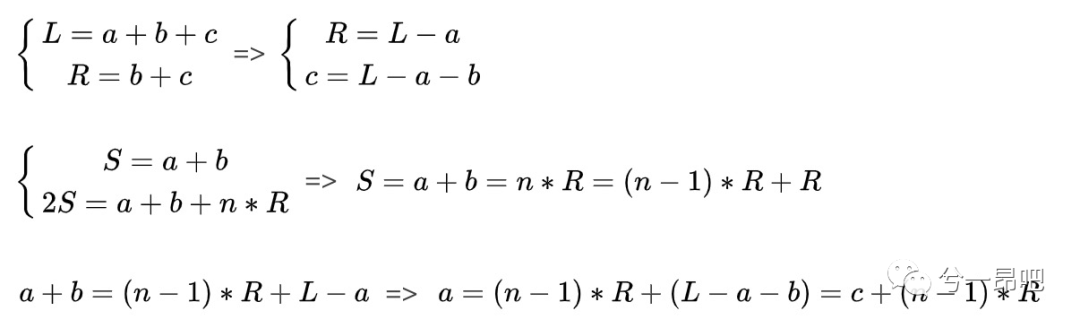
In combination with the above conclusion (that is, after fast and slow meet, fast moves from the first node, slow continues to move from the meeting point, and fast's speed is consistent with slow), take a closer look at what this formula represents?
• a represents the distance from the head node to the ring entrance, which is equivalent to the distance traveled by fast; • c+(n-1)*R represents n-1 circles along the ring after walking from the slow point to the ring entrance; • If the above two are equal, it means that fast and slow will meet at the entrance of the ring;
So: if there are rings in the linked list, after the fast and slow pointers meet, move the fast pointer to the head of the linked list; Then fast and slow move at the same speed (one node at a time). When they meet, the point where they meet is the entrance of the ring.
The above is the principle and process of fast and slow pointer solution, which is actually easier to understand. However, if I haven't met or heard of it, it's really hard for me to think of this solution, especially the second step to find the ring entrance. Well, after the theoretical analysis, let's see how to implement the code:
/**
* Check whether the linked list has rings. If there are rings, find the entry
* Using fast and slow pointers
*
* @param head Chain header node
* @return If it is empty, there is no ring; If it is not empty, the output is the entry node
*/
private static Node detectCircleByFastSlow(Node head) {
// The speed pointer starts from the beginning node
Node fast = head;
Node slow = head;
// Used to record meeting points
Node encounter = null;
// fast takes two steps at a time, so ensure next and next Next is not empty. If it is empty, it means there is no ring
while (fast.next != null && fast.next.next != null) {
// fast takes two steps and slow takes one step
fast = fast.next.next;
slow = slow.next;
// Fast and slow are the same, indicating that they met, or fast caught up with slow.
if (fast == slow) {
// Record the meeting point. fast or slow are the same
encounter = fast;
// When they meet, they exit the ring detection process
break;
}
}
// If the encounter is empty, it means there is no ring, so you don't have to continue looking for the ring entrance.
if (encounter == null) {
return encounter;
}
// fast returns to the head position
fast = head;
// As long as the two don't meet, go on
while (fast != slow) {
// fast takes one step at a time, slow takes one step at a time, and the speed is the same
fast = fast.next;
slow = slow.next;
}
// The meeting point is the ring entrance
return fast;
}Modify the above test code and you will find that it is consistent with the result of solution 1.
public static void main(String[] args) {
int[] texts = {1, 2, 3, 4, 5, 6, 3};
Node head = buildCircleLinklist(texts);
Node node = detectCircleByFastSlow(head);
printResult(node);
head = buildLinklist(texts);
node = detectCircleByFastSlow(head);
printResult(node);
}summary
In this paper, "auxiliary space method" and "fast and slow pointer method" are used to solve the classical problem of judging whether a single linked list has a ring and finding the ring entry. The two methods have their own advantages and disadvantages, which are briefly summarized as follows:
• auxiliary space method: the time complexity is O(n) and the space complexity is O(n). The advantage is easy to think of and understand; The disadvantage is that it will consume additional auxiliary space; • Fast and slow pointer method: the time complexity is O(n) and the space complexity is O(1). Good performance, but not easy to understand.
The importance of data structure and algorithm has been mentioned at the beginning of the article. I would like to add some more: although it seems difficult, these common problems and solutions are fixed. As long as we accumulate more, practice more, think more, and apply them flexibly to our work, we will find that it is not as difficult as we imagined.