As we all know, java 1.7 and the previous HashMap linked list insert elements using the header insertion method, which will lead to rings in the linked list in a multi-threaded environment, and will fall into an dead loop when being searched (CPU burst) 😭). Java 1.8 optimizes this problem and uses head interpolation. What's the difference between tail interpolation and head interpolation?
Preliminary knowledge: capacity expansion mechanism of HashMap
Put the source code here first:
void resize(int newCapacity) {
...
Entry[] newTable = new Entry[newCapacity];
// New and old table conversion
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
// 1. Traverse the old table
for (Entry<K,V> e : table) {
// 2. If the element is not empty, traverse the Entry element
while(null != e) {
//Save the next node of e first
next = e.next;
...
//Recalculate subscript (due to length change)
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
// 3. Put elements into a new table
newTable[i] = e;
// 4. Continue to traverse the Entry child nodes
e = next;
}
}
}
It can be seen that there are two steps in capacity expansion:
- Create a new Entry array with twice the capacity
- Copy the old Entry array to the new array
As the length of the Entry array becomes longer, the subscript of the original node may change. This is because the subscript is calculated by: (n - 1) & hash. For the same hash value, if the length changes, the resulting subscript may be different.
By the way, the initial capacity of HashMap is 16. As long as n is the power of 2, the binary of n - 1 must be all 1. Assuming there are i bits, it must keep the last i bits of hash when it does & operation with any hash (& both operations are 1 is 1), which is very uniform and not easy to conflict.
Back here, copy the elements of the old array to the new array. If it is tail interpolation, you have to traverse the whole linked list. The complexity is O (N), while the complexity of head interpolation is only O (1). So why use tail interpolation?
Let's first look at the head insertion method. Borrow a big man's picture: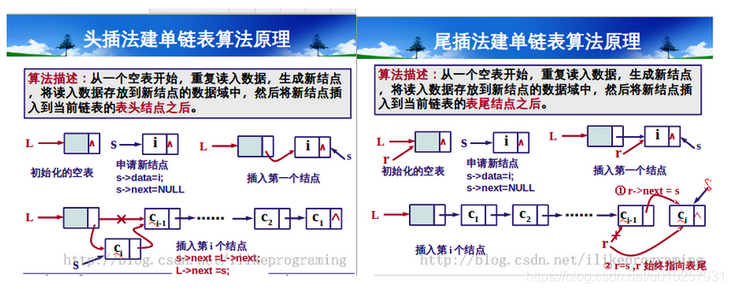
It can be seen that when inserting a new node, the header insertion method is to first point the next of the new node to c1 (L.next), and then set L.next as the new node. If in a multithreaded environment, the linked list corresponding to the key value k is k = a - > b - > null,
1. Thread a runs first and put s element c. at this time, expand the capacity and copy the element step by step. After copying a, the new linked list is a - > null
2. At this time, thread B runs, put elements d and B are also expanded, and the linked list in B becomes B - > A - > null
3. At this time, a runs again and copies b. the new linked list in a is b - > A - > null. At this time, a's capacity expansion is completed
4. Then B runs. At this time, the original array has been expanded by a, and the linked list corresponding to k becomes B - > A - > null. At this time, the traversed element should be the byte point a of element B, so at this time, a will insert a new array to form a - > b - > a ring, and the program falls into an endless loop.
In addition, in the multi-threaded environment, the node of put will be lost. Not here.
In contrast, if the tail insertion method is inserted from the tail, there will be no ring problem, because it is inserted to the tail every time.
final Node<K,V>[] resize() {
...
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
// The node has no hash conflict and is directly migrated to the new table
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// Red black tree structure
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// There is hash conflict and it is not a red black tree structure
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// Tail interpolation replication
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
However, there will still be the problem of node loss. Therefore, it can be seen that hashmap is thread unsafe. Because of this disadvantage, CocurrentHashMap is mostly used in multi-threaded environment.
reference resources: