Hello, everyone. Today I will show you a very advanced tool, SMT solver. It has a wide range of applications, such as solving various equations, solving various programming problems (such as Sudoku), solving logic problems, etc.

Today Xiao Ming will show you the highlights:

🎨 Z3 solver 🎨

🔦 brief introduction 🔫

Z3 solver is an SMT solver developed by Microsoft Research. It is used to check the satisfiability of logical expressions and can find one of the feasible solutions in a set of constraints. The disadvantage is that it can not find all the feasible solutions (for programming problems, it can be scipy).

Z3 solver can be applied to software / hardware verification and testing, constraint solving, hybrid system analysis, safety, biology, geometric solving and so on. Z3 is mainly developed by C + +, and provides language call interfaces such as. NET, C, C + +, Java and python. The python interface is explained below.

z3 can be installed directly through pip:

pip install z3-solver

Reference example: https://ericpony.github.io/z3py-tutorial/guide-examples.htm

There are three types of variables in z3, namely integer (Int), real (Real) and vector (BitVec).

For integer type data, the basic API:

1. Int(name, ctx=None), create an integer variable, and name is the name
2. Ints (names, ctx=None) to create multiple integer variables. Names are space separated names
3. IntVal (val, ctx=None) creates an integer constant with an initial value and no name.

The API of real number type is consistent with that of integer type, while the vector (BitVec) is slightly different:

1. Bitvec(name,bv,ctx=None) creates a bit vector. Name is his name and bv represents size
2. BitVecs(name,bv,ctx=None) creates a bit vector with multiple variables. Name is the name and bv is the size
3. BitVecVal(val,bv,ctx=None) creates a bit vector with an initial value and no name.

Simplify (expression) to simplify the expression that can be simplified.

For complete API documentation, refer to: https://z3prover.github.io/api/html/namespacez3py.html

Let's take a look at the basic usage of z3:

🔀 Mathematical operation 🎦

Start with a simple example:

♊ ⅸ binary linear equation ♋ ️

For example, use z3 to solve the binary linear equation:

x − y = 3 x-y = 3 x−y=3

3 x − 8 y = 4 3x-8y=4 3x−8y=4

solve directly:

from z3 import *

x, y = Reals('x y')
solve(x-y == 3, 3*x-8*y == 4)

[y = 1, x = 4]

If you need to get the result of the specified variable, you can use the Solver:

1. s=solver(), create a solution object.
2. s. Add (condition) to add a limiting condition to the solution
3. s.check(), check whether the solution exists. If so, it will return "sat"
4. Module(), output the solution result

x, y = Reals('x y')
solver = Solver()
qs = [x-y == 3, 3*x-8*y == 4]
for q in qs:
    solver.add(q)
if solver.check() == sat:
    result = solver.model()
print(result)
print("x =", result[x], ", y =", result[y])

[y = 1, x = 4]
x = 4 , y = 1

You can view the constraints that the solver has added and the number of constraints through solver.assertions():

assertions = solver.assertions()
print(assertions)
print(len(assertions))

[x - y == 3, 3*x - 8*y == 4]
2

If you need to remove constraints, you need to call the solver.push() method before adding constraints.

Let's take the following equation as an example:

x > 10 x > 10 x>10

y = x + 2 y = x + 2 y=x+2

Get results:

x, y = Ints('x y')
solver = Solver()
solver.add(x > 10, y == x + 2)
print("Current constraint:", solver.assertions())
if solver.check() == sat:
    print("result:", solver.model())
else:
    print(solver.check())

Current constraint: [x > 10, y == x + 2]
result: [x = 11, y = 13]

Next, we add another constraint y < 11 that can be deleted:

solver.push()
solver.add(y < 11)
print("Current constraint:", solver.assertions())
if solver.check() == sat:
    print("result:", solver.model())
else:
    print(solver.check())

Current constraint: [x > 10, y == x + 2, y < 11]
unsat

It can be seen that there is no effective solution under this constraint.

Delete the constraint and calculate again:

solver.pop()
print("Current constraint:", solver.assertions())
if solver.check() == sat:
    print("result:", solver.model())
else:
    print(solver.check())

Current constraint: [x > 10, y == x + 2]
result: [x = 11, y = 13]

⚠️ Note: if you do not push constraints, directly pop will result in Z3Exception: b'index out of bounds' error.

🚦 Linear polynomial constraint 🚧

The constraints are:
x > 2 y < 10 x + 2 ∗ y = 7 x > 2 \\ y < 10 \\ x + 2 * y = 7 \\ x>2y<10x+2∗y=7
The above constraints x and y are integers. We need to find one of the feasible solutions:

x, y = Ints('x y')
solve([x > 2, y < 10, x + 2*y == 7])

result:

[y = 0, x = 7]

Of course, there is more than one practical solution, z3 only one of which can be found.

💧 Nonlinear polynomial constraint 🌌

The constraints are:

x 2 + y 2 > 3 x^2 + y^2 > 3 x2+y2>3

x 3 + y < 5 x^3 + y < 5 x3+y<5

The above constraints x and y are real numbers. We need to find one of the feasible solutions:

x, y = Reals('x y')
solve(x**2 + y**2 > 3, x**3 + y < 5)

result:

[y = 2, x = 1/8]

A feasible solution was soon calculated.

I have demonstrated some basic examples above. Let's continue to share some comprehensive cases:

💫 Problems related to uniform speed linear motion in senior high school physics 📰

The uniform speed linear motion formula in high school physics is:

s = v i t + 1 2 a t 2 s=v_it + \frac12at^2 s=vi​t+21​at2

v f = v i + a t v_f=v_i + at vf​=vi​+at

For example, press the brake when moving forward at the speed of 30m/s, if the acceleration of deceleration is − 8 m / s 2 -8m/s^2 − 8m/s2, what is the braking distance of the vehicle after braking?

Direct problem solving:

s, v_i, a, t, v_f = Reals('s v__i a t v__f')

equations = [
    s == v_i*t + (a*t**2)/2,
    v_f == v_i + a*t,
]
print("Equation of motion:", equations)

variables = [
    v_i == 30,
    v_f == 0,
    a == -8
]
print("Parameter variable:", variables)
print("result:")
solve(equations + variables)

Equation of motion: [s == v__i*t + (a*t**2)/2, v__f == v__i + a*t]
Parameter variable: [v__i == 30, v__f == 0, a == -8]
result:
[a = -8, v__f = 0, v__i = 30, t = 15/4, s = 225/4]

It can be seen that the braking distance is 225/4m and the braking duration is 15/4s.

To get the result of the specified variable, you need the Solver:

solver = Solver()
equations = [
    s == v_i*t + (a*t**2)/2,
    v_f == v_i + a*t,
]
variables = [
    v_i == 30,
    v_f == 0,
    a == -8
]
solver.add(equations + variables)
if solver.check() == sat:
    result = solver.model()
print(f"Braking distance:{result[s].as_decimal(4)}m，Braking time:{result[t].as_decimal(4)}s")

Braking distance: 56.25m，Braking time: 3.75s

Here, we have already started to use z3. Let me continue to demonstrate some more advanced content and use z3 to solve some programming problems:

📜 Comprehensive programming problems 📈

📐 Solution Sudoku ✏️

I demonstrated before that the program automatically plays Sudoku:

• <Let the program automatically play Sudoku games and turn you into an ashes Sudoku player in seconds>
• <Python calls C language to realize Sudoku computing logic and speed up 100 times>

In this paper, for a difficult Sudoku, the time-consuming of python optimized algorithm is up to 3.2 seconds, and the time-consuming of core logic rewritten in C language is up to milliseconds.

Next, I use z3 solver to solve this problem, so that pure Python can achieve good performance without using other languages.

First, we create constraints according to the rules of Sudoku game:

from z3 import *

# 9x9 integer variable matrix
X = [[Int(f"x_{i}_{j}") for j in range(9)]
     for i in range(9)]

# Each cell contains a value in 1,2,3,... 8,9
cells_c = [And(1 <= X[i][j], X[i][j] <= 9)
           for i in range(9) for j in range(9)]

# Each number can appear at most once per line
rows_c = [Distinct(X[i]) for i in range(9)]

# Each number in each column can appear at most once
cols_c = [Distinct([X[i][j] for i in range(9)])
          for j in range(9)]

# Each 3x3 square and each number can appear at most once
sq_c = [Distinct([X[3*i0 + i][3*j0 + j]
                  for i in range(3) for j in range(3)])
        for i0 in range(3) for j0 in range(3)]
# Sudoku integrity constraints
sudoku_c = cells_c + rows_c + cols_c + sq_c

Still for the Sudoku that took more than 3 seconds in Python:

# For Sudoku to be solved, 0 means empty cell
board = [
    [0, 0, 0, 6, 0, 0, 0, 3, 0],
    [5, 0, 0, 0, 0, 0, 6, 0, 0],
    [0, 9, 0, 0, 0, 5, 0, 0, 0],
    [0, 0, 4, 0, 1, 0, 0, 0, 6],
    [0, 0, 0, 4, 0, 3, 0, 0, 0],
    [8, 0, 0, 0, 9, 0, 5, 0, 0],
    [0, 0, 0, 7, 0, 0, 0, 4, 0],
    [0, 0, 5, 0, 0, 0, 0, 0, 8],
    [0, 3, 0, 0, 0, 8, 0, 0, 0]
]

Solution:

def solveSudoku(board: list):
    board_c = [If(board[i][j] == 0,
                  True,
                  X[i][j] == board[i][j])
               for i in range(9) for j in range(9)]

    s = Solver()
    s.add(sudoku_c + board_c)
    if s.check() == sat:
        m = s.model()
        r = [[m[X[i][j]].as_long() for j in range(9)]
             for i in range(9)]
        return r
solveSudoku(board)

It can be seen that the results have been calculated in more than 0.3 seconds, and the results are consistent with the previous results:

🍞 Eight queens problem 🍩

There is an 8x8 chessboard. I hope to put 8 pieces (Queen) in it. There can be no other piece in the row, column and diagonal of each piece.

In the following figure, the left figure is a method that meets the conditions, and the left figure does not meet the conditions. The eight queens' problem is to find a way to meet this requirement:

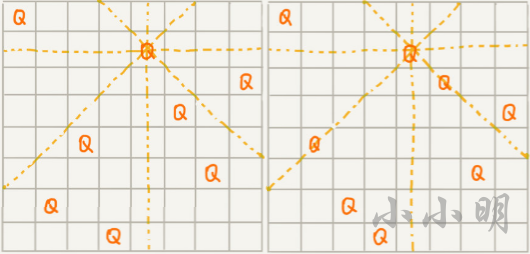
If we need to find all the solutions that meet the conditions, we only want to use the backtracking algorithm for recursive solution, but if we only need one feasible solution, we can use the z3 solver.

Create constraints first:

# Each queen must record the corresponding column position of the queen in different rows
Q = [Int(f'Q_{i}') for i in range(8)]

# Each queen is in columns 0,1,2,..., 7
val_c = [And(0 <= Q[i], Q[i] <= 7) for i in range(8)]

# Up to one queen per column
col_c = [Distinct(Q)]

# Diagonal constraint
diag_c = [If(i == j,
             True,
             And(Q[i] - Q[j] != i - j, Q[i] - Q[j] != j - i))
          for i in range(8) for j in range(i)]

A feasible solution can be obtained by direct solution, in which the column position of each queen:

solve(val_c + col_c + diag_c)

result:

[Q_3 = 5,
 Q_1 = 1,
 Q_7 = 6,
 Q_5 = 2,
 Q_4 = 0,
 Q_0 = 3,
 Q_2 = 7,
 Q_6 = 4]

Of course, we can print the results more clearly:

def print_eight_queen(result):
    for column in result:
        for i in range(8):
            if i == column:
                print(end="Q  ")
            else:
                print(end="*  ")
        print()


s = Solver()
s.add(val_c + col_c + diag_c)
if s.check() == sat:
    result = s.model()
    result = [result[Q[i]].as_long() for i in range(8)]
    print("Column position of each row:", result)
    print_eight_queen(result)

result:

Column position of each row: [5, 3, 1, 7, 4, 6, 0, 2]
*  *  *  *  *  Q  *  *  
*  *  *  Q  *  *  *  *  
*  Q  *  *  *  *  *  *  
*  *  *  *  *  *  *  Q  
*  *  *  *  Q  *  *  *  
*  *  *  *  *  *  Q  *  
Q  *  *  *  *  *  *  *  
*  *  Q  *  *  *  *  *  

🎡 Installation dependency problem 🌈

There are often dependencies and conflicts when installing programs. You can easily solve the correct installation order of packages through z3.

For example:

1. Package a depends on packages b, c, and z
2. Package b depends on package d
3. Package c, depending on d or e, and f or g
4. Package d conflicts with package e
5. Package d conflicts with package g

Suppose that the package a code to be installed is as follows:

from z3 import *

a, b, c, d, e, f, g, z = Bools('a b c d e f g z')
# 1. Package a depends on packages b, c and z
q1 = And([Implies(a, dep) for dep in [b, c, z]])
# 2. Package b depends on package d
q2 = Implies(b, d)
# 3. Package c, depending on d or e, and f or g
q3 = Implies(c, And([Or(d, e), Or(f, g)]))
# 4. Package d conflicts with package e
q4 = Or(Not(d), Not(e))
# 5. Package d conflicts with package g
q5 = Or(Not(d), Not(g))

s = Solver()
# Installation package a
s.add(a, q1, q2, q3, q4, q5)
if s.check() == sat:
    m = s.model()
    # x() returns the Z3 expression, and x.name() returns the string
    r = [x.name() for x in m if is_true(m[x])]
    print("install a:")
    print(r)
else:
    print("Invalid installation configuration")

install a:
['z', 'b', 'd', 'f', 'c', 'a']

To facilitate calling, we can encapsulate dependencies and conflicts into separate methods:

def DependsOn(pack, deps):
    if is_expr(deps):
        return Implies(pack, deps)
    else:
        return And([Implies(pack, dep) for dep in deps])


def Conflict(*packs):
    return Or([Not(pack) for pack in packs])


def install_check(*problem):
    s = Solver()
    s.add(problem)
    if s.check() == sat:
        m = s.model()
        # x() returns the Z3 expression, and x.name() returns the string
        r = [x.name() for x in m if is_true(m[x])]
        print(r)
    else:
        print("Invalid installation configuration")

Call install a again:

a, b, c, d, e, f, g, z = Bools('a b c d e f g z')

print("install a:")
install_check(
    a,
    DependsOn(a, [b, c, z]),
    DependsOn(b, d),
    DependsOn(c, [Or(d, e), Or(f, g)]),
    Conflict(d, e),
    Conflict(d, g),
)

install a:
['z', 'b', 'd', 'f', 'c', 'a']

Installation a and g:

print("install a and g:")
install_check(
    a,
    g,
    DependsOn(a, [b, c, z]),
    DependsOn(b, d),
    DependsOn(c, [Or(d, e), Or(f, g)]),
    Conflict(d, e),
    Conflict(d, g),
)

install a and g:
Invalid installation configuration

You can see that z3 successfully calculates the conflicting a and g.

🎢 Logic problem 🚊

After solving the programming problem, we finally play two logic problems:

🚫 Who is the thief 🗿

A military warehouse was stolen. The public security department has the following clues: ① at least one of the three persons a, B and C is a thief; ② If a is a thief, B must be an accomplice; ③ When the theft happened, B was watching a movie in the cinema. From this you can deduce ().

A. A, B and C are thieves
B. Both a and B are thieves
C. C is a thief
D. A is a thief

Complete problem solving Code:

# abc stands for whether a, B and C are thieves respectively
a, b, c = Bools('a b c')
# At least one of the three was a thief
q1 = Or(a, b, c)
# If a is a thief, B must be an accomplice;
q2 = Implies(a, b)
# B must not be
q3 = Not(b)

s = Solver()
s.add(q1, q2, q3)

options = [
    # A, B and C are thieves
    And(a, b, c),
    # Both a and B are thieves
    And(a, b),
    # C is a thief
    c,
    # A is a thief
    a
]
result = []
for answer, option in zip("ABCD", options):
    s.push()
    s.add(option)
    print(answer, s.check(), s.assertions())
    if s.check() == sat:
        result.append(answer)
    s.pop()
print("Final answer:", "".join(result))

A unsat [Or(a, b, c), Implies(a, b), Not(b), And(a, b, c)]
B unsat [Or(a, b, c), Implies(a, b), Not(b), And(a, b)]
C sat [Or(a, b, c), Implies(a, b), Not(b), c]
D unsat [Or(a, b, c), Implies(a, b), Not(b), a]
Final answer: C

It can be seen from the above results that only the result of Article 3 is sat (with solution), indicating that the corresponding option C is correct.

⛔ Coal mine accident ✴️

The topics are as follows:

A major accident occurred in a large coal mine. The people at the scene of the accident concluded as follows:

Miner A: the accident was caused by equipment problems;
Miner B: someone violated the operating procedures, but the cause of the accident was not equipment problems;
Miner C: if the cause of the accident is equipment problems, someone violates the operating procedures;
Miner D: the cause of the accident was equipment problems, but no one violated the operating procedures.

If only one of the above four people's conclusions is true, the following may be true is ().

A. Miner A's conclusion is true
B. Miner B's conclusion is true
C. Miner Ding's conclusion is true
D. Miner C's conclusion is true and someone has violated the operating procedures
E. Miner C's conclusion is true, and no one violates the operating procedures

First, we need to define two propositions in the topic, whether there is a problem with the equipment and whether someone violates the operating procedures.

Complete problem solving Code:

equipment = Bool('equipment')  # Is there a problem with the equipment
violation = Bool('violation')  # Violation of operating procedures
qs = [
    # A: the accident was caused by equipment problems;
    equipment,
    # B: someone has violated the operating procedures, but the cause of the accident is not equipment problems;
    And(violation, Not(equipment)),
    # C: if the cause of the accident is equipment problem, someone violates the operating procedures;
    Implies(equipment, violation),
    # D: the accident was caused by equipment problems, but no one violated the operation
    And(equipment, Not(violation)),
]

s = Solver()
# Only one of the above four people's conclusions is true
s.add(Sum([If(q, 1, 0) for q in qs]) == 1)
# Judge whether each option is correct one by one
options = [qs[0], qs[1], qs[3], And(
    qs[2], violation), And(qs[2], Not(violation))]
result = []
for answer, option in zip("ABCDE", options):
    s.push()
    s.add(option)
    print(answer, s.check(), s.assertions())
    if s.check() == sat:
        result.append(answer)
    s.pop()
print("Final answer:", "".join(result))

result:

A unsat [If(equipment, 1, 0) +
 If(And(violation, Not(equipment)), 1, 0) +
 If(Implies(equipment, violation), 1, 0) +
 If(And(equipment, Not(violation)), 1, 0) ==
 1,
 equipment]
B unsat [If(equipment, 1, 0) +
 If(And(violation, Not(equipment)), 1, 0) +
 If(Implies(equipment, violation), 1, 0) +
 If(And(equipment, Not(violation)), 1, 0) ==
 1,
 And(violation, Not(equipment))]
C unsat [If(equipment, 1, 0) +
 If(And(violation, Not(equipment)), 1, 0) +
 If(Implies(equipment, violation), 1, 0) +
 If(And(equipment, Not(violation)), 1, 0) ==
 1,
 And(equipment, Not(violation))]
D unsat [If(equipment, 1, 0) +
 If(And(violation, Not(equipment)), 1, 0) +
 If(Implies(equipment, violation), 1, 0) +
 If(And(equipment, Not(violation)), 1, 0) ==
 1,
 And(Implies(equipment, violation), violation)]
E sat [If(equipment, 1, 0) +
 If(And(violation, Not(equipment)), 1, 0) +
 If(Implies(equipment, violation), 1, 0) +
 If(And(equipment, Not(violation)), 1, 0) ==
 1,
 And(Implies(equipment, violation), Not(violation))]
Final answer: E

These are the common applications of z3 solver. Have you paid the tuition? I also want to learn how to solve programming problems in python. Remember to pay attention to me and wait for the next issue~

I'm Xiao Ming. I'll see you next time~