content

Describe the relationship between violent recursion and dynamic programming

Memory search cache

Dynamic programming can be improved by violent recursion to solve the routine of dynamic programming

Common attempt models

Principles of design trial process

This section is the general outline of violence recursion to dynamic programming (very important)

The subsequent lessons are all about this series of routines

1,attempt=> Identify all parameters, find all variable parameters and fixed values (boundaries)
2,What is the combination of variable parameters? The table size is determined according to the variation range of variable parameters
3,Given the dependence of fixed position, there are examples of specific parameters (both ends of the range)
4,Know the final desired position in the table, baseCase Fixed row and column (OK) baseCase)
5,Analyze dependencies anywhere

Topic 1: robot location

Suppose there are n positions in a row, which are recorded as 1~N, and N must be greater than or equal to 2
At the beginning, the robot is in position m (M must be one of 1~N)
If the robot comes to position 1, the next step can only go to position 2 to the right;
If the robot comes to position N, the next step can only go to position N-1 to the left;
If the robot comes to the middle position, the next step can go left or right;
How many methods stipulate that the robot must take K steps and finally reach position P (P is also one of 1~N)
Given four parameters N, M, K and P, return the number of methods

1) cache method:

Use HashMap to store the current state

public static void main(String[] args) {
    System.out.println(ways1(5, 2, 4, 6));
}

public static int ways1(int N, int start, int aim, int K) {
    if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
        return -1;
    }
    HashMap<String, Integer> cache = new HashMap<>();

    return process(start, K, aim, N, cache);
}

// The robot still has a rest step to go,
// The ultimate goal is aim,
// What are the locations? 1~N
public static int process(int cur, int res, int aim, int N, HashMap<String, Integer> cache) {
    String key = String.valueOf(cur) + "_" + String.valueOf(res);
    if (cache.containsKey(key)) {
        return cache.get(key);
    }
    // baseCase
    int ans = 0;
    if (res == 0) {
        ans = cur == aim ? 1 : 0;
        cache.put(key, ans);
        return ans;
    }
    // Boundary condition
    if (cur == 1) {
        ans = process(cur + 1, res - 1, aim, N, cache);
        cache.put(key, ans);
        return ans;
    }
    if (cur == N) {
        ans = process(cur - 1, res - 1, aim, N, cache);
        cache.put(key, ans);
        return ans;
    }
    // Any case
    ans = process(cur - 1, res - 1, aim, N, cache)
            + process(cur + 1, res - 1, aim, N, cache);
    cache.put(key, ans);
    return ans;
}

2) cache into array

By changing the cache to an array of the specified size, the space complexity is reduced

// The robot still has a rest step to go,
// The ultimate goal is aim,
// What are the locations? 1~N
public static int process(int cur, int res, int aim, int N, int[][] cache) {
    if (cache[cur][res] != 0 ) {
        return cache[cur][res];
    }
    // baseCase
    int ans = 0;
    if (res == 0) {
        ans = cur == aim ? 1 : 0;
        cache[cur][res] = ans;
        return ans;
    }
    // Boundary condition
    if (cur == 1) {
        ans = process(cur + 1, res - 1, aim, N, cache);
        cache[cur][res] = ans;
        return ans;
    }
    if (cur == N) {
        ans = process(cur - 1, res - 1, aim, N, cache);
        cache[cur][res] = ans;
        return ans;
    }
    // Any case
    ans = process(cur - 1, res - 1, aim, N, cache)
            + process(cur + 1, res - 1, aim, N, cache);
    cache[cur][res] = ans;
    return ans;
}

3) Continue to simplify

public class Test {
    public static void main(String[] args) {
        System.out.println(ways1(5, 2, 4, 6));
    }

    public static int ways1(int N, int start, int aim, int K) {
        if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
            return -1;
        }
        int[][] dp = new int[N + 2][K + 1];
        for (int i = 0; i <= N; i++) {
            for (int j = 0; j <= K; j++) {
                dp[i][j] = -1;
            }
        }
        return process(start, K, aim, N, dp);
    }

    // The robot still has a rest step to go,
    // The ultimate goal is aim,
    // What are the locations? 1~N
    public static int process(int cur, int rest, int aim, int N, int[][] dp) {
        if (dp[cur][rest] != -1) {
            return dp[cur][rest];
        }

        int ans = 0;
        if (rest == 0) {
            ans = cur == aim ? 1 : 0;
        } else if (cur == 1) {
            ans = process(2, rest - 1, aim, N, dp);
        } else if (cur == N) {
            ans = process(N - 1, rest - 1, aim, N, dp);
        } else {
            ans = process(cur - 1, rest - 1, aim, N, dp)
                    + process(cur + 1, rest - 1, aim, N, dp);
        }
        dp[cur][rest] = ans;
        return ans;
    }
}

4) dp process

Draw the table:
Dynamic programming is to directly overhead the idea of violence recursion and take out the corresponding determined value for calculation

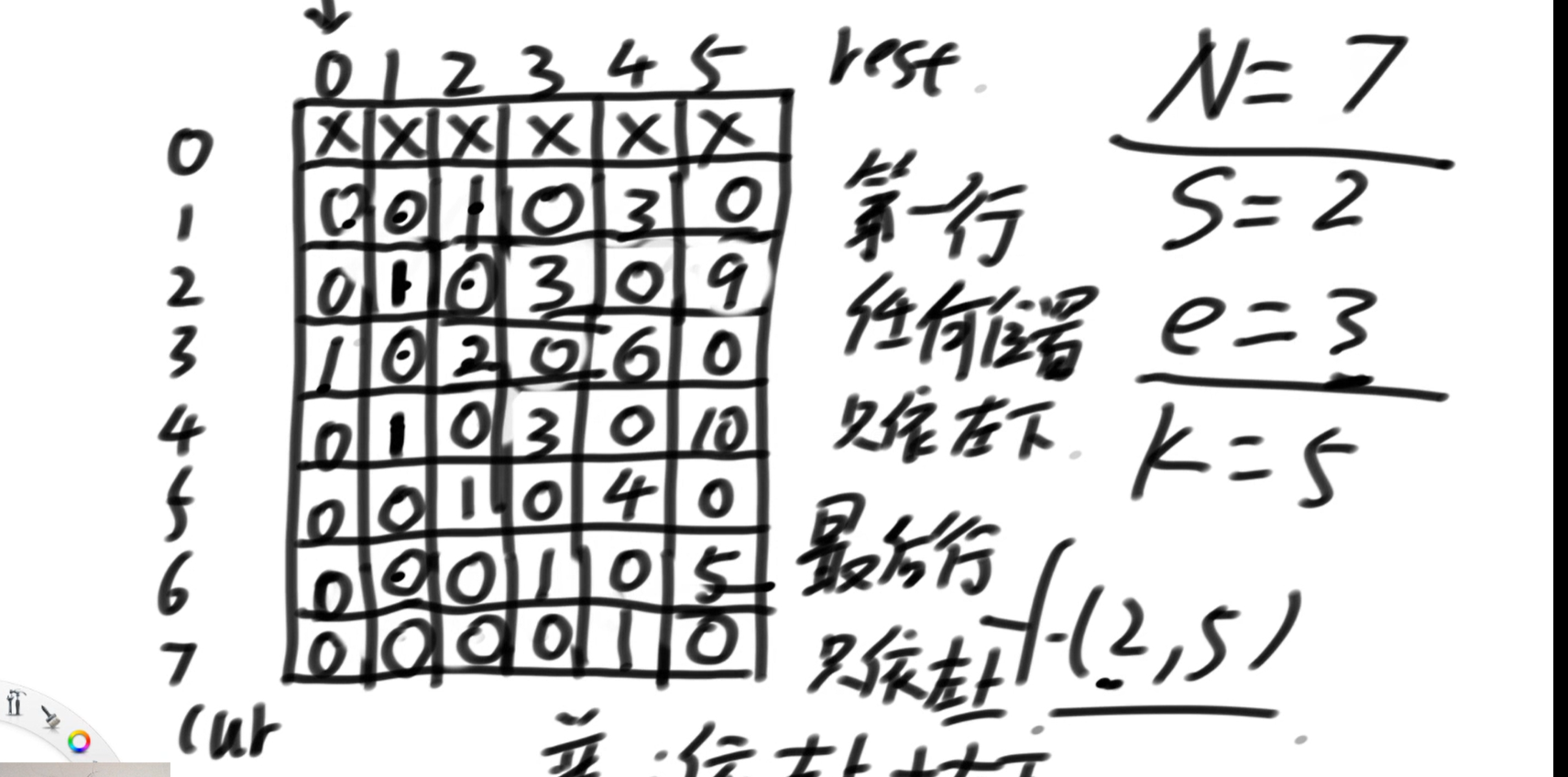
public class Test {
    public static void main(String[] args) {
//        K: Remaining steps
        System.out.println(process(2, 4, 6, 5));
    }

    // The robot still has a rest step to go,
    // The ultimate goal is aim,
    // What are the locations? 1~N
    public static int process(int start, int aim, int K, int N) {
        if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
            return -1;
        }
        int[][] dp = new int[N + 1][K + 1];

        // cur has reached aim, and the remaining steps are 0
        dp[aim][0] = 1;
//        Dealing with other situations
        for (int rest = 1; rest <= K; rest++) {
            dp[1][rest] = dp[2][rest - 1];
            for (int cur = 2; cur < N; cur++) {
                dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];
            }
            dp[N][rest] = dp[N - 1][rest - 1];
        }

        return dp[start][K];
    }
}

Topic 2: draw game

Given an integer array arr, cards with different values are arranged in a line
Player A and player B take each card in turn
It is stipulated that player A takes it first and player B takes it later
But each player can only take the leftmost or rightmost cards at a time
Player A and player B are extremely smart
Please return the score of the final winner

Solution:

	// According to the rules, the score of the winner is returned
	public static int win1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int first = f1(arr, 0, arr.length - 1);
		int second = g1(arr, 0, arr.length - 1);
		return Math.max(first, second);
	}

	// arr[L..R], the best score obtained first returns
	public static int f1(int[] arr, int L, int R) {
		if (L == R) {
			return arr[L];
		}
		int p1 = arr[L] + g1(arr, L + 1, R);
		int p2 = arr[R] + g1(arr, L, R - 1);
		return Math.max(p1, p2);
	}

	// //arr[L..R], the best score obtained by the backhand is returned
	public static int g1(int[] arr, int L, int R) {
		if (L == R) {
			return 0;
		}
		int p1 = f1(arr, L + 1, R); // The opponent took the number of L positions
		int p2 = f1(arr, L, R - 1); // The number of R positions taken by the opponent
		return Math.min(p1, p2);
	}

Topic 3: chess question:

Methods of violence:

public class JumpHorse{
    public static void main(String[] args) {
        int enda = 5;
        int endb = 7;
        int rest = 10;
        System.out.println(process(0, 0, enda, endb, rest));
    }

    public static int process(int x, int y, int enda, int endb, int rest) {
        if (x < 0 || x > 9 || y < 0 || y > 8) {
            return 0;
        }
        if (rest == 0) {
            return x == enda && y == endb ? 1 : 0;
        }
        int res = 0;
        res = process(x+2, y+1, enda, endb, rest-1) +
                process(x+1, y+2, enda, endb, rest-1) +
                process(x-1, y-2, enda, endb, rest-1) +
                process(x-2, y-1, enda, endb, rest-1) +
                process(x-1, y+2, enda, endb, rest-1) +
                process(x+1, y-2, enda, endb, rest-1) +
                process(x+2, y-1, enda, endb, rest-1) +
                process(x-2, y+1, enda, endb, rest-1);
        return res;
    }
}

Change to dynamic planning:

public class JumpHorse{
    public static void main(String[] args) {
        int enda = 5;
        int endb = 7;
        int rest = 10;
        System.out.println(waysdp(enda, endb, rest));
    }
    public static int waysdp(int a, int b, int s) {
        int[][][] dp = new int[10][9][s + 1];
        dp[a][b][0] = 1;
        for (int step = 1; step <= s; step++) { // By layer
            for (int i = 0; i < 10; i++) {
                for (int j = 0; j < 9; j++) {
                    dp[i][j][step] = getValue(dp, i - 2, j + 1, step - 1) + getValue(dp, i - 1, j + 2, step - 1)
                            + getValue(dp, i + 1, j + 2, step - 1) + getValue(dp, i + 2, j + 1, step - 1)
                            + getValue(dp, i + 2, j - 1, step - 1) + getValue(dp, i + 1, j - 2, step - 1)
                            + getValue(dp, i - 1, j - 2, step - 1) + getValue(dp, i - 2, j - 1, step - 1);
                }
            }
        }
        return dp[0][0][s];
    }
    // In the dp table, get the value of dp[i][j][step], but if the (I, j) position is out of bounds, return 0;
    public static int getValue(int[][][] dp, int i, int j, int step) {
        if (i < 0 || i > 9 || j < 0 || j > 8) {
            return 0;
        }
        return dp[i][j][step];
    }

}