Tree DP is the calculation of DP value on the data structure of the tree.

Tree DP has two directions: leaf - > root, root - > leaf.

Tree DP is implemented by memory search, so it is implemented by recursion.

Time complexity is generally O(n), and O(n*m) if there is dimension M.

1. The center of gravity of the tree: http://poj.org/problem?id=1655 Leaves - > Roots

The so-called center of gravity is that the size of each branch can be more uniform around the point, so the largest branch size is required to be the smallest.

After building the tree, DFS is performed once with any point as the root node, and the size of the subtree connected by all points is calculated.

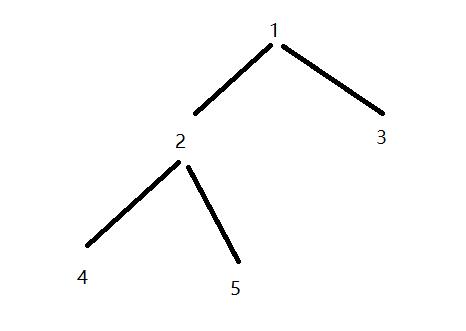
As shown in the following figure, DFS with 1 as the root yields {5, 3, 1, 1, 1}. Next, when calculating the size of a subtree rooted at any point, such as 2, it is only necessary to compare the size of 4, 5 directly connected by 2 and the size of the total number of n-nodes 2.

Look at the code.

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;

const int N=2e5+5;

int n;


struct node{               //Chain Forward Star Side
    int from;
    int to;
    int next;
}edge[2*N];
int head[N];
int cnt;
void add(int from,int to)
{
    cnt++;
    edge[cnt].from=from;
    edge[cnt].to=to;
    edge[cnt].next=head[from];
    head[from]=cnt;
}


int pre[N],sz[N];          //pre is used to record the parent node of a node, and sz is used to record the size of the subtree connected by a node.
int dfs(int p,int u)       //Random DFS with a point as its root
{
    pre[u]=p;    //Record parent node
    sz[u]=1;
    for(int i=head[u];i!=0;i=edge[i].next)    
    {
        int to = edge[i].to;
        if(to!=p) sz[u] += dfs(u, to);
    }
    return sz[u];
}


int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        cnt=0;
        memset(head,0,sizeof(head));
        memset(edge,0,sizeof(edge));
        memset(pre,0,sizeof(pre));
        memset(sz,0,sizeof(sz));
        scanf("%d",&n);
        for(int i=1;i<n;i++)
        {
            int x,y;
            scanf("%d%d",&x, &y);
            add(x,y);
            add(y,x);
        }
        dfs(0,1);

        int ansV=N;    //Record the maximum Balance and node number
        int ansO=N;
        for(int i=1;i<=n;i++)
        {
            int mx = n - sz[i];    //When i is the center, the only place where special judgment is needed is set to the maximum.

            for(int j=head[i];j!=0;j=edge[j].next)    //Next, compare the size of all directly connected subtrees of i
            {
                int to=edge[j].to;
                if(to!=pre[i]) mx = max(mx, sz[to]);
            }

            if(mx < ansV)    //The maximum balance with i as the center is obtained, which is smaller than the answer.
            {
                ansV = mx;
                ansO = i;
            }
        }
        printf("%d %d\n",ansO,ansV);
    }
}

2. A party without a supervisor: http://poj.org/problem?id=2342 Leaf - > Root

Simply put, it gives you a tree structure of a company. Everyone has a value of happiness. When a person appears, his immediate superior can not appear, and the total value of happiness is the largest.

Let dp[i][1] denote the maximum joy value when I appears, dp[i][0] denote the maximum joy value when I does not appear, and a[i] denote i's own joy value.

If u is the supervisor of v, there are dp[u][1] = a[u] + dp[v][0], dp[u][0] = max(dp[v][0], dp[v][1].

It can be renewed gradually from leaf to root.

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>

using namespace std;

const int N=6e3+5;

int n;
int dp[N][2],pre[N];    //pre stores a parent node at a certain point



int head[N],cnt;    //Chain Forward Star Side
struct nodes{
    int from;
    int to;
    int next;
}edge[N*2];


void Dfs(int node)
{
    for(int i=head[node];i!=0;i=edge[i].next)
    {
        int to=edge[i].to;
        Dfs(to);
        dp[node][1]+=dp[to][0];
        dp[node][0]+=max(dp[to][1],dp[to][0]);
    }
}


int main()
{
    while(cin>>n)
    {
        memset(dp,0,sizeof(dp));
        memset(pre,0,sizeof(pre));
        memset(head,0,sizeof(head));
        memset(edge,0,sizeof(edge));
        cnt=0;


        for(int i=1;i<=n;i++)
        {
            scanf("%d",&dp[i][1]);    //Direct deposit a[i] into dp[i][1]
        }

        int x,y;
        while(scanf("%d%d",&x,&y)!=-1)
        {
            if(x==0 && y==0) break;

            cnt++;                //Directed
            edge[cnt].from=y;
            edge[cnt].to=x;
            edge[cnt].next=head[y];
            head[y]=cnt;

            pre[x]=y;
        }

        int root;
        for(int i=1;i<=n;i++)    //Find the root node (the upper level of the root node is 0)
        {
            if(pre[i]==0)
            {
                root=i;
                break;
            }
        }
        Dfs(root);
        printf("%d\n",max(dp[root][0],dp[root][1]));
    }

}

To make a long story worse, I have seen a method that does not use direct violence to link forward star storage. To be honest, it can pass because this data is comparatively water. I tried to write it. It took 567 MS to run the data, while the gap is still very large when the chain forward star is only 78 Ms. This data is only 6 e3. But there's an unexpected gain from it. Look at the magic of if.

It is well known that if under the condition of &amp, the following judgment statement will not be executed when a current condition holds, so the first condition that can filter out more answers should be put in order to avoid the judgment that wastes time (as in the case of normal | | can be converted into &amp).

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>

using namespace std;

const int N=6e3+5;

int n;
int dp[N][2];
int pre[N];
bool vist[N];

void Dfs(int node)
{
    vist[node]=true;
    for(int i=1;i<=n;i++)
    {
        if(pre[i]==node && vist[i]==false)  //If two conditional switching positions in if are timed out directly
        {                                   //The first condition is to filter out more options.
            Dfs(i);
            dp[node][1]+=dp[i][0];
            dp[node][0]+=max(dp[i][0], dp[i][1]);
        }
    }
}

int main()
{
    while(cin>>n)
    {
        memset(dp,0,sizeof(dp));
        memset(pre,0,sizeof(pre));
        memset(vist,false,sizeof(vist));
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&dp[i][1]);
        }
        int x,y;
        while(scanf("%d%d",&x,&y)!=-1)
        {
            if(x==0 && y==0) break;
            pre[x]=y;
        }
        int root=0;
        for(int i=1;i<=n;i++)
        {
            if(pre[i]==0)
            {
                root=i;
                break;
            }
        }
        Dfs(root);
        printf("%d\n",max(dp[root][1],dp[root][0]));
    }
}

3. The furthest distance on the tree: http://acm.hdu.edu.cn/showproblem.php?pid=2196 Leaf - > Root - & Root - > Leaf

Simply put, there is a tree, each edge has a weight, to find the farthest distance each point can reach.

First, in a tree, for a point, the farthest distance can come from the direction of the parent node or the direction of the child node.

Let dp[i][1] be the farthest distance from I to the parent node, dp[i][0] the farthest distance from I to the child node, and pre[i] denote the parent node of I.

For the direction of the child node, let u be the parent of v, and dp[u][0] = max{dp[v][0] + w(u,v)} can be obtained from bottom to top by DFS.

For the direction of the parent node, let u and V be siblings with DP [u] [1] = w (u, pre [u]) + Max {dp [pre [u] [1], dp[v][0] + w(pre[u], v)}.

Intuitively speaking, that is, the farthest distance to the parent node = the maximum distance from the parent node to the parent node + (the parent node continues to go to the parent node | | the parent node goes to other sibling and child nodes). DFS from root to leaf is enough.

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>

using namespace std;

const int N=1e4+5;

int n;

int dp[N][2],prevs[N];


int head[N],cnt;        //Chain Forward Star Side
struct nodes{
    int from;
    int to;
    int value;
    int next;
}edge[2*N];

void Add(int x,int y,int v)
{
    cnt++;
    edge[cnt].from=x;
    edge[cnt].to=y;
    edge[cnt].value=v;
    edge[cnt].next=head[x];
    head[x]=cnt;
}




int Dfs(int node,int pre)        //Calculate the farthest distance to the child node
{
    for(int i=head[node];i!=0;i=edge[i].next)
    {
        int to=edge[i].to;
        if(to==pre) continue;
        int value=edge[i].value;
        prevs[to]=node;
        dp[node][0]=max(dp[node][0],value+Dfs(to,node));
    }
    return dp[node][0];
}



void Dfs2(int node,int pre)       //Calculate the farthest distance to the parent node
{
    int v=0;               //Record the distance from this point to the parent node
    dp[node][1]=dp[pre][1];    //Judgment of Mixing Parent Node and Brother Node

    for(int i=head[pre];i!=0;i=edge[i].next)    //Take out all the brothers and compare them to see where the parent node should go next.
    {
        int to=edge[i].to;
        if(to==prevs[pre]) continue;
        int value=edge[i].value;
        if(to==node) v=value;
        else dp[node][1]=max(dp[node][1], dp[to][0]+value);
    }


    dp[node][1]+=v;          //After selecting the next step of the parent node, add the distance from the parent node to the parent node.

    for(int i=head[node];i!=0;i=edge[i].next)
    {
        int to=edge[i].to;
        if(to!=pre) Dfs2(to,node);
    }
}


void Origin()    //Initialization function
{
    memset(prevs,0,sizeof(prevs));
    memset(dp,0,sizeof(dp));
    memset(head,0,sizeof(head));
    cnt=0;
    memset(edge,0,sizeof(edge));
}


int main()
{
    while(cin>>n)
    {
        Origin();
        int p,v;
        for(int i=1;i<n;i++)
        {
            scanf("%d%d",&p,&v);
            Add(i+1,p,v);
            Add(p,i+1,v);
        }
        Dfs(1,0);
        Dfs2(1,0);
        for(int i=1;i<=n;i++)
        {
            printf("%d\n",max(dp[i][0], dp[i][1]));
        }
    }
}

1. Godfather: http://poj.org/problem?id=3107

The expansion of the problem of tree's center of gravity.

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;

const int N=5e4+5;

int n;

int mxOfNode[N];

int head[N],cnt=0;
struct node{
    int from;
    int to;
    int next;
}edge[2*N];

void Add(int x,int y)
{
    cnt++;
    edge[cnt].from=x;
    edge[cnt].to=y;
    edge[cnt].next=head[x];
    head[x]=cnt;
}


int pre[N],sz[N];

int Dfs(int prev,int node)
{
    pre[node]=prev;
    sz[node]=1;
    for(int i=head[node];i!=0;i=edge[i].next)
    {
        int to=edge[i].to;
        if(to!=prev) sz[node] += Dfs(node,to);
    }
    return sz[node];
}



int main()
{
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        Add(x,y);
        Add(y,x);
    }
    Dfs(0,1);

    int ansV=N;
    for(int i=1;i<=n;i++)
    {
        int mx = n-sz[i];
        for(int j=head[i];j!=0;j=edge[j].next)
        {
            int to=edge[j].to;
            if(to!=pre[i]) mx = max(mx,sz[to]);
        }
        mxOfNode[i]=mx;
        if(mx<=ansV)
        {
            ansV=mx;
        }
    }
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        if(mxOfNode[i]==ansV)
        {
            if(cnt==0) printf("%d",i);
            else printf(" %d",i);
            cnt=1;
        }
    }
    printf("\n");

}

2. The more, The Better: http://acm.hdu.edu.cn/showproblem.php?pid=1561

Knapsack Tree DP

The node that can be conquered first is regarded as the parent node to form a tree, which forms a forest.

Because the parent node in the question is zero, we can regard all the trees in the forest as the parent node of 0, so that the forest becomes a tree.

Let dp[i][j] denote the maximum value of taking J nodes from the first node.

Let u be the parent of v, with DP [u] [j] = max (dp [u] [j], DP [u] [k] + DP [v] [j-k])

Update from bottom to top.

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>

using namespace std;

const int N=205;

int n,m;

int head[N],cnt;
struct nodes{
    int from;
    int to;
    int next;
}edge[2*N];

int dp[N][N];
bool vist[N];

void Origin()
{
    memset(head,0,sizeof(head));
    cnt=0;
    memset(edge,0,sizeof(edge));
    memset(dp,0,sizeof(dp));
    memset(vist,false,sizeof(vist));
}

void Dfs(int node)
{
    vist[node]=true;
    for(int i=head[node];i!=0;i=edge[i].next)
    {
        int to=edge[i].to;
        if(vist[to]==false) Dfs(to);
        for(int j=m;j>=2;j--)
        {
            for(int k=1;k<j;k++)
            {
                dp[node][j]=max(dp[node][j],dp[node][k]+dp[to][j-k]);
            }
        }


    }
}

int main()
{
    while(cin>>n>>m)
    {
        Origin();
        if(n==0 && m==0) break;
        int x,y;
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d",&x,&y);

            cnt++;                //one-way
            edge[cnt].from=x;
            edge[cnt].to=i;
            edge[cnt].next=head[x];
            head[x]=cnt;

            dp[i][1]=y;
        }
        m++;    //Because we have virtually a number of zero nodes
        Dfs(0);
        printf("%d\n",dp[0][m]);
    }
}