Logistic chaos scrambling, not to mention how complex, is actually very simple.

Logistic function is a dynamic system derived from population statistics, and its system equation form is as follows:

 X(k+1) = u * X(k) * [1 - X(k)],(k=0,1,...,n)

Don't worry about how you get this equation first. If you feel uncomfortable, go to Baidu yourself. It can be seen that this equation is nonlinear and iterative. To use, we need to know two things:

① Initial value: X(0)

② Parameter: u

Why can this equation be called chaos? When is it a chaotic system? This is also conditional:

①    0  < X(0) < 1

②   3.5699456...  <  u <=4

When the above two conditions are satisfied, the Logistic function works in a chaotic state. How did these two conditions come? Please Baidu. We only talk about algorithm and implementation here. What is chaos: as the name suggests, it is a disordered, unpredictable, chaotic, untouchable state. What happens in chaotic state? Let's take the following parameters as an example:

①    X(0) = 0.1

②    u = 4

After n iterations, we get n values such as X(1), X(2),..., X(n). Then this is A chaotic sequence, which is one-dimensional, temporarily called sequence A, that is, the sequence we want to get. In MATLAB, it can be seen that the value of X(i) (i=1,2,..., n) is between (0,1) - this is A good characteristic, just like the gray value of the image is between (0255). Then we normalize the one-dimensional sequence to (0255) to obtain sequence B.

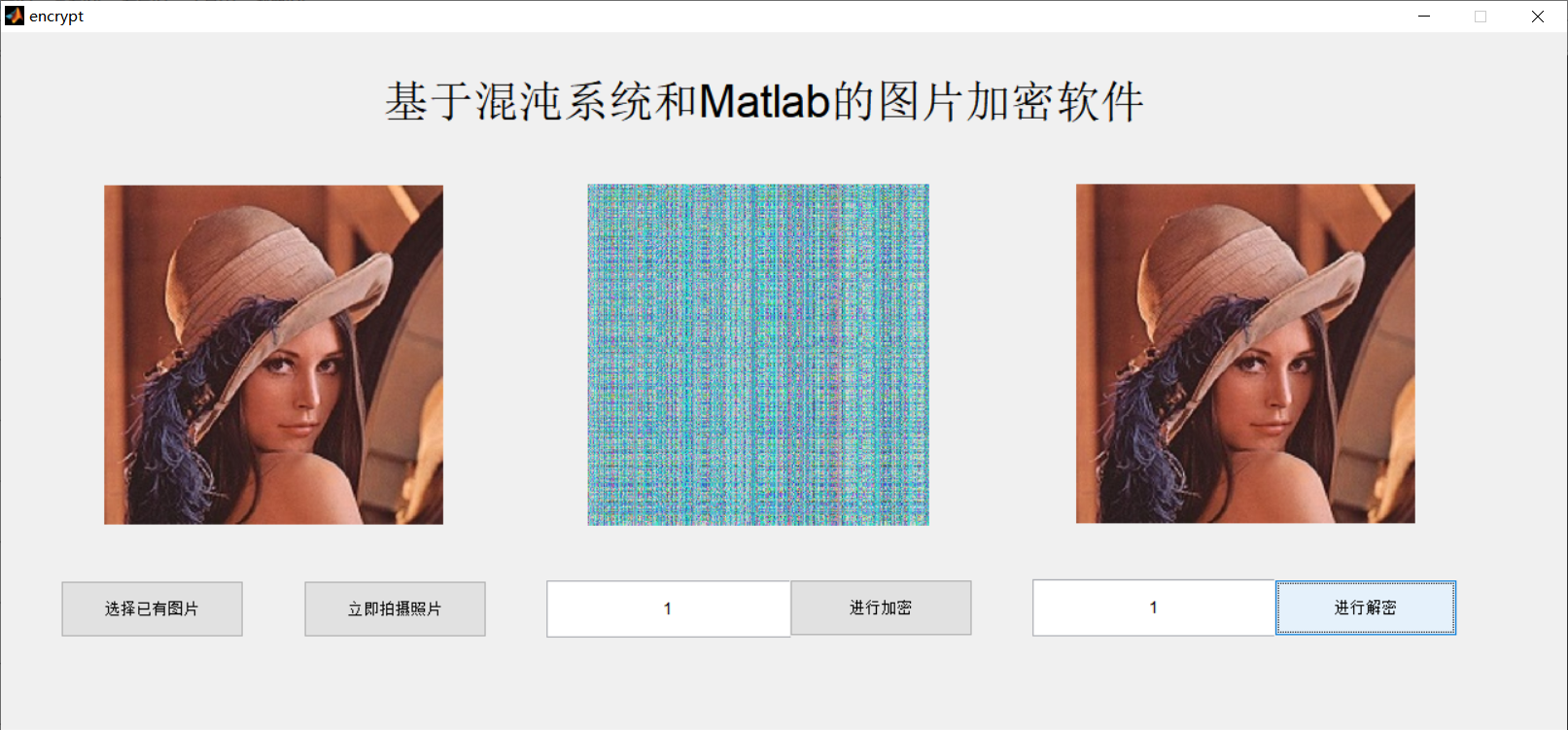
Let's look at the encryption process. For an image of M*N size (temporarily called Picture), we need to generate A matrix of the same size to encrypt it. In this way, we only need to iterate M*N times to get sequence A, and then turn it into sequence B. at this time, sequence B is one-dimensional, and turn it into A two-dimensional matrix of M*N (hereinafter referred to as Fuck). Therefore, A new image called Rod can be obtained by XOR between Fuck and Picutre. In this way, an image encryption is completed, and the encrypted image is Rod.

Rod=Picture ⊕ future (⊕ indicates XOR)

So the secret key in our hands is: u, X(0)

This encryption method is called sequence encryption. It can be seen that this encryption method changes the gray level of the lower pixel (the histogram changes) without changing the position. The same principle for decryption: Picture = Rod ⊕ future.

function varargout = encrypt(varargin)
% ENCRYPT MATLAB code for encrypt.fig
%      ENCRYPT, by itself, creates a new ENCRYPT or raises the existing
%      singleton*.
%
%      H = ENCRYPT returns the handle to a new ENCRYPT or the handle to
%      the existing singleton*.
%
%      ENCRYPT('CALLBACK',hObject,eventData,handles,...) calls the local
%      function named CALLBACK in ENCRYPT.M with the given input arguments.
%
%      ENCRYPT('Property','Value',...) creates a new ENCRYPT or raises the
%      existing singleton*.  Starting from the left, property value pairs are
%      applied to the GUI before encrypt_OpeningFcn gets called.  An
%      unrecognized property name or invalid value makes property application
%      stop.  All inputs are passed to encrypt_OpeningFcn via varargin.
%
%      *See GUI Options on GUIDE's Tools menu.  Choose "GUI allows only one
%      instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help encrypt

% Last Modified by GUIDE v2.5 24-Dec-2019 21:56:19

% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',       mfilename, ...
                   'gui_Singleton',  gui_Singleton, ...
                   'gui_OpeningFcn', @encrypt_OpeningFcn, ...
                   'gui_OutputFcn',  @encrypt_OutputFcn, ...
                   'gui_LayoutFcn',  [] , ...
                   'gui_Callback',   []);
if nargin && ischar(varargin{1})
    gui_State.gui_Callback = str2func(varargin{1});
end

if nargout
    [varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
    gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT


% --- Executes just before encrypt is made visible.
function encrypt_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
% varargin   command line arguments to encrypt (see VARARGIN)

% Choose default command line output for encrypt
handles.output = hObject;

% Update handles structure
guidata(hObject, handles);

% UIWAIT makes encrypt wait for user response (see UIRESUME)
% uiwait(handles.figure1);


% --- Outputs from this function are returned to the command line.
function varargout = encrypt_OutputFcn(hObject, eventdata, handles) 
% varargout  cell array for returning output args (see VARARGOUT);
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout{1} = handles.output;


% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
[filename,filepath] = uigetfile({'*.bmp;*.jpg;*.png;*.jpeg;*.tif','file type (*.bmp,*.jpg,*.png,*.jpeg,*.tif)';'*.*', 'All documents(*.*)'},'Pick an image');
file = strcat(filepath,filename);
im = imread(file);
axes(handles.axes1);
imshow(im);
imwrite(im,'snap.bmp'); 



% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton2 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
obj = videoinput('winvideo',1,'YUY2_1280x720')%1280x720 160x120 176x144 320x240 352x288 640x480 
% vidRes = get(obj, 'VideoResolution');
% nBands = get(obj, 'NumberOfBands');
% preview(obj);%getsnapshot(obj);
vidRes = get(obj, 'VideoResolution');
nBands = get(obj, 'NumberOfBands');
hImage = image( zeros(vidRes(2), vidRes(1), nBands),'parent',handles.axes1);
preview(obj, hImage);
frame = getsnapshot(obj);
frame = ycbcr2rgb(frame);
imwrite(frame,'snap.bmp','bmp');
pic = imread('snap.bmp');
axes(handles.axes1);
imshow(pic);
title(date,'color','r');



function edit1_Callback(hObject, eventdata, handles)
% hObject    handle to edit1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: get(hObject,'String') returns contents of edit1 as text
%        str2double(get(hObject,'String')) returns contents of edit1 as a double
% input = str2num(get(hObject,'String'));%here get Pay attention later
% if(isempty(input))
%     set(hObject,'String','0')
% end
guidata(hObject,handles)


% --- Executes during object creation, after setting all properties.
function edit1_CreateFcn(hObject, eventdata, handles)
% hObject    handle to edit1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end


% --- Executes on button press in pushbutton3.
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton3 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
a=imread('snap.bmp');
R=a(:,:,1);                           %Take image R Layer pixel
G=a(:,:,2);                           %Take image G Layer pixel
B=a(:,:,3);                           %Take image B Layer pixel
[M1,N1]=size(R);
[M2,N2]=size(G);
[M3,N3]=size(B);
h=0.01;    %Chaotic sequence initialization 
x=zeros(1,40001);x(1)= str2num(get(handles.edit1,'String')); 
y=zeros(1,40001);y(1)=0; 
z=zeros(1,40001);z(1)=0; 
w=zeros(1,40001);w(1)=0; 
v=zeros(1,40001);v(1)=0; 
for n=1:40000         %Generating chaotic sequence initialization,Euler method 
  x(n+1)=x(n)+h*(3.5*(y(n)-x(n)-(-1.2+0.3*(w(n)*w(n)))*x(n))); 
  y(n+1)=y(n)+h*(2.1*y(n)-z(n)-0.2*(y(n)-x(n))-0.2*(1.2+7*abs(v(n)))*y(n)); 
  z(n+1)=z(n)+h*(2.1*y(n)-z(n));
  w(n+1)=w(n)+h*(x(n));
  v(n+1)=v(n)+h*(y(n)); 
end 
for n=1:40000  %Three sequences were improved 
    x(n)=x(n)*1000000-round(x(n)*1000000); 
    y(n)=y(n)*1000000-round(y(n)*1000000); 
    z(n)=z(n)*1000000-round(z(n)*1000000);
    w(n)=w(n)*1000000-round(w(n)*1000000); 
    v(n)=v(n)*1000000-round(v(n)*1000000); 
end 

% %yes R Channel encryption

for j=1:N1  %Scrambling pixels with bit XOR method 
    aa=(uint8((M1*N1*(x(N1+j)+0.5))*ones(M1,1))); 
    g1(:,j)=bitxor(R(:,j),aa); 
    h1(:,j)=bitxor(g1(:,j),aa); %Decrypt pixel scrambling 
end 
for i=1:M1 %Row scrambling
    t(1:N1)=y(1:N1);
    [t1,index1]=sort(t(1:N1));
    t1=flipud(t1);
    g2(i,:)=g1(i,index1);
    h2(i,index1)=g2(i,:);
end
for j=1:N1 %Column scrambling
    t(1:M1)=z(1:M1);
    [t1,index1]=sort(t(1:M1));
    index1=flipud(index1);
    g3(:,j)=g2(index1,j);
    h3(index1,j)=g3(:,j);
end

% %yes G Channel encryption

for j=1:N2  %Scrambling pixels with bit XOR method 
    bb=(uint8((M2*N2*(x(N2+j)+0.5))*ones(M2,1))); 
    j1(:,j)=bitxor(G(:,j),bb); 
    k1(:,j)=bitxor(j1(:,j),bb); %Decrypt pixel scrambling 
end 
for i=1:M2 %Row scrambling
    t(1:N2)=x(1:N2);
    [t2,index2]=sort(t(1:N2));
    t2=flipud(t2);
    j2(i,:)=j1(i,index2);
    k2(i,index2)=j2(i,:);
end

​