Introduction to g2o Library

g2o(General Graphic Optimization, G 2 O G^2O G2O) is an open source C + + framework for solving nonlinear least squares problems based on graph optimization.

Github home page: https://github.com/RainerKuemmerle/g2o

The core classes of the library are as follows:

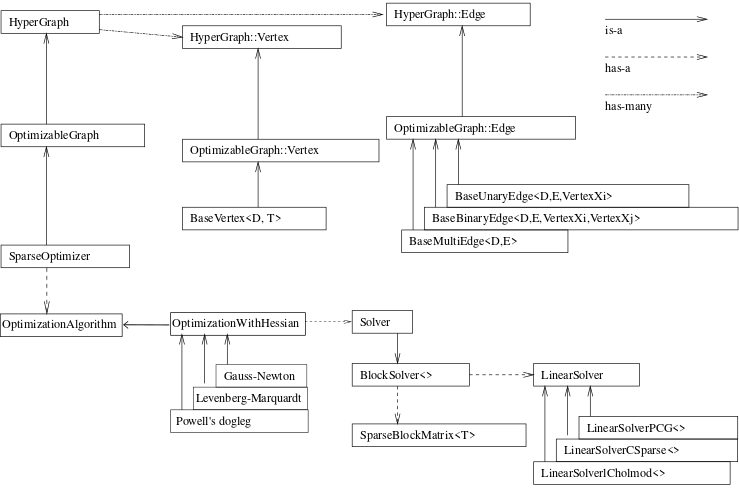
Graph optimization theory

For the basic theory of graph theory, please refer to another blog post of the blogger: u graph theory and graph search algorithm Learn about the relevant contents of the diagram in.

It should be noted that in g2o, vertices are used to represent nodes, which are the same object.

If nodes are used to represent optimization variables and edges are used to represent error terms, a nonlinear least squares problem can be described as a graph structure. If the definition of probability graph is adopted here, it can be called Bayesian graph or factor graph.

As shown in the following figure, the camera motion pose is constructed. In the figure, circular nodes are used to represent road markings; The camera pose is represented by triangular nodes; The camera motion model is represented by the implementation edge; The observation model is represented by dotted line:

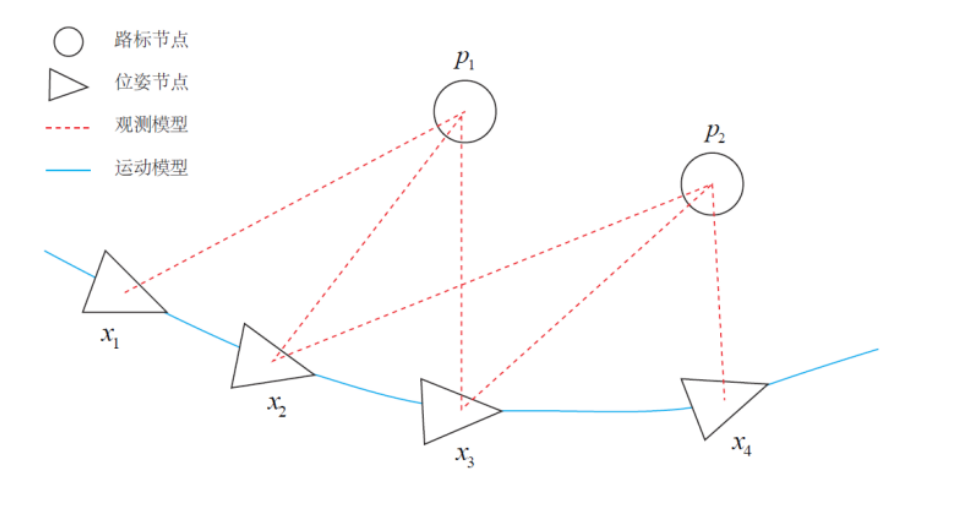
Generally, isolated nodes can be removed in advance and nodes with more edges (i.e. larger degrees) can be optimized first.

g2o compilation and installation

First, download the source code of the g2o Library:

git clone https://github.com/RainerKuemmerle/g2o

Secondly, install dependencies. Some dependencies have been completed during the installation of Ceres Library:

sudo apt install -y qt5-qmake qt5-default libqglviewer-dev-qt5 libsuitesparse-dev libcxsparse3 libcholmod3

Then, enter the source code directory for compilation:

# New compilation directory
cd g2o && mkdir build && cd build
# compile
cmake ..
make -j12

After compilation, install the generated library file:

# install
sudo make install

The default installation location is as follows:

# include 
/usr/local/g2o
# lib
/usr/local/lib/

Engineering configuration

Clion + Ubuntu 20 is still used 04 development and new project Study.

engineering structure

The structure is as follows:

.
├── CMakeLists.txt
├── include
│   └── main.h
└── src
    ├── CMakeLists.txt
    └── main.cpp

The subdirectory include is used to store header files; The subdirectory src is used to store the source code

CMake configuration

Cmakelists. In the root directory Txt file is as follows:

# cmake version
cmake_minimum_required(VERSION 3.21)
# project name
project(Study)
# cpp version
set(CMAKE_CXX_STANDARD 14)
# eigen
include_directories("/usr/include/eigen3")
# g2o
find_package(g2o REQUIRED)
include_directories(${g2o_INCLUDE_DIRS})
# opencv
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
# incldue
include_directories(include)
# src
add_subdirectory(src)

Cmakelists. In the src directory Txt file is as follows:

# exec
add_executable(Study main.cpp)
# link opencv
target_link_libraries(Study ${OpenCV_LIBS})
# link g2o
target_link_libraries(Study g2o_core g2o_stuff)

Note here that blogger target_ link_ If the libraries section is directly linked to ${g2o_LIBRARIES}, an error will be reported as follows:

undefined reference to g2o::xxxxxxxx

That is, the library file is not linked successfully, so the corresponding library file is directly linked.

Header file configuration

Header file main. In the include directory H contents are as follows:

#ifndef STUDY_MAIN_H
#define STUDY_MAIN_H

#include <iostream>
#include <cmath>
#include <chrono>
//  Eigen
#include <Eigen/Core>
//  OpenCV
#include <opencv2/opencv.hpp>
//  g2o
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>

//  namespace
using namespace std;
using namespace Eigen;


#endif //STUDY_MAIN_H

The Eigen library is mainly imported for matrix data representation, Opencv library is used for random number generation, and g2o library is used for nonlinear least squares solution of graph optimization.

source file

src source file main The initial contents of CPP are as follows:

#include "main.h"

int main()
{

    return 0;
}

g2o library API

Using g2o library for graph optimization mainly includes the following steps:

• Define the types of nodes and edges in the graph
• Construction diagram structure
• Selected optimization algorithm
• Optimize and get results

Curve fitting problem

Here, we still take the handwritten Gauss Newton method as an example to learn the use of g2o library. For the description of the problem, see the problem description as follows: Construction of curve fitting model

Firstly, the curve fitting problem is constructed as a graph, with nodes representing the optimization variables and edges representing the error terms:

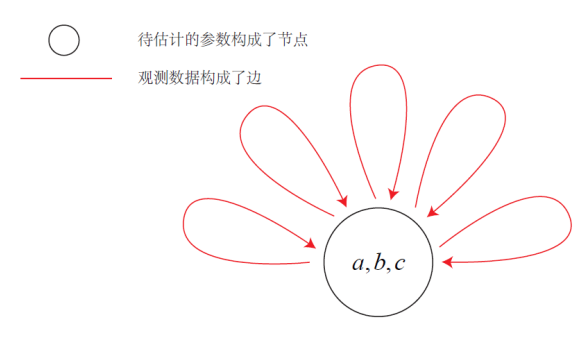
In the curve fitting problem, the variables to be optimized are the parameters of the curve model: a , b , c a,b,c a. b, c, the error term is a group of data containing noise.

Definition of node class

Node class inherits from g2o:: basevertex < int d, typename T >

• int D: Dimension of optimization variable
• typename T: data type of optimization variable

For example, build an optimization variable node class of three-dimensional Eigen::Vector3d type:

class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {}

The name of the derived class defined here is CurveFittingVertex.

For the definition of nodes, you also need to rewrite several virtual functions.

Reset function

Class is used to optimize variables_ Initialize with the value of estimate.

As the following reset function, initialize the three-dimensional optimization variable to 0:

virtual void setToOriginImpl() override
{
    _estimate << 0, 0, 0;
}

Update function

The member function oplusImpl(const double *update) of class is used to define the method of node update, that is, it is used for processing x k + 1 = x k + Δ x x_{k+1}=x_k+\Delta x xk+1​=xk​+ Δ The process of x.

• const double *update: pointer data, update quantity

It should be noted that for variables representing different uses, incremental updates are calculated in different ways. For example, the curve fitting problem only needs to be updated by simple addition:

virtual void oplusImpl(const double *update) override
    {
        _estimate += Vector3d(update);
    }

For example, for the updating of camera pose, the perturbation model of Lie group can be used for updating (left multiplication perturbation, right multiplication perturbation)

Save and read functions

Class member functions read (istream & in) and write (istream & out) are used to save and read disks.

virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}

Node definition of curve fitting problem

For the above curve fitting problem, the node is defined as follows:

//  Node class, the optimization variable is 3D, and the data of Eigen::Vector3d type
class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {
public:
    //  alignment
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    //  Reset function
    virtual void setToOriginImpl() override {
        _estimate << 0, 0, 0;
    }

    //  Update function
    virtual void oplusImpl(const double *update) override {
        _estimate += Vector3d(update);
    }

    //  Disk reading function and disk saving function: leave blank and not use for the time being
    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}
    
};

Gen member variable_ MAKE_ ALIGNED_ OPERATOR_ The new declaration solves the alignment problem when creating a new object of this type.

Definition of edge class

Edge classes inherit different classes according to whether the nodes linked by the edge are one or two.

The unary edge problem inherits from the class g2o:: baseunaryedge < int d, typename e, typename vertexxi >

• int D: Dimension of error item
• typename E: data type of error item
• typename VertexXi: node type of edge link

Binary edge problem inherits from class g2o:: basebinaryedge < int d, typename e, typename vertexxi, typename vertexj >

• int D: Dimension of error item
• typename E: data type of error item
• typename VertexXi: the type of the first node of the edge link
• typename VertexXj: the type of the second node of the edge link

For example, for the curve fitting problem, a one-dimensional double type metaclass should be constructed, and the linked node type is CurveFittingVertex:

class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {}

The name of the derived class defined here is CurveFittingEdge.

Similarly, for the definition of edge, you also need to rewrite several virtual functions.

Constructor

When an edge class is instantiated, the corresponding feature needs to be passed in x x x. Use private members of classes_ X accepted:

CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}

In g2o, private members are used_ measurement stores observation data y y y

Error calculation function

Class is used to define the error calculation function of the edge. The error function is mainly used to obtain the value of the link node and calculate the corresponding residual value.

For example, the error function of curve fitting is as follows:

virtual void computeError() override {
    //  Get node
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    //  Gets the optimization variable (node value) of the node
    const Eigen::Vector3d abc = v->estimate();
    //  Calculation error value
    _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}

In the curve fitting problem, the optimization variable is a three-dimensional vector, corresponding to curve parameters: A, b, c, and the corresponding error calculation formula is as follows:
e r r o r = y − e x p ( a x 2 + b x + c ) error = y-exp(ax^2+bx+c) error=y−exp(ax2+bx+c)
Where y is the observation data, and the calculated error value error is used to calculate the derivative.

Jacobian calculation function

Class is used to define the Jacobian calculation function of the edge. Similarly, the Jacobian calculation function obtains the values of the edge linked nodes and their corresponding optimization variables, so as to solve the value of the Jacobian matrix.

For example, the Jacobian calculation function of curve fitting problem is as follows:

virtual void linearizeOplus() override {
    //  Get node
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    //  Gets the optimization variable (node value) of the node
    const Eigen::Vector3d abc = v->estimate();
    //  Jacobian matrix solution
    double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
    _jacobianOplusXi[0] = -_x * _x * y;
    _jacobianOplusXi[1] = -_x * y;
    _jacobianOplusXi[2] = -y;
}

Note here that for the univariate edge problem, only calculation is required_ jacobianOplusXi;

For the binary boundary problem, it should be calculated at the same time_ jacobianOplusXi and_ The value of jacobianOplusXj.

Save and read functions

Class member functions read (istream & in) and write (istream & out) are used to save and read disks.

virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}

Edge definition of curve fitting problem

For the above curve fitting problem, the definition of edge is as follows:

//  Edge class, the error item is 1-dimensional double type data, and the node type of edge link is CurveFittingVertex type
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
    //  alignment
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    //  Constructor
    CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}

    //  Calculation of edge function error
    virtual void computeError() override {
        //  Get node
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //  Gets the optimization variable (node value) of the node
        const Eigen::Vector3d abc = v->estimate();
        //  Calculate residual value
        _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
    }

    //  Jacobian calculation function of edge
    virtual void linearizeOplus() override {
        //  Get node
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //  Gets the optimization variable (node value) of the node
        const Eigen::Vector3d abc = v->estimate();
        //  Derivation
        double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
        _jacobianOplusXi[0] = -_x * _x * y;
        _jacobianOplusXi[1] = -_x * y;
        _jacobianOplusXi[2] = -y;
    }

    //  Disk reading function and disk saving function: leave blank and not use for the time being
    virtual bool read(istream &in) {}
    virtual bool write(ostream &out) const {}

private:
    double _x;  // x value, y value is_ measurement

};

Gen member variable_ MAKE_ ALIGNED_ OPERATOR_ The new declaration solves the alignment problem when creating a new object of this type.

Curve fitting data generation

After completing the construction of node and edge types, first generate the data used in the main function:

int main()
{
    /*--------  Initial parameter configuration--------*/
    //  Actual curve parameters
    double ar = 1.0, br = 1.0, cr = 1.0;
    //  Initial value of estimated curve parameters
    double ae = 2.0, be = 1.0, ce = 5.0;
    //  Number of sampling observation data points
    int N = 100;
    //  Noise standard deviation and its reciprocal
    double w_sigma = 1.0;
    //  Random number generator
    cv::RNG rng;

    /*--------  Observation data generation--------*/
    vector<double> x_data, y_data;
    for(int i = 0; i < N; i++){
        double x = i / 100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar * x * x +br * x + cr) + rng.gaussian(w_sigma * w_sigma));
    }
    
    return 0;
}

Build optimizer

After the initial data is generated, the configuration of the graph model can be built in the main function.

Linear solver, error block

Firstly, the types of linear solver and error block in the problem are defined. Here, the optimization variable of curve fitting problem is three-dimensional, and the error term is one-dimensional:

//  Type of error item: the optimization variable dimension of error item is 3 and the value dimension of error item is 1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
//  Type of Solver: solve using LinearSolverDense
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;

The types of linear solvers are LinearSolverDense, LinearSolverPCG, linearsolvercparse, LinearSolverCholmod

Gradient descent method

Then, set the gradient descent method:

auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

GN method is selected here, including GN method, LM method and DogLeg method. The corresponding API s are as follows:

• GN method

  g2o::OptimizationAlgorithmGaussNewton(std::unique_ptr<Solver> solver);
  

• LM method

  g2o::OptimizationAlgorithmLevenberg(std::unique_ptr<Solver> solver);
  

• DogLeg method

  g2o::OptimizationAlgorithmDogleg(std::unique_ptr<BlockSolverBase> solver);
  

Curve fitting problem optimizer

The optimizer of curve fitting problem is constructed as follows:

//  Type of error item: the optimization variable dimension of error item is 3 and the value dimension of error item is 1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
//  Type of linear solver: solve using LinearSolverDense
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
//  Optimizer: GN method is used to solve the setting
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

Graph model establishment

Set optimizer

First, build a graph model and set up the optimizer

//  Graph model
g2o::SparseOptimizer optimizer;
//  Set optimizer
optimizer.setAlgorithm(solver);
//  Open debug output
optimizer.setVerbose(true);

Add node

Add nodes to the built graph model:

//  Instantiation node type
CurveFittingVertex *v = new CurveFittingVertex();
//  Optimization variable initialization
v->setEstimate(Eigen::Vector3d(ae, be, ce));
//  Set node id in the diagram
v->setId(0);
//  Add nodes to graph model
optimizer.addVertex(v);

Add edge

Fill the generated data points into the edge one by one by traversal:

for (int i = 0; i < N; i++)
{
    //  Instanced edge type, incoming feature x
    CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
    //  Set the edge id in the drawing
    edge->setId(i);
    //  Set connected nodes: node number and node object
    edge->setVertex(0, v);
    //  Set observation data
    edge->setMeasurement(y_data[i]);
    //  Setting information matrix: inverse of covariance matrix
    edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
    //  Add edges to graph model
    optimizer.addEdge(edge);
}

Start optimization

Finally, start to solve the optimization problem:

/*--------  Figure optimization start--------*/
cout << "start optimization" << endl;
//  Initialization optimization
optimizer.initializeOptimization();
//  Optimization times setting
optimizer.optimize(10);
//  Output optimization value
Eigen::Vector3d abc_estimate = v->estimate();

Example: curve fitting

code

The complete code is as follows:

#include "main.h"

//  Node class, the optimization variable is 3D, and the data of Eigen::Vector3d type
class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {
public:
    //  alignment
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    //  Reset function
    virtual void setToOriginImpl() override {
        _estimate << 0, 0, 0;
    }

    //  Update function
    virtual void oplusImpl(const double *update) override {
        _estimate += Vector3d(update);
    }

    //  Disk reading function and disk saving function: leave blank and not use for the time being
    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}

};

//  Edge class, the error item is 1-dimensional double type data, and the node type of edge link is CurveFittingVertex type
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
    //  alignment
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    //  Constructor
    CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}

    //  Error calculation function of edge
    virtual void computeError() override {
        //  Get node
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //  Gets the optimization variable (node value) of the node
        const Eigen::Vector3d abc = v->estimate();
        //  Calculate residual value
        _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
    }

    //  Jacobian calculation function of edge
    virtual void linearizeOplus() override {
        //  Get node
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //  Gets the optimization variable (node value) of the node
        const Eigen::Vector3d abc = v->estimate();
        //  Derivation
        double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
        _jacobianOplusXi[0] = -_x * _x * y;
        _jacobianOplusXi[1] = -_x * y;
        _jacobianOplusXi[2] = -y;
    }

    //  Disk reading function and disk saving function: leave blank and not use for the time being
    virtual bool read(istream &in) {}

    virtual bool write(ostream &out) const {}

private:
    double _x;  // x value, y value is_ measurement

};

int main()
{
    /*--------  Initial parameter configuration--------*/
    //  Actual curve parameters
    double ar = 1.0, br = 1.0, cr = 1.0;
    //  Initial value of estimated curve parameters
    double ae = 2.0, be = 1.0, ce = 5.0;
    //  Number of sampling observation data points
    int N = 100;
    //  Noise standard deviation and its reciprocal
    double w_sigma = 1.0;
    //  Random number generator
    cv::RNG rng;

    /*--------  Observation data generation--------*/
    vector<double> x_data, y_data;
    for(int i = 0; i < N; i++){
        double x = i / 100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar * x * x +br * x + cr) + rng.gaussian(w_sigma * w_sigma));
    }

    /*--------  Optimizer configuration--------*/
    //  Type of error item: the optimization variable dimension of error item is 3 and the value dimension of error item is 1
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
    //  Type of linear solver: solve using LinearSolverDense
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
    //  Optimizer: GN method is used to solve the setting
    auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

    /*--------  Figure model configuration--------*/
    //  Graph model
    g2o::SparseOptimizer optimizer;
    //  Set optimizer
    optimizer.setAlgorithm(solver);
    //  Open debug output
    optimizer.setVerbose(true);

    //  Instantiation node type
    CurveFittingVertex *v = new CurveFittingVertex();
    //  Optimization variable initialization
    v->setEstimate(Eigen::Vector3d(ae, be, ce));
    //  Set the node id in the diagram
    v->setId(0);
    //  Add nodes to graph model
    optimizer.addVertex(v);

    //  Adding edges to a graph model
    for (int i = 0; i < N; i++)
    {
        //  Instanced edge type, incoming feature x
        CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
        //  Set the edge id in the drawing
        edge->setId(i);
        //  Set connected nodes: node number and node object
        edge->setVertex(0, v);
        //  Set observation data
        edge->setMeasurement(y_data[i]);
        //  Setting information matrix: inverse of covariance matrix
        edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
        //  Add edges to graph model
        optimizer.addEdge(edge);
    }

    /*--------  Figure optimization start--------*/
    cout << "start optimization" << endl;
    //  Solve start timing t1
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    //  Initialization optimization
    optimizer.initializeOptimization();
    //  Optimization times setting
    optimizer.optimize(10);
    //  Solution end timing t2
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    //  Total solution time
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

    //  Output optimization value
    Eigen::Vector3d abc_estimate = v->estimate();
    cout << "estimated model: " << abc_estimate.transpose() << endl;

    return 0;
}

output

The output results are as follows:

start optimization
solve time cost = 0.00741664 seconds. 
estimated model: 0.877649  1.21235 0.931272
iteration= 0	 chi2= 12378200.264531	 time= 0.000666326	 cumTime= 0.000666326	 edges= 100	 schur= 0
iteration= 1	 chi2= 1618271.477542	 time= 0.000780621	 cumTime= 0.00144695	 edges= 100	 schur= 0
iteration= 2	 chi2= 199423.333138	 time= 0.000621562	 cumTime= 0.00206851	 edges= 100	 schur= 0
iteration= 3	 chi2= 20992.691489	 time= 0.000643664	 cumTime= 0.00271217	 edges= 100	 schur= 0
iteration= 4	 chi2= 1519.455061	 time= 0.000571236	 cumTime= 0.00328341	 edges= 100	 schur= 0
iteration= 5	 chi2= 132.709242	 time= 0.000571791	 cumTime= 0.0038552	 edges= 100	 schur= 0
iteration= 6	 chi2= 102.041451	 time= 0.000593103	 cumTime= 0.0044483	 edges= 100	 schur= 0
iteration= 7	 chi2= 102.004182	 time= 0.000571012	 cumTime= 0.00501932	 edges= 100	 schur= 0
iteration= 8	 chi2= 102.004182	 time= 0.000571102	 cumTime= 0.00559042	 edges= 100	 schur= 0
iteration= 9	 chi2= 102.004182	 time= 0.000571705	 cumTime= 0.00616212	 edges= 100	 schur= 0