1, Introduction

1 purpose of digital image scrambling

So far, the more mature information hiding algorithms basically take the image as the carrier. Image scrambling, as the name suggests, is to disrupt the image and hide the real content of the original image. Digital image scrambling is similar to the idea of information file encryption. It mainly "disturbs" the image by changing the pixel position of the digital image, making it beyond recognition and disorderly, so as to hide the real information to be expressed by the image. Image scrambling can achieve two purposes:

1.1 encryption processing
Image scrambling transformation is a content-based image encryption method. Like decrypting the encrypted information without knowing the key, it is also difficult to recover the information of the original image without knowing the algorithm used for image scrambling.

1.2 enhance the robustness of image camouflage (robustness: it refers to that the digital watermark can still maintain partial integrity and be accurately identified after going through a variety of unintentional or intentional signal processing processes. Possible signal processing processes include channel noise, filtering, D / A and a / D conversion, resampling, shearing, displacement, scale change and lossy compression coding. It is mainly used for copyright protection (Fragile Watermarking), which is mainly used for integrity protection. This kind of watermark also embeds invisible information in content data. When the content changes, the watermark information will change accordingly, so that it can identify whether the original data has been tampered with.)

As a preprocessing method of information hiding, scrambling technology can greatly enhance the robustness of image information camouflage. It is mainly reflected in three aspects:
① After image scrambling, we will get a disordered image, which has no content, texture and shape, from which we can't read meaningful information.
When we embed such a "three noes" image into another ordinary image, it is not easy to cause too much change in the content, texture and shape of the image, or even detect the change. In this way, it is not easy for human eyes to recognize, so as to escape from the sight of a third party, so as to better ensure the concealment of watermark information
② Because the secret image is the image after scrambling, it is difficult for the third party to make statistical analysis on its content, texture and shape. In this way, even if they intercept the secret image, they can't do anything about it. If the third party attempts to perform anti scrambling operation on the secret image, it is also very difficult, because there are many methods of image scrambling. Each method can use different scrambling algorithms and set different parameters. The encrypting party can get many different results according to its own ideas, which brings great difficulties to the third party attempting to perform anti scrambling, It takes a huge amount of computation to exhaustively test various possibilities.
③ If the anti scrambling operation of the third party fails, it may also be maliciously modified on the hidden carrier. The purpose of resisting these attacks can also be achieved by scrambling. Because when the legal receiver anti scrambles the secret image, the information painted by the third party on the image will be scattered to all positions of the picture, forming dot random noise, which has little impact on vision.

Fig. 1 is a secret image restored after two malicious modifications: erasure and clipping on the scrambled image. It can be seen that the content of the secret image is still visible. In order to make the extracted image information clearer, the severely damaged image can also be processed by median filtering to remove random noise.
Of course, it should not be ignored that image scrambling increases the complexity and amount of encryption calculation to a certain extent, but compared with the larger amount of calculation that illegal attackers may spend, image scrambling is still a relatively safe means worth paying a price. Because of this, image scrambling technology plays a very important role and significance in digital watermarking technology.

2 digital image scrambling method
Digital image scrambling can be carried out in position space, color space and frequency space. With the development of computer technology and digital image processing technology, many literatures put forward different scrambling algorithms for image scrambling, which can be divided into linear transformation, geometric transformation and affine transformation. At present, many scrambling technologies are studied, including Fibonacci transform, Arnold transform, Hilbert curve transform, E-curve transform, Gray transform, affine transform, magic square, orthogonal Latin square transform and so on. No matter which scrambling technology is reversible or periodic, that is, multiple iterations or inverse transformation can restore the original image.
Next, only Arnold transform is taken as an example to discuss digital image scrambling.

2.1 Arnold transform
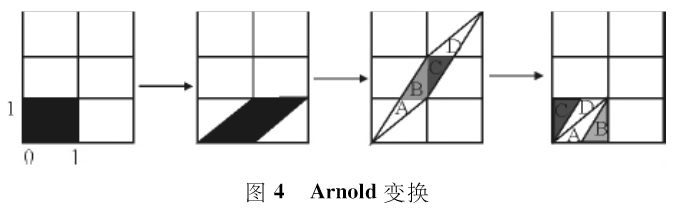
Arnold transformation is a transformation proposed by V.J. Arnold in the study of ergodic theory. It originally means catmapping, commonly known as cat face transformation. Arnold transform is intuitive, simple, periodic and easy to use. The principle of Arnold transformation is to make the staggered transformation in the x-axis direction first, and then the staggered transformation in the y-axis direction. The final modular operation is equivalent to the cutting and backfilling operation. The transformation diagram is shown in Figure 4.

The scrambling effect of Arnold transform is shown in Figure 5.



3 evaluation of image scrambling effect

Generally, the evaluation of image scrambling degree should mainly consider the following aspects: ① the moving distance of pixels; ② Uniformity of pixel dispersion; ③ The difference from the original image; ④ Image visual perception effect.
Generally speaking, the more "chaotic" the scrambled secret image is, the better its concealment and security are. From the concept of scrambling transformation, it can be seen that the essence of position space scrambling is to move the positions of each pixel of the original image. Intuitively, the greater the distance the pixel moves, the greater the degree of scrambling. On the other hand, after the pixel position is moved, the uniformity of pixel dispersion should also be considered. If the local pixels of the image move parallel in the same direction, the scrambling effect is not ideal even if the translation distance is large.
Generally speaking, the more evenly the original pixels are scattered after scrambling, the better the scrambling effect of the image. Moreover, the purpose of scrambling transformation is to hide the information of the original image to the greatest extent. Therefore, the greater the difference between the scrambled image and the original image, the better the scrambling effect is. Although the scrambling transformation does not change the gray value of the pixels of the original image, it will change the gray value distribution in the neighborhood of the pixels, so the more "scrambled" the scrambled image is relative to the original image, It shows that the more effective the scrambling algorithm is.

2, Source code

function varargout = ladingfang(varargin)
% LADINGFANG M-file for ladingfang.fig
%      LADINGFANG, by itself, creates a new LADINGFANG or raises the existing
%      singleton*.
%
%      H = LADINGFANG returns the handle to a new LADINGFANG or the handle to
%      the existing singleton*.
%
%      LADINGFANG('CALLBACK',hObject,eventData,handles,...) calls the local
%      function named CALLBACK in LADINGFANG.M with the given input arguments.
%
%      LADINGFANG('Property','Value',...) creates a new LADINGFANG or raises the
%      existing singleton*.  Starting from the left, property value pairs are
%      applied to the GUI before ladingfang_OpeningFunction gets called.  An
%      unrecognized property name or invalid value makes property application
%      stop.  All inputs are passed to ladingfang_OpeningFcn via varargin.
%
%      *See GUI Options on GUIDE's Tools menu.  Choose "GUI allows only one
%      instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help ladingfang

% Last Modified by GUIDE v2.5 05-Jan-2005 22:18:40

% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',       mfilename, ...
                   'gui_Singleton',  gui_Singleton, ...
                   'gui_OpeningFcn', @ladingfang_OpeningFcn, ...
                   'gui_OutputFcn',  @ladingfang_OutputFcn, ...
                   'gui_LayoutFcn',  [] , ...
                   'gui_Callback',   []);
if nargin & isstr(varargin{1})
    gui_State.gui_Callback = str2func(varargin{1});
end

if nargout
    [varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
    gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT

% --- Executes just before ladingfang is made visible.
function ladingfang_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
% varargin   command line arguments to ladingfang (see VARARGIN)

% Choose default command line output for ladingfang
handles.output = hObject;

% Update handles structure
guidata(hObject, handles);

% This sets up the initial plot - only do when we are invisible
% so window can get raised using ladingfang.
if strcmp(get(hObject,'Visible'),'off')
%   plot(rand(5));
end
global h1 h2
h1=handles.axes1;
h2=handles.axes2;
%-----------------Initialize interface properties
set(handles.edit1,'string','1');
set(handles.edit2,'string','2');
set(handles.edit3,'string','125');
set(handles.pushbutton2,'Visible','off');
G=imread('LENA256.BMP');
set(gcf,'CurrentAxes',h1);
imshow(G);
title('Original image');
set(h2,'Visible','off');

% UIWAIT makes ladingfang wait for user response (see UIRESUME)
% uiwait(handles.figure1);


% --- Outputs from this function are returned to the command line.
function varargout = ladingfang_OutputFcn(hObject, eventdata, handles)
% varargout  cell array for returning output args (see VARARGOUT);
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout{1} = handles.output;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%  Encryption function %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
axes(handles.axes1);
cla;

global h1 h2
%------------Update and obtain the properties of each object
Times = str2num(get(handles.edit1, 'string'));
X= str2num(get(handles.edit2, 'string'));
Y= str2num(get(handles.edit3, 'string'));
popup_sel_index = get(handles.popupmenu1, 'Value');
switch popup_sel_index
    case 1
        G=imread('lena256.bmp');
        set(gcf,'CurrentAxes',h1);
        imshow(G);
        title('Original image');
   %-----Verify the validity of input data
   N = str2double(get(handles.edit1,'String'));
   Errstr = '';
   if isnan(N) | ~(floor(N) == N) | (N <= 0)
      Errstr = 'The number of transformations must be a positive integer!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   D(1) =str2double(get(handles.edit2,'String'));
   D(2) =str2double(get(handles.edit3,'String'));
   Errstr = '';
   if isnan(D(1)) | ~(floor(D(1)) == D(1)) | (D(1) < 1)| (D(1)>255)
      Errstr = 'Parameter 1 must be a positive integer from 1 to 255!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   Errstr = '';
   if isnan(D(2)) | ~(floor(D(2)) == D(2)) | (D(2) < 1)| (D(1)>255)
      Errstr = 'Parameter 2 must be a positive integer from 1 to 255!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   
   if D(1) == D(2)
      Errstr = 'Parameter 1 and parameter 2 must be different!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
%-----------End of verification   
        %-----------Some controls are disabled during calculation
        mousefrm(0,'watch'); 
        set(handles.popupmenu1,'enable','off');
        set(handles.popupmenu2,'enable','off');
        set(handles.edit1,'enable','off');
        set(handles.edit2,'enable','off');
        set(handles.edit3,'enable','off');
        set(handles.pushbutton1,'enable','off');
        set(handles.pushbutton2,'enable','off');
        %----------------------------------------
        set(gcf,'CurrentAxes',h2);
        I=G;
        [u,v]=zhengjiaodui(X,Y);
        zhiluan(I,Times,u,v,1);
        title('After encryption');
        %----------Restore control availability
        set(handles.popupmenu1,'enable','on');
        set(handles.popupmenu2,'enable','on');
        set(handles.edit1,'enable','on');
        set(handles.edit2,'enable','on');
        set(handles.edit3,'enable','on');
        set(handles.pushbutton1,'enable','on');
        set(handles.pushbutton2,'enable','on');
        mousefrm(0,'arrow'); 
        %--------------------------------------
        
    case 2
        G=imread('LENA256.BMP');
        set(gcf,'CurrentAxes',h1);
        imshow(G);
        title('Original image');
        %-----Verify the validity of input data
   N = str2double(get(handles.edit1,'String'));
   Errstr = '';
   if isnan(N) | ~(floor(N) == N) | (N <= 0)
      Errstr = 'The number of transformations must be a positive integer!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   D(1) =str2double(get(handles.edit2,'String'));
   D(2) =str2double(get(handles.edit3,'String'));
   Errstr = '';
   if isnan(D(1)) | ~(floor(D(1)) == D(1))
      Errstr = 'Parameter 1 must be an integer!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   Errstr = '';
   if isnan(D(2)) | ~(floor(D(2)) == D(2)) 
      Errstr = 'Parameter 2 must be an integer!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
%-----------End of verification   
        mousefrm(0,'watch'); 
        set(gcf,'CurrentAxes',h2);
        positiontrans(G,Times,X,Y);
        title('After encryption');
        mousefrm(0,'arrow'); 
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%  Decryption function %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton2 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
axes(handles.axes1);
cla;
global  h1 h2 
Times = str2num(get(handles.edit1, 'string'));
X= str2num(get(handles.edit2, 'string'));
Y= str2num(get(handles.edit3, 'string'));
Times = str2num(get(handles.edit1, 'string'));
UNCODE=imread('code.bmp');
set(gcf,'CurrentAxes',h1);
imshow(UNCODE);
title('Before decryption');
%-----Verify the validity of input data
   N = str2double(get(handles.edit1,'String'));
   Errstr = '';
   if isnan(N) | ~(floor(N) == N) | (N <= 0)
      Errstr = 'The number of transformations must be a positive integer!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   D(1) =str2double(get(handles.edit2,'String'));
   D(2) =str2double(get(handles.edit3,'String'));
   Errstr = '';
   if isnan(D(1)) | ~(floor(D(1)) == D(1)) | (D(1) < 1)| (D(1)>255)
      Errstr = 'Parameter 1 must be a positive integer from 1 to 255!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   Errstr = '';
   if isnan(D(2)) | ~(floor(D(2)) == D(2)) | (D(2) < 1)| (D(1)>255)
      Errstr = 'Parameter 2 must be a positive integer from 1 to 255!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end
   
   if D(1) == D(2)
      Errstr = 'Parameter 1 and parameter 2 must be different!';
   end
   if ~isempty(Errstr)
      errordlg(Errstr);
      return
   end

3, Operation results

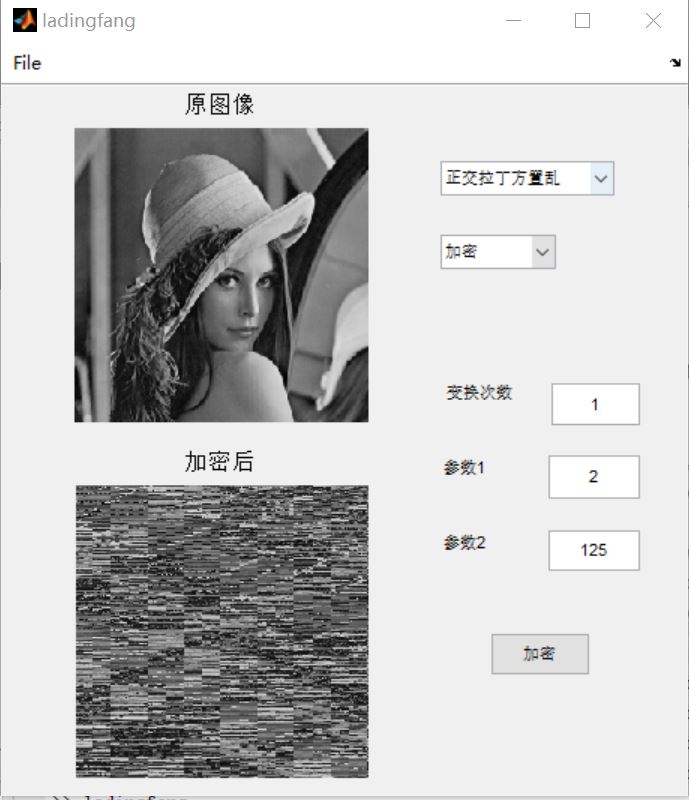
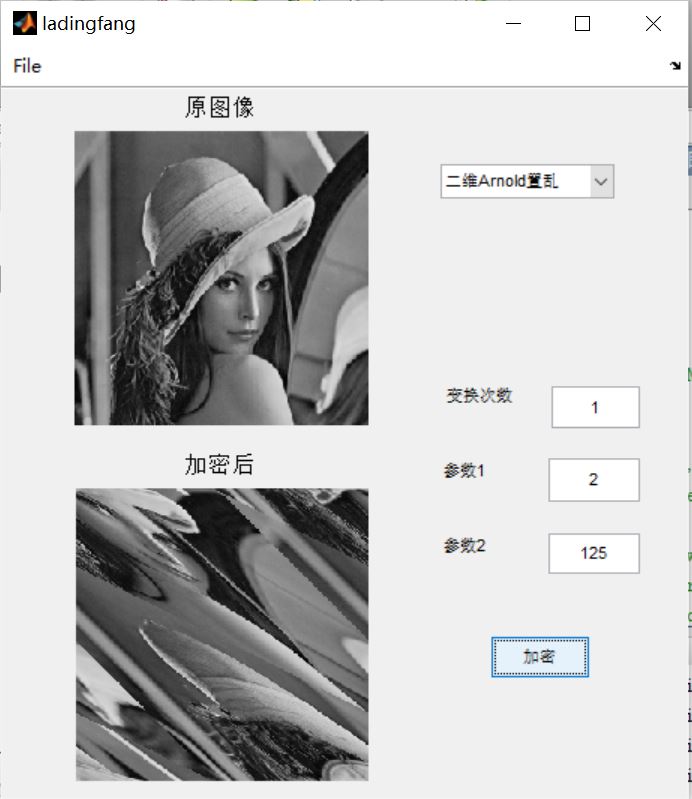
4, Remarks

Add or write complete QQ code