Reference link first
[motion control] Apollo 6 MPC of 0_ Controller parsing
For detailed derivation of vehicle lateral dynamics model, please refer to my other blog
Horizontal control principle and core code line by line analysis of Apollo control module
Because it is similar to the code and framework of LQR control in the above link, only the code is not repeated here, and the principle is mainly introduced
MPC transverse and longitudinal control principle



I mpc_controller framework
See Apollo / modules / control / controller / MPC for the code_ controller. cc
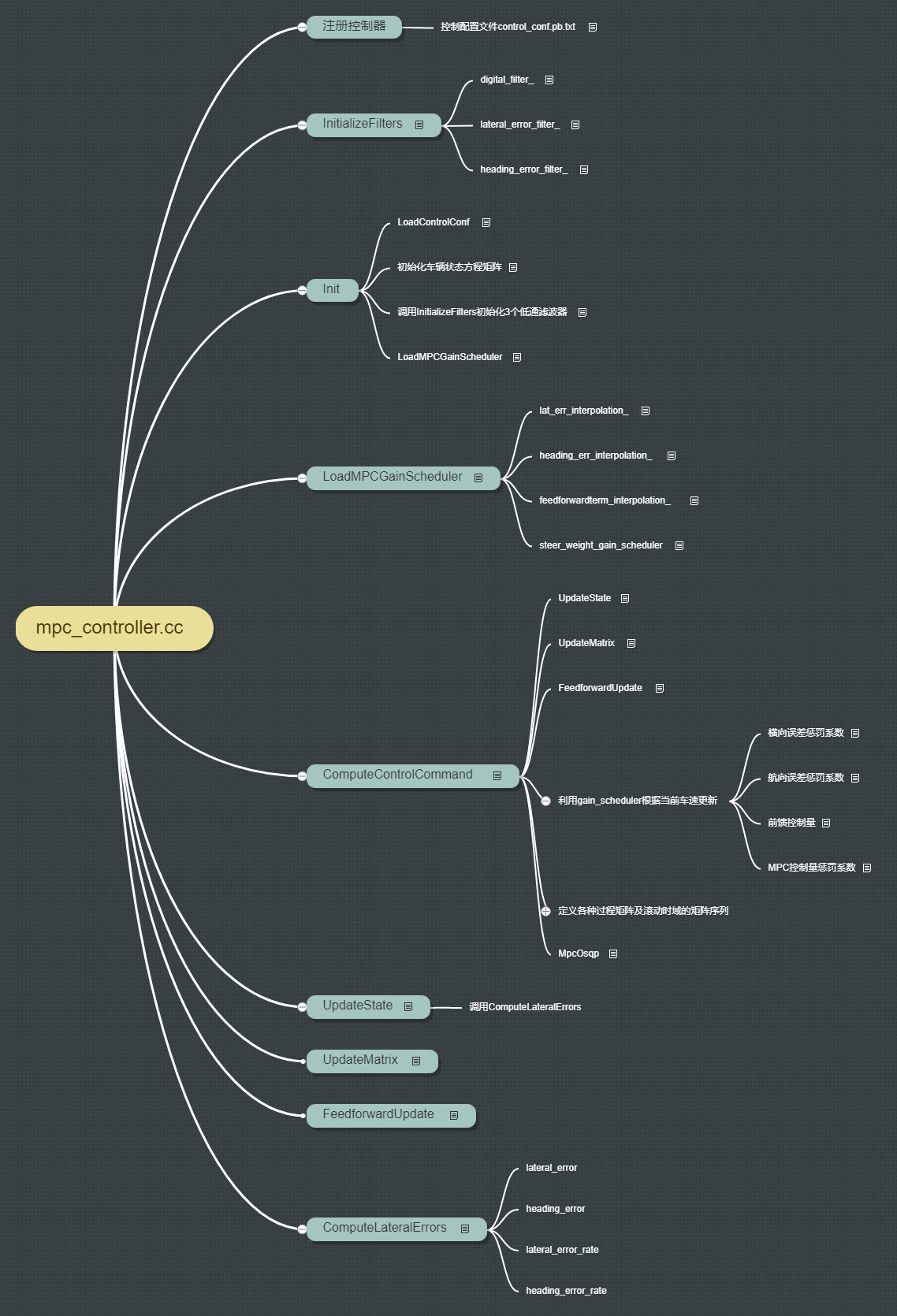
1.1 registered controller
\modules\control\conf\control_conf.pb.txt active_controllers: MPC_CONTROLLER
active_controllers: LON_CONTROLLER activates mpc horizontally and Loncontroller vertically
Activate different controllers here.
1.2 InitializeFilters
Initialize 3 lpf low-pass filters
digital_filter_: The second-order digital filter is used to filter the steering wheel angle control command
lateral_error_filter_: The mean low-pass filter filters the transverse error CTE, and the size of the filtering window is mean_filter_window_size in control_conf.pb.txt is defined as 10 cycles
heading_error_filter_: Mean low-pass filter to filter the heading error, and the filter window size is mean_filter_window_size is the same as lateral_error_filter_
1.3 Init
1.3.1 LoadControlConf
LoadControlConf: loads the parameters in the control configuration file into the data member of the MPCLatController class
1.3.2 # initialize vehicle state equation matrix
Vehicle lateral state equation
X'=AX+Bu+B1*(φdes)'
initialization
The constant term in matrix A, including the subsequent processing of velocity term;
B matrix, and x ts are discretized;
B1 is initialized to a 4x1 0 matrix;
The X-state matrix is initialized to a 4x1 0 matrix;
The Q matrix in MPC initializes the 4x4 matrix and reads it from the configuration file;
The R matrix in MPC is initialized to 1x1 unit matrix and read from the configuration file;
1.3.3 # call InitializeFilters to initialize three low-pass filters
1.3.4 LoadMPCGainScheduler
Load gain schedule from control configuration
There are four gain schedules in total
lat_err_interpolation_: Load the gain table of the lateral error in the control configuration file to the MPCController data member along with the vehicle speed. The larger the vehicle speed, the smaller the weight coefficient of the lateral error in the Q matrix
heading_err_interpolation_: Load the heading error in the control configuration file to the MPCController data member along with the gain table of the vehicle speed. The larger the vehicle speed is, the smaller the weight coefficient of the heading error in the Q matrix. The low speed focuses on the lateral error and the high speed focuses on the heading error.
feedforwardterm_interpolation_: Gain table of feedforward term
steer_weight_gain_scheduler: the gain table of the control quantity. The penalty coefficient x of the control quantity in the R matrix is the ratio interpolated according to the vehicle speed. The higher the vehicle speed, the greater the penalty coefficient of the control quantity and the greater the ratio
1.4 ComputeControlCommand
UpdateState
Function function:
1. Calculate various error items required for horizontal control, and put the amount into the debug pointer;
2. Update vehicle status matrix_state_, Take out the lateral / heading error / error rate directly from the debug pointer in the previous step
UpdateMatrix
It mainly updates the terms related to speed in matrices A and B1 in the vehicle state equation
matrix_a_
matrix_c_
FeedforwardUpdate
steer_angle_feedforwardterm_
It mainly updates the feedforward term in the vehicle state equation, including the speed related term
Using gain_ The scheduler updates according to the current vehicle speed
Lateral error penalty coefficient, heading error penalty coefficient, feedforward control quantity, MPC control quantity penalty coefficient
Define various process matrices and matrix sequences in rolling time domain
Call MpcOsqp optimization solver
Enter various parameters and constraints and call \ modules\common\math\mpc_osqp.cc
Call the member function solve of MpcOsqp class, put the solution result into the control sequence, take out the control quantity at the first time and distribute it.
This control quantity is subject to speed limiting, filtering, percentage limiting and finally issued.
1.5 UpdateState
Function function:
1. Call ComputeLateralErrors to calculate various error items required for horizontal control, and put the amount into the debug pointer;
2. Update vehicle status matrix_state_, Take out the lateral / heading error / error rate directly from the debug pointer in the previous step
1.6 UpdateMatrix
It mainly updates the terms related to speed in matrices A and B1 in the vehicle state equation
matrix_a_
matrix_c_
1.7 FeedforwardUpdate
steer_angle_feedforwardterm_
It mainly updates the feedforward term in the vehicle state equation, including the speed related term
1.8 ComputeLateralErrors
Calculate the lateral error correlation and put it into the debug pointer
II mpc_osqp solver
OSQP quadratic programming optimization solver, which solves MPC problems. The code is located in Apollo / modules / common / math / MPC_ OSQP. In CC, MpcOsqp class is defined, which mainly realizes the function of OSQP to optimize and solve MPC problems.
2.1 framework
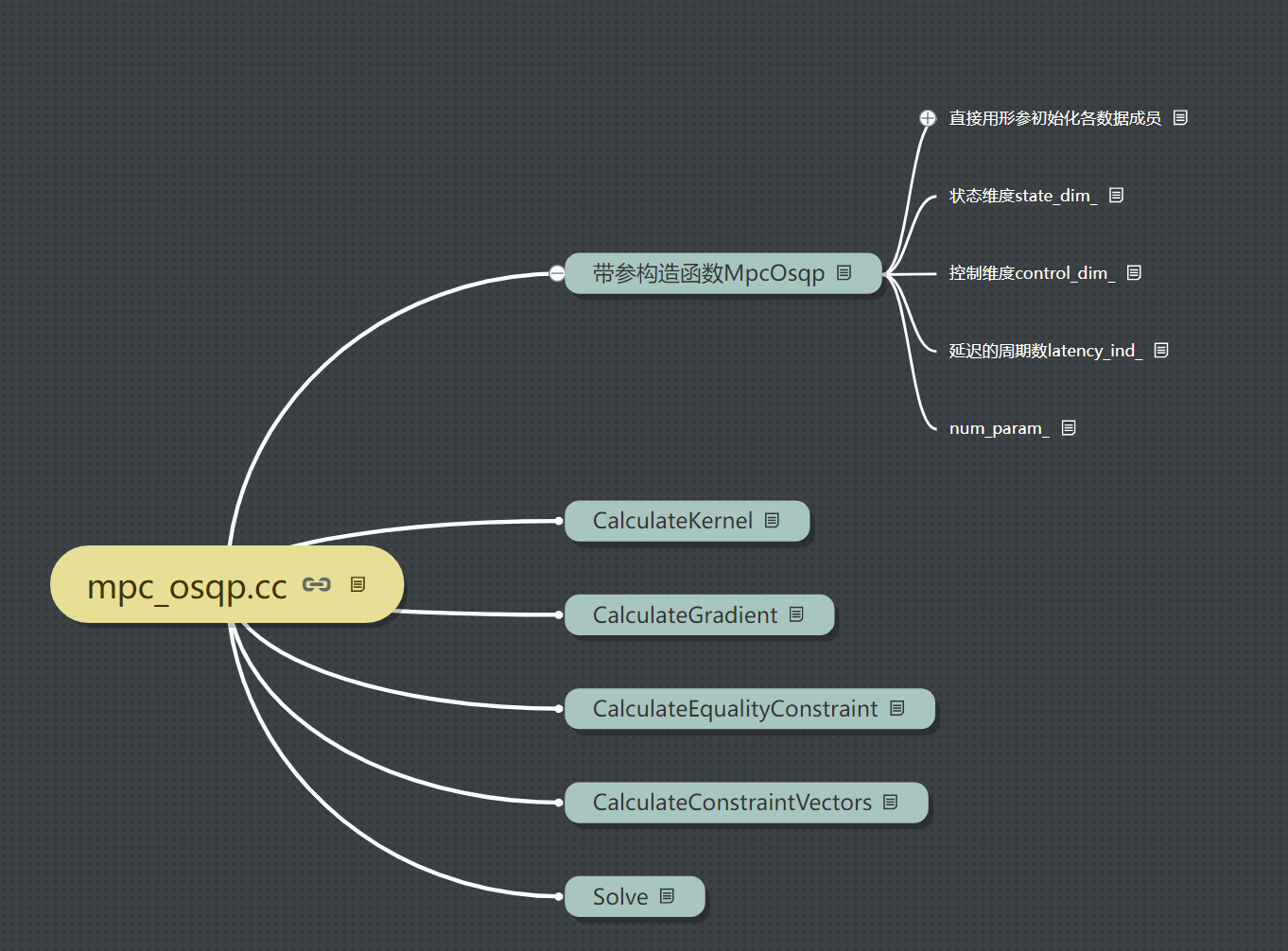
2.2 constructor with parameters MpcOsqp
Input matrix Ad,Bd,Q,R, initial state matrix X0, upper and lower boundaries of control quantity, upper and lower boundaries of state quantity, reference state (0 matrix), maximum number of iterations mpc_max_iteration_, Predict the number of cycles in time domain horizon_, Solution accuracy mpc_eps_
MpcOsqp::MpcOsqp(const Eigen::MatrixXd &matrix_a,
const Eigen::MatrixXd &matrix_b,
const Eigen::MatrixXd &matrix_q,
const Eigen::MatrixXd &matrix_r,
const Eigen::MatrixXd &matrix_initial_x,
const Eigen::MatrixXd &matrix_u_lower,
const Eigen::MatrixXd &matrix_u_upper,
const Eigen::MatrixXd &matrix_x_lower,
const Eigen::MatrixXd &matrix_x_upper,
const Eigen::MatrixXd &matrix_x_ref, const int max_iter,
const int horizon, const double eps_abs)
: matrix_a_(matrix_a),
matrix_b_(matrix_b),
matrix_q_(matrix_q),
matrix_r_(matrix_r),
matrix_initial_x_(matrix_initial_x),
matrix_u_lower_(matrix_u_lower),
matrix_u_upper_(matrix_u_upper),
matrix_x_lower_(matrix_x_lower),
matrix_x_upper_(matrix_x_upper),
matrix_x_ref_(matrix_x_ref),
max_iteration_(max_iter),
horizon_(horizon),
eps_abs_(eps_abs) {
state_dim_ = matrix_b.rows();
control_dim_ = matrix_b.cols();
ADEBUG << "state_dim" << state_dim_;
ADEBUG << "control_dim_" << control_dim_;
num_param_ = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_;
}state_dim_ Is the dimension of the state matrix, equal to the number of rows of matrix Bd
control_dim_ Is the dimension of the control matrix, equal to the number of columns of matrix Bd
num_param_ Is the number of parameters contained in the variable X to be solved by the OSQP solver
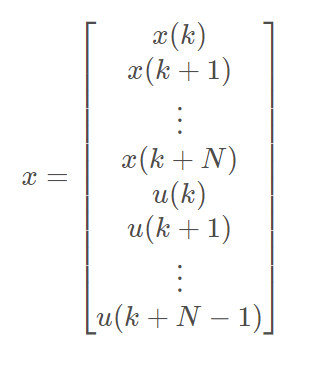
2.3 CalculateKernel
Calculating the matrix P in the standard form of quadratic programming
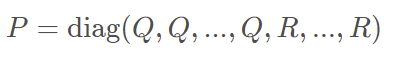
void MpcOsqp::CalculateKernel(std::vector<c_float> *P_data,
std::vector<c_int> *P_indices,
std::vector<c_int> *P_indptr) {
// col1:(row,val),...; col2:(row,val),....; ...
std::vector<std::vector<std::pair<c_int, c_float>>> columns;
columns.resize(num_param_);
size_t value_index = 0;
// state and terminal state
for (size_t i = 0; i <= horizon_; ++i) {
for (size_t j = 0; j < state_dim_; ++j) {
// (row, val)
columns[i * state_dim_ + j].emplace_back(i * state_dim_ + j,
matrix_q_(j, j));
++value_index;
}
}
// control
const size_t state_total_dim = state_dim_ * (horizon_ + 1);
for (size_t i = 0; i < horizon_; ++i) {
for (size_t j = 0; j < control_dim_; ++j) {
// (row, val)
columns[i * control_dim_ + j + state_total_dim].emplace_back(
state_total_dim + i * control_dim_ + j, matrix_r_(j, j));
++value_index;
}
}
CHECK_EQ(value_index, num_param_);
int ind_p = 0;
for (size_t i = 0; i < num_param_; ++i) {
// TODO(SHU) Check this
P_indptr->emplace_back(ind_p);
for (const auto &row_data_pair : columns[i]) {
P_data->emplace_back(row_data_pair.second); // val
P_indices->emplace_back(row_data_pair.first); // row
++ind_p;
}
}
P_indptr->emplace_back(ind_p);
}This function is not completely understood, but the first two for loops are well understood, that is, inserting Q and R matrices into Hessian matrix P of QP problem
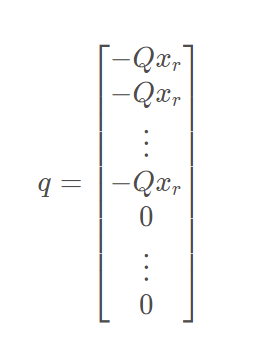
2.4 CalculateGradient
Calculating the matrix q in the standard form of quadratic programming
// reference is always zero
void MpcOsqp::CalculateGradient() {
// populate the gradient vector
gradient_ = Eigen::VectorXd::Zero(
state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
for (size_t i = 0; i < horizon_ + 1; i++) {
gradient_.block(i * state_dim_, 0, state_dim_, 1) =
-1.0 * matrix_q_ * matrix_x_ref_;
}
ADEBUG << "Gradient_mat";
ADEBUG << gradient_;
}But here, because the reference state matrix of Apollo input_ x_ Ref is always 0. In fact, q is always a 0 matrix
2.5 CalculateEqualityConstraint

Calculating matrix Ac in quadratic programming constraints

void MpcOsqp::CalculateEqualityConstraint(std::vector<c_float> *A_data,
std::vector<c_int> *A_indices,
std::vector<c_int> *A_indptr) {
static constexpr double kEpsilon = 1e-6;
// block matrix
Eigen::MatrixXd matrix_constraint = Eigen::MatrixXd::Zero(
state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) +
control_dim_ * horizon_,
state_dim_ * (horizon_ + 1) + control_dim_ * horizon_);
Eigen::MatrixXd state_identity_mat = Eigen::MatrixXd::Identity(
state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1));
ADEBUG << "state_identity_mat" << state_identity_mat;
matrix_constraint.block(0, 0, state_dim_ * (horizon_ + 1),
state_dim_ * (horizon_ + 1)) =
-1 * state_identity_mat;
ADEBUG << "matrix_constraint";
ADEBUG << matrix_constraint;
Eigen::MatrixXd control_identity_mat =
Eigen::MatrixXd::Identity(control_dim_, control_dim_);
for (size_t i = 0; i < horizon_; i++) {
matrix_constraint.block((i + 1) * state_dim_, i * state_dim_, state_dim_,
state_dim_) = matrix_a_;
}
ADEBUG << "matrix_constraint with A";
ADEBUG << matrix_constraint;
for (size_t i = 0; i < horizon_; i++) {
matrix_constraint.block((i + 1) * state_dim_,
i * control_dim_ + (horizon_ + 1) * state_dim_,
state_dim_, control_dim_) = matrix_b_;
}
ADEBUG << "matrix_constraint with B";
ADEBUG << matrix_constraint;
Eigen::MatrixXd all_identity_mat =
Eigen::MatrixXd::Identity(num_param_, num_param_);
matrix_constraint.block(state_dim_ * (horizon_ + 1), 0, num_param_,
num_param_) = all_identity_mat;
ADEBUG << "matrix_constraint with I";
ADEBUG << matrix_constraint;
std::vector<std::vector<std::pair<c_int, c_float>>> columns;
columns.resize(num_param_ + 1);
int value_index = 0;
// state and terminal state
for (size_t i = 0; i < num_param_; ++i) { // col
for (size_t j = 0; j < num_param_ + state_dim_ * (horizon_ + 1);
++j) // row
if (std::fabs(matrix_constraint(j, i)) > kEpsilon) {
// (row, val)
columns[i].emplace_back(j, matrix_constraint(j, i));
++value_index;
}
}
ADEBUG << "value_index";
ADEBUG << value_index;
int ind_A = 0;
for (size_t i = 0; i < num_param_; ++i) {
A_indptr->emplace_back(ind_A);
for (const auto &row_data_pair : columns[i]) {
A_data->emplace_back(row_data_pair.second); // value
A_indices->emplace_back(row_data_pair.first); // row
++ind_A;
}
}
A_indptr->emplace_back(ind_A);
}
Insert a, B and I into Ac according to the block matrix
Eigen library Eigen::MatrixXd defines matrix blocking operation functions Usage of block()

2.7 CalculateConstraintVectors
Calculate the upper and lower boundary matrices l,u in quadratic programming constraints
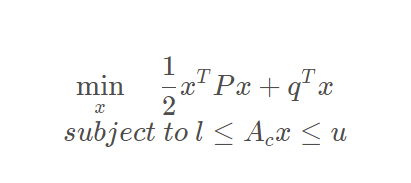

void MpcOsqp::CalculateConstraintVectors() {
// evaluate the lower and the upper inequality vectors
Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero(
state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero(
state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
for (size_t i = 0; i < horizon_; i++) {
lowerInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0,
control_dim_, 1) = matrix_u_lower_;
upperInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0,
control_dim_, 1) = matrix_u_upper_;
}
ADEBUG << " matrix_u_lower_";
for (size_t i = 0; i < horizon_ + 1; i++) {
lowerInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_lower_;
upperInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_upper_;
}
ADEBUG << " matrix_x_lower_";
// evaluate the lower and the upper equality vectors
Eigen::VectorXd lowerEquality =
Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1), 1);
Eigen::VectorXd upperEquality;
lowerEquality.block(0, 0, state_dim_, 1) = -1 * matrix_initial_x_;
upperEquality = lowerEquality;
lowerEquality = lowerEquality;
ADEBUG << " matrix_initial_x_";
// merge inequality and equality vectors
lowerBound_ = Eigen::MatrixXd::Zero(
2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
lowerBound_ << lowerEquality, lowerInequality;
ADEBUG << " lowerBound_ ";
upperBound_ = Eigen::MatrixXd::Zero(
2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
upperBound_ << upperEquality, upperInequality;
ADEBUG << " upperBound_";
}2.8 Solve
The quadratic programming is solved according to the input matrix. The solution result takes out the control sequence and puts it into cmd, and then the first control quantity in cmd can be used for control.
bool MpcOsqp::Solve(std::vector<double> *control_cmd)