Author: Nicholas C. Zakas
Translate: Crazy Technology House
Original: https://humanwhocodes.com/blo...
Reproduction is strictly prohibited without permission
One of the most commonly used and discussed data structures in computer science is Binary Search Tree .This is usually the first data structure introduced with a non-linear interpolation algorithm.A binary search tree is similar to a double-linked list, where each node contains some data and two pointers to other nodes; they differ in how they are related to each other.The pointer to a binary search tree node is often referred to as "left" and "right" to indicate the subtree associated with the current value.The simple JavaScript implementation of this node is as follows:
var node = { value: 125, left: null, right: null };
As you can see from the name, the binary search tree is organized into a hierarchical tree structure.The first item becomes the root node, and each additional value is added to the tree as an ancestor of the root.However, the values on the nodes of the binary search tree are unique and are sorted according to the values they contain: the value as the left subtree of the node is always smaller than the value of the node, and the value in the right subtree is always larger than the value of the node.In this way, finding values in a binary search tree becomes very simple, moving to the left as long as the value you are looking for is less than the node being processed and to the right if it is larger.You cannot have duplicates in a binary search tree because duplication breaks the relationship.The following diagram represents a simple binary search tree.
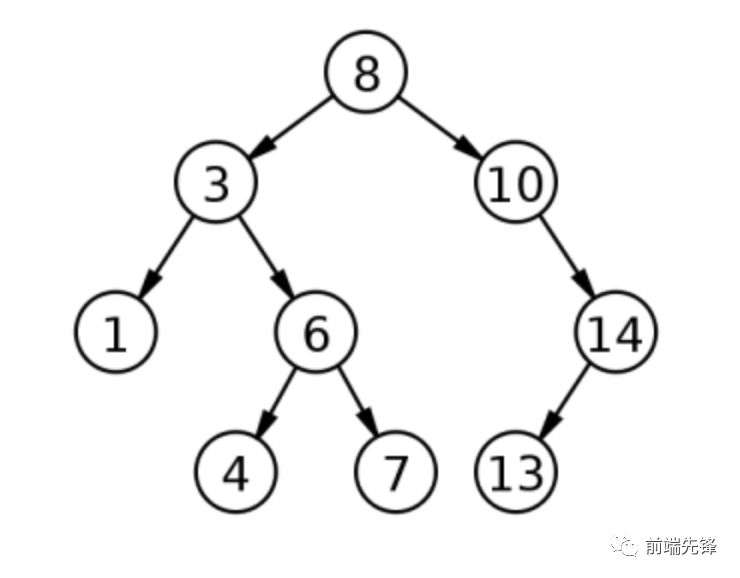
The figure above represents a binary search tree with a root value of 8.When a value of 3 is added, it becomes the left child node of the root because 3 is less than 8.When a value of 1 is added, it becomes the left child node of 3 because 1 is less than 8 (so left) and 1 is less than 3 (then left).When a value of 10 is added, it becomes the right child node to follow, because 10 is greater than 8.Continue processing values 6, 4, 7, 14, and 13 with this process.The depth of this binary search tree is 3, meaning that the node farthest from the root is three nodes.
Binary search trees end in a naturally ordered order, so they can be used to quickly find data because you can eliminate the possibility of each step immediately.By limiting the number of nodes you need to find, you can search faster.Suppose you want to find the value 6 in the tree above.Starting at the root, determine that 6 is less than 8, so go to the left child node of the root.Since 6 is greater than 3, you will go to the right node.You will find the right value.So you only need to visit three nodes instead of nine to find this value.
To implement a binary search tree in JavaScript, the first step is to define the basic interface:
function BinarySearchTree() { this._root = null; } BinarySearchTree.prototype = { //restore constructor constructor: BinarySearchTree, add: function (value){ }, contains: function(value){ }, remove: function(value){ }, size: function(){ }, toArray: function(){ }, toString: function(){ } };
Basic join is similar to other data structures in that it has methods for adding and deleting values.I also added some convenient methods, size(), toArray(), and toString(), which are useful for JavaScript.
To master how to use a binary search tree, it is best to start with the contains () method.The contains() method takes a value as a parameter and returns true if the value exists in the tree, or false if it does not.This method follows a basic binary search algorithm to determine if the value exists:
BinarySearchTree.prototype = { //more code contains: function(value){ var found = false, current = this._root //make sure there's a node to search while(!found && current){ //if the value is less than the current node's, go left if (value < current.value){ current = current.left; //if the value is greater than the current node's, go right } else if (value > current.value){ current = current.right; //values are equal, found it! } else { found = true; } } //only proceed if the node was found return found; }, //more code };
The search starts at the root of the tree.If you don't add data, you may not have a root, so you must check it.Traversing the tree follows the simple algorithm discussed earlier: if the value to be found is less than the current node, it moves to the left, and if the value is greater, it moves to the right.The current pointer is overwritten each time until the value to be found (in this case foundis set to true) or there are no more nodes in that direction (in this case, the value is not in the tree).
The method used in contains() can also be used to insert new values into a tree.The main difference is that you want to find where to place the new value, not in the tree:
BinarySearchTree.prototype = { //more code add: function(value){ //create a new item object, place data in var node = { value: value, left: null, right: null }, //used to traverse the structure current; //special case: no items in the tree yet if (this._root === null){ this._root = node; } else { current = this._root; while(true){ //if the new value is less than this node's value, go left if (value < current.value){ //if there's no left, then the new node belongs there if (current.left === null){ current.left = node; break; } else { current = current.left; } //if the new value is greater than this node's value, go right } else if (value > current.value){ //if there's no right, then the new node belongs there if (current.right === null){ current.right = node; break; } else { current = current.right; } //if the new value is equal to the current one, just ignore } else { break; } } } }, //more code };
When adding values to a binary search tree, the special case is when there is no root.In this case, simply set the root to a new value to do the work easily.For other cases, the basic algorithm is identical to the one used in contains(): the new value is less than the current node to the left, and if the value is larger, it is to the right.The main difference is that when you can't move on, this is where the new value is.So if you need to move left without a left node, the new value will become the left node (the same as the right node).Since there are no duplicates, if a node with the same value is found, the operation will stop.
Before moving on to the size() method, I want to go into tree traversal.To calculate the size of a binary search tree, each node in the tree must be accessed.Binary search trees usually have different types of traversal methods, most commonly ordered traversal.Ordered traversal is performed on each node by processing the left subtree, then the node itself, then the right subtree.Since the binary search tree is sorted this way, from left to right, the result is that the nodes are processed in the correct sort order.For the size() method, the order in which nodes are traversed is not really important, but it is important for the toArray() method.Since both methods require traversal, I decided to add a traverse() method that can be used generically:
BinarySearchTree.prototype = { //more code traverse: function(process){ //helper function function inOrder(node){ if (node){ //traverse the left subtree if (node.left !== null){ inOrder(node.left); } //call the process method on this node process.call(this, node); //traverse the right subtree if (node.right !== null){ inOrder(node.right); } } } //start with the root inOrder(this._root); }, //more code };
This method accepts a parameter process, which is a function that should run on each node in the tree.This method defines an auxiliary function called inOrder() to recursively traverse the tree.Note that if the current node exists, recursion moves only left and right (to avoid processing null s multiple times).The traverse() method then traverses sequentially from the root node, and the process() function processes each node.You can then use this method to implement size(), toArray(), and toString():
BinarySearchTree.prototype = { //more code size: function(){ var length = 0; this.traverse(function(node){ length++; }); return length; }, toArray: function(){ var result = []; this.traverse(function(node){ result.push(node.value); }); return result; }, toString: function(){ return this.toArray().toString(); }, //more code };
Both size() and toArray () call the traverse() method and pass in a function to run on each node.With size(), the function simply increments the length variable, while toArray () uses the function to add the value of the node to the array.The toString() method converts the returned array to a string and returns it before calling toArray().
When deleting a node, you need to determine if it is the root node.Root nodes are handled similarly to other nodes, with the obvious exception that the root node needs to be set to a different value at the end.For simplicity, this will be considered a special case of JavaScript code.
The first step in deleting a node is to determine if it exists:
BinarySearchTree.prototype = { //more code here remove: function(value){ var found = false, parent = null, current = this._root, childCount, replacement, replacementParent; //make sure there's a node to search while(!found && current){ //if the value is less than the current node's, go left if (value < current.value){ parent = current; current = current.left; //if the value is greater than the current node's, go right } else if (value > current.value){ parent = current; current = current.right; //values are equal, found it! } else { found = true; } } //only proceed if the node was found if (found){ //continue } }, //more code here };
The first part of the remove() method uses a binary search to locate the node to be deleted, moving left if the value is less than the current node, and right if the value is greater than the current node.Parent nodes are also tracked as you traverse because you eventually need to delete the node from its parent node.When found is equal to true, the current value is the node to be deleted.
There are three conditions to note when deleting a node:
- Leaf Node
- Node with only one child
- Node with two children
Deleting content other than leaf nodes from a binary search tree means that values must be moved to properly sort the tree.The first two are relatively simple to implement, deleting only one leaf node, deleting a node with one child node and replacing it with its child nodes.The last scenario is a bit complex for later access.
Before you know how to delete a node, you need to know exactly how many child nodes exist on the node.Once you know this, you must determine if the node is the root node, leaving a fairly simple decision tree:
BinarySearchTree.prototype = { //more code here remove: function(value){ var found = false, parent = null, current = this._root, childCount, replacement, replacementParent; //find the node (removed for space) //only proceed if the node was found if (found){ //figure out how many children childCount = (current.left !== null ? 1 : 0) + (current.right !== null ? 1 : 0); //special case: the value is at the root if (current === this._root){ switch(childCount){ //no children, just erase the root case 0: this._root = null; break; //one child, use one as the root case 1: this._root = (current.right === null ? current.left : current.right); break; //two children, little work to do case 2: //TODO //no default } //non-root values } else { switch (childCount){ //no children, just remove it from the parent case 0: //if the current value is less than its //parent's, null out the left pointer if (current.value < parent.value){ parent.left = null; //if the current value is greater than its //parent's, null out the right pointer } else { parent.right = null; } break; //one child, just reassign to parent case 1: //if the current value is less than its //parent's, reset the left pointer if (current.value < parent.value){ parent.left = (current.left === null ? current.right : current.left); //if the current value is greater than its //parent's, reset the right pointer } else { parent.right = (current.left === null ? current.right : current.left); } break; //two children, a bit more complicated case 2: //TODO //no default } } } }, //more code here };
When working with the root node, this is a simple process to override it.For non-root nodes, the corresponding pointer on the parent must be set based on the value of the node to be deleted: if the deleted value is less than the parent node, the left pointer must be reset to null (for nodes without children) or the left pointer of the deleted node; if the deleted value is greater than the parent, the right pointer must be resetA right pointer to a null or deleted node.
As mentioned earlier, deleting a node with two children is the most complex operation.Consider the following representation of a binary search tree.

Root is 8, left is 3, what happens if 3 is deleted?There are two possibilities: 1 (the left child, called the ordered predecessor) or 4 (the leftmost child of the right subtree, called the ordered successor) can replace 3.
Either of these options is appropriate.To find an ordered precursor, which is the value before the value is deleted, check the left subtree of the node to be deleted and select the rightmost child node; find the ordered successor, the value that appears immediately after the value is deleted, reverse the process, and check the leftmost right subtree.Each of these requires another tree traversal to complete the operation:
BinarySearchTree.prototype = { //more code here remove: function(value){ var found = false, parent = null, current = this._root, childCount, replacement, replacementParent; //find the node (removed for space) //only proceed if the node was found if (found){ //figure out how many children childCount = (current.left !== null ? 1 : 0) + (current.right !== null ? 1 : 0); //special case: the value is at the root if (current === this._root){ switch(childCount){ //other cases removed to save space //two children, little work to do case 2: //new root will be the old root's left child //...maybe replacement = this._root.left; //find the right-most leaf node to be //the real new root while (replacement.right !== null){ replacementParent = replacement; replacement = replacement.right; } //it's not the first node on the left if (replacementParent !== null){ //remove the new root from it's //previous position replacementParent.right = replacement.left; //give the new root all of the old //root's children replacement.right = this._root.right; replacement.left = this._root.left; } else { //just assign the children replacement.right = this._root.right; } //officially assign new root this._root = replacement; //no default } //non-root values } else { switch (childCount){ //other cases removed to save space //two children, a bit more complicated case 2: //reset pointers for new traversal replacement = current.left; replacementParent = current; //find the right-most node while(replacement.right !== null){ replacementParent = replacement; replacement = replacement.right; } replacementParent.right = replacement.left; //assign children to the replacement replacement.right = current.right; replacement.left = current.left; //place the replacement in the right spot if (current.value < parent.value){ parent.left = replacement; } else { parent.right = replacement; } //no default } } } }, //more code here };
The code for the root and non-root nodes with two children is almost the same.This implementation always finds ordered precursors by looking at the left subtree and finding the rightmost child node.Traversal is done using the replacement and replacementParent variables in the while loop.The node in the replacement eventually becomes the node that replaces the current, so it is removed from its current location by setting its parent's right pointer to the replaced left pointer.For the root node, when replacement is a direct child of the root node, the replacementParent will be null, so the right pointer of the replacement is only set to the right pointer of the root.The final step is to assign the replacement node to the correct location.For root nodes, the replacement is set to the new root; for non-root nodes, the replacement is assigned to the appropriate location on the original parent.
Instructions for this implementation: Always replacing nodes with ordered precursors may result in an unbalanced tree, with most of the values on one side of the tree.Unbalanced trees mean inefficient searches and should be of concern in real-world scenarios.In a binary search tree implementation, it is determined whether an ordered precursor or an ordered successor is used to maintain an appropriate balance of the tree (commonly referred to as a self-balanced binary search tree).
The complete source code for this binary search tree implementation can be found in my In GitHub Find it.For alternative implementations, you can also view Isaac Schlueter Of GitHub fork.
WeChat Public Number for the First Issue of this Article: A Pioneer
Welcome to Scan QR Code for Public Numbers and push you fresh front-end technical articles every day
Welcome to continue reading other great articles in this column:
- Deep understanding of Shadow DOM v1
- Step-by-step instructions for using WebVR to implement virtual reality games
- 13 modern CSS frameworks to help you develop more efficiently
- Quick Start BootstrapVue
- How does the JavaScript engine work?Everything you need to know from the call stack to Promise
- WebSocket Reality: Real-time communication between Node and React
- 20 interview questions about Git
- Deep parsing of Node.js console.log
- What on earth is Node.js?
- Build an API server with Node.js in 30 minutes
- Object Copy of Javascript
- Programmers earning less than 30K a month before age 30, where to go
- 14 Best JavaScript Data Visualization Libraries
- Eight top-level VS Code extensions to the front end
- Node.js multi-threaded full guide
- Four schemes and implementation of converting HTML to PDF
