1. Introduction

1 PCA
1.1 Data Dimension Reduction
The methods of dimension reduction include principal component analysis (PCA), factor analysis (FA), and independent component analysis (ICA).
Principal Component Analysis: Find a vector to minimize the sum of projections from each sample to that vector.
Factor analysis:
Independent component analysis:

1.2 PCA: The purpose is to reduce the dimension. The principle of dimension reduction is to maximize the objective function (maximum variance after data projection).
Push Principle Blog: https://blog.csdn.net/fendegao/article/details/80208723
(1) Suppose there are m n-dimensional samples: {Z1,Z2,..., Zm}
(2) The center u of the sample is: the sum of all the observed values of the sample /(mxn)
(3) After de-centralization, the matrix {X1,X2,..., Xm}={Z1-U,Z2-U,..., Zm-U} is obtained.
(4) When a vector W containing n elements is recorded, the projection of sample X1 in the w direction is the inner product of the two. W
(5) The objective function of PCA is to maximize the projection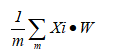

The objective equation can be solved as a matrix by:
(1) Lagrange operator is constructed, derivation is 0, and the vector with the largest projection is the eigenvector corresponding to the largest eigenvalue.
Based on the cumulative contribution ratio of the eigenvalues, you can specify how many W vectors to select as the K-L transformation matrix. If four principal components are selected, then for each n-dimensional sample, after the matrix transformation, it becomes (1x n)x(nx4)=1x4 dimension vector, which achieves the purpose of dimension reduction.
(2) SVD Singular Value Decomposition: To reduce dimensionality, only the right singular matrix, the eigenvector of AA(T), is obtained, and the covariance matrix of A is not required. Memory friendly.

1.3 Face Recognition Based on PCA
(1) Build a face database based on face sample database, such as real-world face photography (bank, station) and other data collection methods.
(2) Obtain the eigenvalues and eigenvectors of the covariance matrix of the training face database.
(3) For faces that need to be discriminated, determine which training sample has the closest projection on the eigenvector.

!!! Note: It is important to note that the covariance matrix is the covariance between dimensions, so it is nxn dimension, but in practical applications, such as image dimension reduction (assuming an image has 200*10 pixels and 100 images), one pixel is a dimension, then the original covariance matrix XX'is (2000x100) x (100x2000) dimension, computer storage calculation is too expensive, Consider using the substitution matrix P=X'X(100x2000)x(2000x100) instead: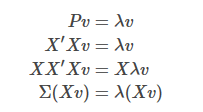

The eigenvalue of P is the eigenvalue of the original covariance matrix, and the eigenvector of P, left-multiplied by the data matrix, is the eigenvector of the original covariance matrix.

2 LDA
LDA: Linear Discriminant Analysis, also known as Fisher Linear Discriminant, is a commonly used dimension reduction technique.
The basic idea is that the high-dimensional pattern samples are projected into the optimal discriminant vector space to extract the classification information and compress the dimension of the feature space. After projection, the pattern samples are guaranteed to have the largest class-to-class distance and the smallest intra-class distance in the new subspace, that is, the pattern has the best separability in that space.
The dimension after LDA dimension reduction is directly related to the number of classes and has nothing to do with the dimension of the data itself. For example, the original data is n-dimensional and has a total of C classes, then after LDA dimension reduction, Dimension ranges from (1, C-1). For example, if image classification, two categories of positive and negative examples, each image is represented by a 10000-dimensional feature, then after LDA, there will be only one-dimensional feature, and this one-dimensional feature has the best classification ability.
For many of the two classifications, there is only one dimension left after LDA, so finding the best threshold seems OK.
Assuming that x is an N-dimensional column vector, to reduce x to C through LDA, you only need to find a projection matrix w, that is, an N*C matrix, which multiplies the transformation matrix of W by X and becomes C-dimensional. (The mathematical representation of a projection is to multiply by a matrix)
At this point, the key to the problem is to find a projection matrix! Furthermore, the projection matrix ensures that the pattern samples have the largest class-to-class distance and the smallest intraclass distance in the new subspace.

2.2 LDA mathematical representation:

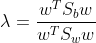
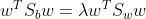
Source Code

clear all

clc

close all

start=clock;

sample_class=1:40;%Sample Category

sample_classnum=size(sample_class,2);%Number of sample categories

fprintf('Program Run Start....................\n\n');


for train_samplesize=3:8;

train=1:train_samplesize;%Each type of training sample

test=train_samplesize+1:10;%Each type of test sample


train_num=size(train,2);%Number of training samples per class

test_num=size(test,2);%Number of test samples per class


address=[pwd '\ORL\s'];

%Reading training samples

allsamples=readsample(address,sample_class,train);


%Use first PCA Dimension reduction

[newsample base]=pca(allsamples,0.9);

%Calculation Sw,Sb

[sw sb]=computswb(newsample,sample_classnum,train_num);


%Read Test Samples

testsample=readsample(address,sample_class,test);

best_acc=0;%Optimal Recognition Rate

%Finding the Optimal Projection Dimension

for temp_dimension=1:1:length(sw)

vsort1=projectto(sw,sb,temp_dimension);


%Projection of training samples and test samples, respectively

tstsample=testsample*base*vsort1;

trainsample=newsample*vsort1;

%Calculate recognition rate

accuracy=computaccu(tstsample,test_num,trainsample,train_num);

if accuracy>best_acc

best_dimension=temp_dimension;%Save optimal projection dimensions

best_acc=accuracy;

end

end

%---------------------------------Output Display----------------------------------

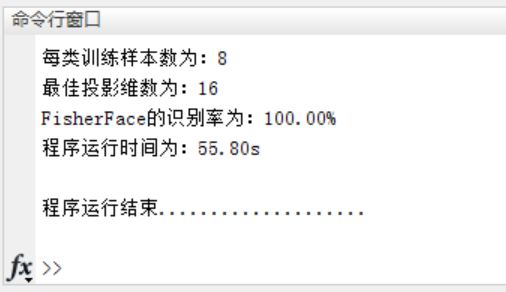
fprintf('The number of training samples per type is:%d\n',train_samplesize);

fprintf('The optimal projection dimension is:%d\n',best_dimension);

fprintf('FisherFace The recognition rate is:%.2f%%\n',best_acc*100);

fprintf('The program runs at:%3.2fs\n\n',etime(clock,start));

end

function [newsample basevector]=pca(patterns,num)

%The principal component analysis program, patterns Represents the input mode vector, num Is the control variable when num When greater than 1

%The required number of features is num，When num When 0 is greater than or equal to 1, the energy of the eigenvalue obtained is num

%Output: basevector Represents the eigenvector corresponding to the maximum eigenvalue obtained. newsample Represents in basevector

%Sample representation obtained under mapping.

[u v]=size(patterns);

totalsamplemean=mean(patterns);

for i=1:u

gensample(i,:)=patterns(i,:)-totalsamplemean;

end

sigma=gensample*gensample';

[U V]=eig(sigma);

d=diag(V);

[d1 index]=dsort(d);

if num>1

for i=1:num

vector(:,i)=U(:,index(i));

base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);

end

else

sumv=sum(d1);

for i=1:u

if sum(d1(1:i))/sumv>=num

l=i;

break;

end

end

for i=1:l

vector(:,i)=U(:,index(i));

base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);

end

end

function sample=readsample(address,classnum,num)

%This function is used to read samples.

%Input: address Is the address of the sample to be read,classnum Represents the category to be read into the sample,num Is a sample of each class;

%Output as Sample Matrix

allsamples=[];

image=imread([pwd '\ORL\s1_1.bmp']);%Read the first image

[rows cols]=size(image);%Number of rows and columns to get the image

for i=classnum

for j=num

a=imread(strcat(address,num2str(i),'_',num2str(j),'.bmp'));

b=a(1:rows*cols);

b=double(b);

allsamples=[allsamples;b];

end

end

3. Operation results