1, KD tree principle

   in this chapter, we will learn how to use KdTree to find K nearest neighbors of a specific point or location, and then we will also learn how to find all neighbors within a radius specified by the user (random in this example).

1) What is KD tree?

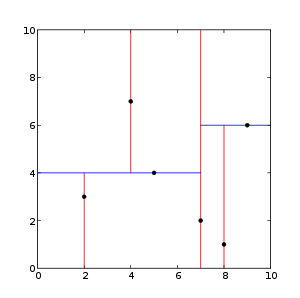
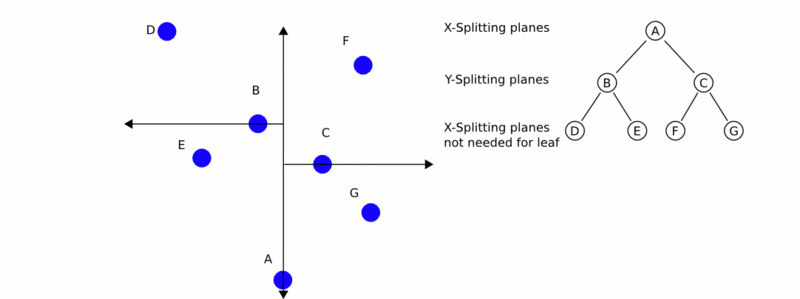
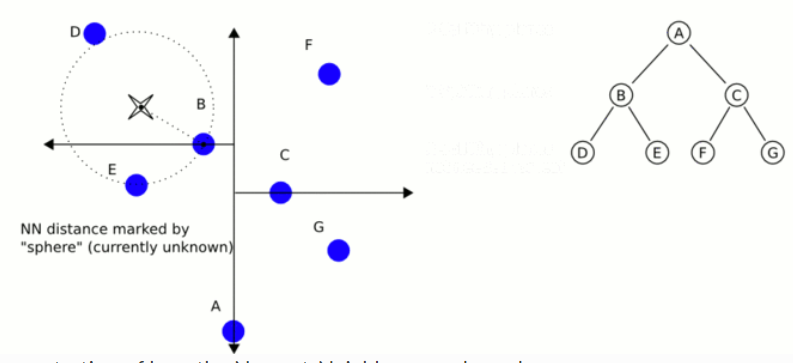
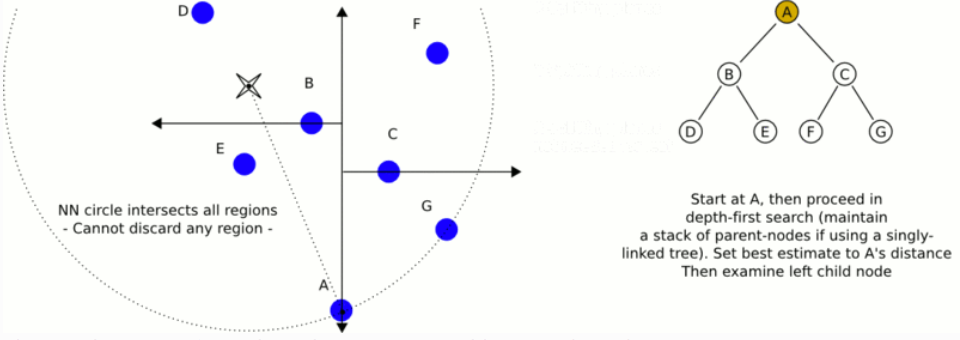
  k-dTree, called k-dimensional tree, is a data structure used to organize some points in k-dimensional space in computer science. It is a binary search tree. K-d tree is very useful for distance and nearest neighbor search. It is often used in feature point calculation or point cloud registration to reduce the search time. We usually only deal with three-dimensional point clouds, so all our k-d trees are three-dimensional. Each layer of k-d tree uses a hyperplane perpendicular to the corresponding axis to divide all child nodes along a specific dimension. At the root of the tree, all subtrees will be divided based on the first dimension (for example, if the coordinate of the first dimension is less than the root, it will be in the left subtree, and if it is greater than the root, it will be obviously in the right subtree). Each layer in the tree is divided down to the next dimension. When all other dimensions are exhausted, it returns to the first dimension. The most effective way to build a k-d tree is to use a sort division method. For example, in [quick sort], the median is placed on the root, the smaller value of one-dimensional value is placed on the left, and the larger value is placed on the right. Then repeat this process on the left and right subtrees until the last tree to be divided consists of only one element. The KD tree structure is established on the two-dimensional data, as shown in the figure below.

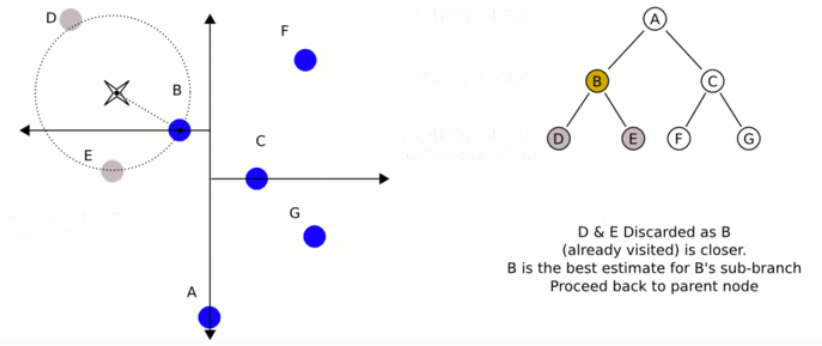
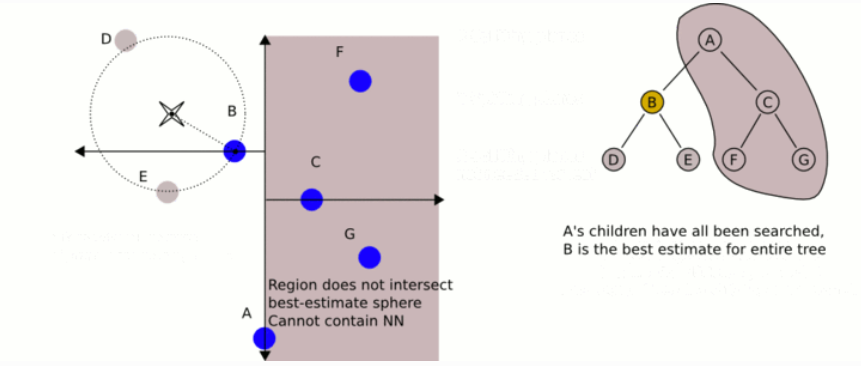
2) How to use PCL

   if you are not a student majoring in computational optimization, we only need to understand the principle of PCL, and we can tell why in the job interview. In practical use, we only need to know that the search speed can be accelerated by changing the point cloud into the arrangement of KD tree.
   how to use the KD tree structure, or how to arrange the point cloud in the form of KD tree, please see the following code:

#include <pcl/point_cloud.h>
#include <pcl/kdtree/kdtree_flann.h>

#include <iostream>
#include <vector>
#include <ctime>

int
main ()
{
  srand (time (NULL)); // Random seed 
// [1] Create point cloud pointer
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
// [2] Generate 1000 unordered point cloud data
  // Generate pointcloud data
  cloud->width = 1000;
  cloud->height = 1;
  cloud->points.resize (cloud->width * cloud->height);

  for (std::size_t i = 0; i < cloud->size (); ++i)
  {
    (*cloud)[i].x = 1024.0f * rand () / (RAND_MAX + 1.0f);
    (*cloud)[i].y = 1024.0f * rand () / (RAND_MAX + 1.0f);
    (*cloud)[i].z = 1024.0f * rand () / (RAND_MAX + 1.0f);
  }

// [3] Create KD tre object
  pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
// [4] Transfer data to KDTREE, that is, set the point cloud data to KDTREE structure
  kdtree.setInputCloud (cloud);
// [5] Randomly generate a point
  pcl::PointXYZ searchPoint;

  searchPoint.x = 1024.0f * rand () / (RAND_MAX + 1.0f);
  searchPoint.y = 1024.0f * rand () / (RAND_MAX + 1.0f);
  searchPoint.z = 1024.0f * rand () / (RAND_MAX + 1.0f);

  
  int K = 10;
 // [6]K nearest neighbor search, that is, search 10 points around the point
  std::vector<int> pointIdxKNNSearch(K);
  // [7] Set the search distance to 10
  std::vector<float> pointKNNSquaredDistance(K);

  std::cout << "K nearest neighbor search at (" << searchPoint.x 
            << " " << searchPoint.y 
            << " " << searchPoint.z
            << ") with K=" << K << std::endl;
// Start K-nearest neighbor search
  if ( kdtree.nearestKSearch (searchPoint, K, pointIdxKNNSearch, pointKNNSquaredDistance) > 0 )
  {
    for (std::size_t i = 0; i < pointIdxKNNSearch.size (); ++i)
      std::cout << "    "  <<   (*cloud)[ pointIdxKNNSearch[i] ].x 
                << " " << (*cloud)[ pointIdxKNNSearch[i] ].y 
                << " " << (*cloud)[ pointIdxKNNSearch[i] ].z 
                << " (squared distance: " << pointKNNSquaredDistance[i] << ")" << std::endl;
  }

  // Neighbors within radius search
// Search using radius search criteria
  std::vector<int> pointIdxRadiusSearch;
  std::vector<float> pointRadiusSquaredDistance;
// Randomly generate a search radius
  float radius = 256.0f * rand () / (RAND_MAX + 1.0f);
  std::cout << "Neighbors within radius search at (" << searchPoint.x 
            << " " << searchPoint.y 
            << " " << searchPoint.z
            << ") with radius=" << radius << std::endl;

// Start radius search
  if ( kdtree.radiusSearch (searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0 )
  {
    for (std::size_t i = 0; i < pointIdxRadiusSearch.size (); ++i)
      std::cout << "    "  <<   (*cloud)[ pointIdxRadiusSearch[i] ].x 
                << " " << (*cloud)[ pointIdxRadiusSearch[i] ].y 
                << " " << (*cloud)[ pointIdxRadiusSearch[i] ].z 
                << " (squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
  }


  return 0;
}