Chapter 3 - Mathematics, coordinates, cameras and component models

In Chapter 2, we have preliminarily discussed shaders. In this chapter, we will explore how to make objects move (most importantly, rotate) in OpenGL. It is assumed that you are already familiar with basic linear algebraic calculations: vector number multiplication, point multiplication and cross multiplication, matrix multiplication, etc.

Transformation matrix

Points in space [ p x , p y , p z , 1 ] T [p_x, p_y, p_z, 1]^T [px, py, pz, 1]T (homogeneous coordinates) undergoes some transformation E 4 × 4 E_{4 \times 4} E4 × After 4 ， the coordinates will change to E ⋅ [ p x , p y , p z , 1 ] T E \cdot [p_x, p_y, p_z, 1]^T E⋅[px​,py​,pz​,1]T； According to the types of transformations applied, they can be divided into translation, scaling and rotation.

In three-dimensional graphics, we often use the homogeneous coordinate form of point coordinates because we can't write if we don't use homogeneous coordinates E E The E matrix causes it to apply a translation transformation to the coordinates.

For a certain point in space, the fourth dimension of its coordinates is 1 1 1. For vectors such as "direction and axis" in space, the fourth dimension of their coordinates is 0 0 0.

• Scaling transforms are the simplest: scale along the three axes of space [ S x , S y , S z ] T [S_x, S_y, S_z]^T [Sx, Sy, Sz] T scale, and its transformation matrix is:

  E z o o m = [ S x 0 0 0 0 S y 0 0 0 0 S z 0 0 0 0 1 ] E_{zoom} = {\begin{bmatrix}{{S_x}}&0&0&0\\0&{{S_y}}&0&0\\0&0&{{S_z}}&0\\0&0&0&1\end{bmatrix}} Ezoom​=⎣⎢⎢⎡​Sx​000​0Sy​00​00Sz​0​0001​⎦⎥⎥⎤​

• Translation transformation: when the displacement is a vector in space [ d x , d y , d z ] T [d_x, d_y, d_z]^T When [dx, dy, dz] T, its transformation matrix is:

  E t r a n s = [ 1 0 0 d x 0 1 0 d y 0 0 1 d z 0 0 0 1 ] E_{trans} = {{\begin{bmatrix}1&0&0&{{d_x}}\\0&1&0&{{d_y}}\\0&0&1&{{d_z}}\\0&0&0&1\end{bmatrix}}} Etrans​=⎣⎢⎢⎡​1000​0100​0010​dx​dy​dz​1​⎦⎥⎥⎤​

• Rotation transformation: when around an axis in space [ A x , A y , A z ] T [A_x, A_y, A_z]^T [Ax, Ay, Az] T rotation angle θ \theta θ The transformation matrix is:

  E r o t a t e = [ cos ⁡ θ + A x 2 ( 1 − cos ⁡ θ ) A x A y ( 1 − cos ⁡ θ ) − A z sin ⁡ θ A x A z ( 1 − cos ⁡ θ ) + A y sin ⁡ θ 0 A x A y ( 1 − cos ⁡ θ ) + A z sin ⁡ θ cos ⁡ θ + A y 2 ( 1 − cos ⁡ θ ) A y A z ( 1 − cos ⁡ θ ) − A x sin ⁡ θ 0 A x A z ( 1 − cos ⁡ θ ) − A y sin ⁡ θ A y A z ( 1 − cos ⁡ θ ) + A x sin ⁡ θ cos ⁡ θ + A z 2 ( 1 − cos ⁡ θ ) 0 0 0 0 1 ] E_{rotate} = {\begin{bmatrix}{\cos \theta + {A_x}^2\left( {1 - \cos \theta } \right)}&{{A_x}{A_y}\left( {1 - \cos \theta } \right) - {A_z}\sin \theta }&{{A_x}{A_z}\left( {1 - \cos \theta } \right) + {A_y}\sin \theta }&0\\{{A_x}{A_y}\left( {1 - \cos \theta } \right) + {A_z}\sin \theta }&{\cos \theta + {A_y}^2\left( {1 - \cos \theta } \right)}&{{A_y}{A_z}\left( {1 - \cos \theta } \right) - {A_x}\sin \theta }&0\\{{A_x}{A_z}\left( {1 - \cos \theta } \right) - {A_y}\sin \theta }&{{A_y}{A_z}\left( {1 - \cos \theta } \right) + {A_x}\sin \theta }&{\cos \theta + {A_z}^2\left( {1 - \cos \theta } \right)}&0\\0&0&0&1\end{bmatrix}} Erotate​=⎣⎢⎢⎡​cosθ+Ax​2(1−cosθ)Ax​Ay​(1−cosθ)+Az​sinθAx​Az​(1−cosθ)−Ay​sinθ0​Ax​Ay​(1−cosθ)−Az​sinθcosθ+Ay​2(1−cosθ)Ay​Az​(1−cosθ)+Ax​sinθ0​Ax​Az​(1−cosθ)+Ay​sinθAy​Az​(1−cosθ)−Ax​sinθcosθ+Az​2(1−cosθ)0​0001​⎦⎥⎥⎤​

The compound transformation of multiple transformations is the matrix product of each molecular transformation. It should be noted here that since there is no exchange law in matrix multiplication, the exchange of the order of applying transformation will produce different transformation results. In most cases, it should be scaled first, then rotated, and finally flattened, so as to produce intuitive transformation results; Since the coordinate vector is multiplied on the right side of the matrix, in the composite matrix, the subsequent transformation should be multiplied on the left side of the previous matrix:

E = E t r a n s ⋅ E r o t a t e ⋅ E z o o m E = E_{trans} \cdot E_{rotate} \cdot E_{zoom} E=Etrans​⋅Erotate​⋅Ezoom​

Eigen math library

introduce

Eigen It is a matrix operation library written in pure generics, which was first developed by the open source organization KDE. It can be used as long as the header file is introduced. Its performance has reached the first-class level in a number of indicators and tests Intel MKL and CUDA As the back-end of high-performance computing, it is the computing library selected by many famous projects, such as TensorFlow, Large Hadron Collider and Krita. The license is MPL2. Download Eigen 3 and put the Eigen folder in the header file search path of the compiler.

The matrix types of Eigen are all from the template class Eigen:: matrix < T, rows, cols, option, max_ rows, max_ Cols >, vectors are special matrices (especially column vectors). To easily use matrix or vector types, just define generic type aliases:

template <GLuint Stage, typename T = float>
using Mat = Eigen::Matrix<T, Stage, Stage>;

template <GLuint Dim, typename T = float>
using Vec = Eigen::Matrix<T, Dim, 1>;

Implementation transformation matrix

We use Eigen to realize the function of "specifying parameters to obtain transformation matrix":

Mat<4> ZoomMatrix(const Vec<3>& scale) {
    return Mat<4> {
        { scale(0), 0.0f, 0.0f, 0.0f },
        { 0.0f, scale(1), 0.0f, 0.0f },
        { 0.0f, 0.0f, scale(2), 0.0f },
        { 0.0f, 0.0f, 0.0f, 1.0f },
    };
}

Mat<4> TransMatrix(const Vec<3>& displace) {
    return Mat<4> {
        { 1.0f, 0.0f, 0.0f, displace(0) },
        { 0.0f, 1.0f, 0.0f, displace(1) },
        { 0.0f, 0.0f, 1.0f, displace(2) },
        { 0.0f, 0.0f, 0.0f, 1.0f },
    };
}

Mat<4> RotateMatrix(float theta_rad, const Vec<3>& axis) {
    Vec<3> norm = axis.normalized().eval();

    // First calculate and save some repeatedly used results to avoid repeated calculation
    const float
        sinv = sin(theta_rad),
        cosv = cos(theta_rad),
        cosm = 1.0f - cosv,
        x2 = norm(0) * norm(0),
        y2 = norm(1) * norm(1),
        z2 = norm(2) * norm(2),
        xy = norm(0) * norm(1),
        yz = norm(1) * norm(2),
        xz = norm(0) * norm(2);

    return Mat<4> {
        { (cosv + x2 * cosm), (xy * cosm - norm(2) * sinv), (xz * cosm + norm(1) * sinv), 0.0f },
        { (xy * cosm + norm(2) * sinv), (cosv + y2 * cosm), (yz * cosm - norm(0) * sinv), 0.0f },
        { (xz * cosm - norm(1) * sinv), (yz * cosm + norm(0) * sinv), (cosv + z2 * cosm), 0.0f },
        { 0.0f, 0.0f, 0.0f, 1.0f }
    };
}

The Eigen matrix can be simply moved left into std::ios:

    std::cout << mat << std::endl;

Try to generate a rotation matrix and print:

    std::cout << RotateMatrix(45, Vec<3>{ 1.0f, 1.0f, 0.0f }) << std::endl;

Transform class

The above example is just an example to get familiar with Eigen quickly. In fact, Eigen has provided various transformation classes or functions (Scalar is a type parameter, we can fill in GLfloat):

• Scaling(scale): scale to scale proportionally. Note that scale needs to be GLfloat
• Scaling(rx, ry, rz): scale to rx along the x axis, shrink to ry along the y axis, and shrink to rz along the z axis. The parameter needs to be GLfloat
• Scaling(vec3): scale along any axis, and the scale of the three axes is given by a three-dimensional eigenvector
• Angleaxis < scalar > (rad, axis_norm): axis around any axis_ Norm (three-dimensional Eigen vector, which must be normalized vector) rotation radian rad
• Translation < scalar, 3 > (dx, dy, dz): three-dimensional displacement, moving dx, dy and dz respectively in three dimensions
• Translation < scalar, 3 > (vec3): three-dimensional displacement. The displacement is given by a three-dimensional Eigen vector

Eigen internally encapsulates different transformations with different types. In order to obtain a unified transformation matrix, we need to construct the transformation as Affine3f type (internally implemented as 4 × 4 4 \times 4 four × 4 matrix):

    Eigen::Affine3f transform(Eigen::Scaling((GLfloat)s));          // Produces a transformation matrix scaled equally to s

Composite transformation is to multiply the transformation matrix (the transformation after multiplication is on the left). The following two forms can be used:

    transform *= Eigen::AngleAxis<GLfloat>(rad, axis);              // Vec<3> axis(0, 0, 1);  Z axis
    transform = Eigen::AngleAxis<GLfloat>(rad, axis) * transform;

You can also use the chained API of Affine3f:

    transform.scale(s);                                             // This API does not accept Eigen::Scaling!
    transform.translate(Eigen::Vector3f(dx, dy, dz));               // This API does not accept Eigen::Translation!
    transform.rotate(Eigen::AngleAxis<GLfloat>(rad, axis));         // This API accepts Eigen::AngleAxis!

Set Uniform for matrix type

We also need a way to send the transformation matrix we build to the Uniform quantity of the shader. First, you need to declare a Uniform of matn type in the shader. Here n is the order of the square matrix, which can only be 2, 3 or 4, and can only be float type:

uniform mat4 transform;

We use the glUniformMatrix API to set the matrix type Uniform. It has three suffixes available: 2fv, 3fv and 4fv, which respectively represent matrices of order 2 ~ 4. The formal parameter table is (location, count, transfer, * matrix):

1. We are already familiar with location
2. To set values for count matrices, we only pass one matrix at a time, so just fill in 1
3. The value of the parameter transfer is GL_FALSE or GL_TRUE； When GL_ When true, the incoming matrix will be transpose d first, which is used to deal with the case that the storage form of the matrix is "row primary order", while Eigen is stored in column primary order by default, so it is set to GL_FALSE
4. Finally, pass in the first address matrix of the matrix, and we can call the data() method of the Eigen matrix to obtain a pointer that can be directly used here.

Therefore, we write some templates to determine the API to be called during compilation through type parameters, and are compatible with Eigen:

template <typename T, size_t Dim>
struct _GLUniformStaticSetter {
    ...
    static void set(GLint location, const Eigen::Matrix<typename std::enable_if<(Dim < 5), T>::type, Dim, 1>& values) { }
};
template <typename T>
struct _GLUniformStaticSetter<T, 1> {
    ...
    static void set(GLint location, const Eigen::Matrix<T, 1, 1>& values) {
        _set_uniform_value(location, values[0]);
    }
};
template <typename T>
struct _GLUniformStaticSetter<T, 2> {
    ...
    static void set(GLint location, const Eigen::Matrix<T, 2, 1>& values) {
        _set_uniform_value(location, values[0], values[1]);
    }
};
template <typename T>
struct _GLUniformStaticSetter<T, 3> {
    ...
    static void set(GLint location, const Eigen::Matrix<T, 3, 1>& values) {
        _set_uniform_value(location, values[0], values[1], values[2]);
    }
};
template <typename T>
struct _GLUniformStaticSetter<T, 4> {
    ...
    static void set(GLint location, const Eigen::Matrix<T, 4, 1>& values) {
        _set_uniform_value(location, values[0], values[1], values[2], values[3]);
    }
};

template<std::size_t Stage>
void glUniformMatrix(GLint location, const GLfloat* matrix) {
    static_assert(Stage > 1 && Stage < 5, "::glUniformMatrix: unsupported matrix size");
}
template<>
void glUniformMatrix<2>(GLint location, const GLfloat* matrix) {
    glUniformMatrix2fv(location, 1, GL_FALSE, matrix);
}
template<>
void glUniformMatrix<3>(GLint location, const GLfloat* matrix) {
    glUniformMatrix3fv(location, 1, GL_FALSE, matrix);
}
template<>
void glUniformMatrix<4>(GLint location, const GLfloat* matrix) {
    glUniformMatrix4fv(location, 1, GL_FALSE, matrix);
}

We're at globj Too many OpenGL uniform setters are written in HPP! For ease of management, put this code in a separate file, gluniform HPP (since almost all the codes in it have appeared in the previous article, the content will not be given here), and then in globj Referenced in HPP:

#include "gluniform.hpp"

Then, we add several overloads for glshaderprogram:: uniforminterface:: setter, and accept Eigen's vector, Matrix and transformation Matrix as parameters respectively (note that the order of Matrix cannot be generalized here, but can only be overloaded one by one, and the problem can come from Eigen):

// File: globj.hpp

...

// In GLShaderProgramObject::UniformInterface::Setter:
    template <typename T, std::size_t Dim>
    void operator=(const Eigen::Vector<T, Dim>& values) const { // Setter for Eigen vectors
        if (_location < 0) return;
        _GLUniformStaticSetter<T, Dim>::set(_location, values);
    }
    void operator=(const Eigen::Matrix2f& matrix) const {
        if (_location < 0) return;
        glUniformMatrix<2>(_location, matrix.data());
    }
    void operator=(const Eigen::Matrix3f& matrix) const {
        if (_location < 0) return;
        glUniformMatrix<3>(_location, matrix.data());
    }
    void operator=(const Eigen::Matrix4f& matrix) const {
        if (_location < 0) return;
        glUniformMatrix<4>(_location, matrix.data());
    }
    void operator=(const Eigen::Affine3f& transform) const {
        if (_location < 0) return;
        glUniformMatrix<4>(_location, transform.data());
    }

Next, we add a composite transformation in Application::renderFrame():

// File: application.hpp

...

// In Application:
    virtual void renderFrame() {
        constexpr float RAD_PER_DEG = 3.14159265359f / 180.0f;

        ...

        // Set uniforms
        _spo->uniforms["mainTex"] = 0;
        _spo->uniforms["subTex"] = 1;

        GLfloat t = (GLfloat)glfwGetTime();
        _spo->uniforms["externColor"] = {vary(t - 2.0f), vary(t), vary(t + 2.0f), 1.0f};

        Eigen::Vector3f axis(0.f, 0.f, 1.f);
        Eigen::Affine3f transform(Eigen::Scaling(cos(t)));
        transform.translate(Eigen::Vector3f(sin(t), 0, 0));
        transform.rotate(Eigen::AngleAxisf(t * 45.0f * RAD_PER_DEG, axis));
        _spo->uniforms["transform"] = transform;

        ...
    }

In the V shader (we haven't touched it for a long time!) Medium:

// File: myshader.vert

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTex;

out vec2 vTex;

uniform mat4 transform;

void main()
{
    gl_Position = transform * vec4(aPos, 1.0);
    vTex = aTex;
}

Running this program, you will see a square that changes color while performing compound geometric transformation:

coordinate transformation

So far, we have directly sent the coordinates of vertices in clipping space to GPU, and then directly (or after simple transformation) write GL in V_ Position； In fact, the vertex coordinates of 3D objects need to undergo multi-step transformation to reach the clipping space:

1. Vertex coordinates are initially located in local space (or model space)
2. As 3D objects are placed in the scene, the position of each vertex is transformed from local space to world space by the model matrix
3. Based on a view angle (called camera), the points in the world coordinate system are transformed into the observation space by the observation matrix
4. Finally, the points in the observation space are transformed into the clipping space through a projection matrix, which is the "stereo effect" produced in this transformation.

The transformation relationship of several spaces is shown in the following figure:

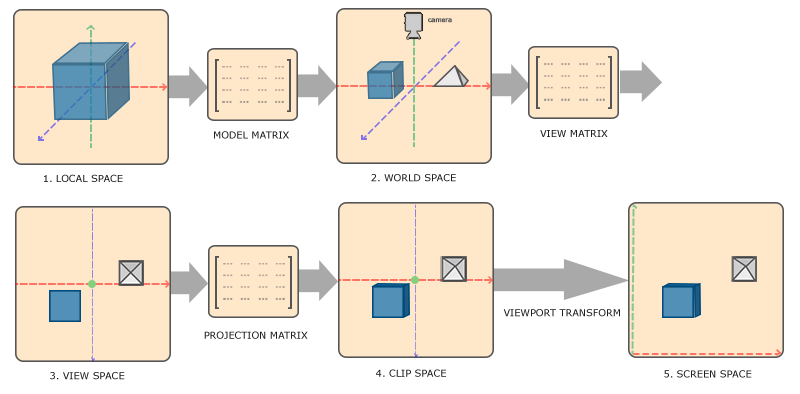
Local space

After the previous discussion, we come to the conclusion that the model is the coordinates of a series of vertices and the index of coordinates (used to indicate "which vertices form a triangular surface"), and generally includes one or several sets of texture coordinates of each vertex. In fact, the most basic 3D model file format stores this information.

In the original model data, the coordinate values of each vertex are calibrated relative to a model origin with a certain quantitative benchmark (for example, "how many coordinate units correspond to the actual 1cm"), and the space where the coordinate values of each vertex are located is the local space.

The origin of the model is generally located at the center of the model and the height is 0. For example, the humanoid model is "on the ground under your feet".

world space

In most cases, we need a space as the container of the model, that is, the "Scene", whose coordinate space is the world space. The coordinates of each vertex on the model reach the world space after a composite transformation in the same form as the above. This is the most understandable step of coordinate transformation. The matrix that completes this transformation is the model matrix (often referred to as M matrix).

Observation space and camera

Once the coordinates of model vertices in world space are determined, the scene is determined; The same scene can be viewed from countless perspectives, and what you see from each perspective is different. We use "camera" to refer to the observer of the scene. The coordinate space with the camera as the coordinate reference (origin) is the observation space (under the observation of the camera).

The camera must also have absolute coordinates in world space (otherwise we cannot determine where it is located) and a line of sight vector (in world space) to determine its angle of view. The coordinates and line of sight of the camera can be changed dynamically.

For a certain camera at any time, a certain observation matrix (often referred to as V matrix) can be obtained, so as to transform the coordinates in the world space into a new coordinate space with the camera as the reference (origin) and the line of sight direction as a coordinate axis (- Z axis), which is the observation space. The observation matrix is also a compound transformation in mathematical form.

OpenGL itself does not have the concept of camera. It is just a concept we imagined to simplify complex coordinate transformation. We will specifically discuss the calculation of observation matrix in the following paper; At present, we first use a simple displacement as the observation matrix:

    Eigen::Affine3f(Eigen::Translation3f(0.f, 0.f, -3.f))   // The simplest observation matrix is used to make up the number

Clipping space and viewport

As a specification, OpenGL requires all three dimensions of visible vertex coordinates to be located in [ − 1 , 1 ] [-1,1] Within [− 1,1], this coordinate space is the clipping space, and its name is very direct: after the rendering content of each frame is determined, OpenGL will eliminate all vertices beyond the coordinate value range of the clipping space to reduce the amount of calculation: triangles completely outside the clipping space are directly eliminated; For some triangles outside the clipping space, additional vertices will be "clipped"; Triangles completely within the clipping space are not processed. However, this coordinate regulation is inconvenient for most development situations. Therefore, the common practice is to transform the coordinates in the observation space into the clipping space through a transformation matrix, which is called projection matrix (often called P matrix). Its mathematical form is generally not compound transformation. For each different projection form, it has its own unique projection matrix.

The clipping space needs to undergo perspective division before it is transformed into screen space (that is, NDC).

Since we only care about the points that can enter the clipping range after the coordinates are projected, in the observation space, the coordinates that can enter the clipping space through transformation have a logical value range, which is called the viewing box. According to different projection forms, the viewing box may be a cube or a pyramid (or other geometric forms), Because they are generally columns or cones, they are collectively referred to as Visual body (viewing frustum, also known as viewing cone, because the viewing body of perspective projection is a pyramid).

Orthogonal projection

Orthogonal projection is a projection form, which does not conform to natural vision, but can well reflect the geometric shape, size and parallel edges of the object, that is, the equal scale projection commonly used in engineering, which may also be used in "2.5D style" games. The view of orthogonal projection is a box, as shown in the following figure:

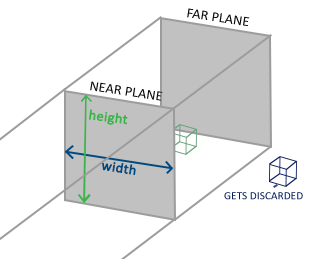
The visual body of orthogonal projection can be described by 6 parameters (note that the parameters are all values in the observation space):

1. Left plane coordinate x l x_l xl​
2. Right plane coordinate x r x_r xr​
3. Upper plane coordinates y t y_t yt​
4. Lower plane coordinates y b y_b yb​
5. Near plane distance z n z_n zn​
6. Far plane distance z f z_f zf​

Orthogonal projection matrix:

P o r t h o = [ 2 x r − x l 0 0 − x r + x l x r − x l 0 2 y t − y b 0 − y t + y b y t − y b 0 0 − 2 z f − z n − z f + z n z f − z n 0 0 0 1 ] P_{ortho} = {\begin{bmatrix}\frac{2}{x_r - x_l}&0&0&-\frac{x_r + x_l}{x_r - x_l}\\0&\frac{2}{y_t - y_b}&0&-\frac{y_t + y_b}{y_t - y_b}\\0&0&-\frac{2}{z_f - z_n}&-\frac{z_f + z_n}{z_f - z_n}\\0&0&0&1\end{bmatrix}} Portho​=⎣⎢⎢⎢⎡​xr​−xl​2​000​0yt​−yb​2​00​00−zf​−zn​2​0​−xr​−xl​xr​+xl​​−yt​−yb​yt​+yb​​−zf​−zn​zf​+zn​​1​⎦⎥⎥⎥⎤​

The implementation is as follows (MATH_EPS is the minimum quantity defined by us, take 1e-6):

Eigen::Matrix4f makeOrthographicProjection(const float l, const float r, const float t, const float d, const float z_near, const float z_far) {
    const float dx = r - l;
    const float dy = t - d;
    const float dz = z_far - z_near;
    if (dx < MATH_EPS) throw std::runtime_error("invalid left or right plane given");
    if (dy < MATH_EPS) throw std::runtime_error("invalid top or bottom plane given");
    if (dz < MATH_EPS) throw std::runtime_error("invalid z_near or z_far given");

    const float invx = 1.0f / dx;
    const float invy = 1.0f / dy;
    const float invz = -1.0f / dz;
    return Eigen::Matrix4f {
        {2.0f * invx, 0.0f, 0.0f, -(r + l) * invx},
        {0.0f, 2.0f * invy, 0.0f, -(t + d) * invy},
        {0.0f, 0.0f, 2.0f * invz, (z_far + z_near) * invz},
        {0.0f, 0.0f, 0.0f, 1.0f}
    };
}

perspective projection

Perspective projection is a projection in line with natural vision. Perspective projection is used in most 3D games. Its visual body is a pyramid, as shown in the following figure:

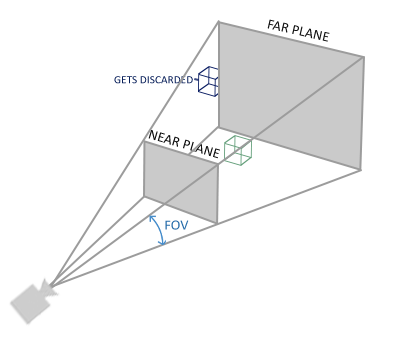
The visual body of perspective projection can be described by four parameters:

1. view ϕ \phi ϕ， It is the opening angle of the horizon (often referred to as FOV). The upper and lower line of sight angle of the human eye is about 45 degrees, so it is desirable in most cases ϕ = 4 5 ∘ \phi = 45^\circ ϕ=45∘
2. The aspect ratio is the quotient of the width and height of the projection plane a a a
3. Near plane distance z n z_n zn​
4. Far plane distance z f z_f zf​

Perspective projection matrix:

P p e r s p = [ 1 a ⋅ t a n ( ϕ 2 ) 0 0 0 0 1 t a n ( ϕ 2 ) 0 0 0 0 − z f + z n z f − z n − 2 z f z n z f − z n 0 0 − 1 0 ] P_{persp} = {\begin{bmatrix}\frac{1}{a \cdot tan({\frac{\phi}{2}})}&0&0&0\\0&\frac{1}{tan({\frac{\phi}{2}})}&0&0\\0&0&-\frac{z_f + z_n}{z_f - z_n}&-\frac{2 z_f z_n}{z_f - z_n}\\0&0&-1&0\end{bmatrix}} Ppersp​=⎣⎢⎢⎢⎡​a⋅tan(2ϕ​)1​000​0tan(2ϕ​)1​00​00−zf​−zn​zf​+zn​​−1​00−zf​−zn​2zf​zn​​0​⎦⎥⎥⎥⎤​

The implementation is as follows:

Eigen::Matrix4f makePerspectiveProjection(const float fov, const float aspect, const float z_near, const float z_far) {
    const float tanv = tan(0.5f * fov);
    const float dz = z_far - z_near;
    if (tanv < MATH_EPS && tanv > -MATH_EPS) throw std::runtime_error("invalid FOV given");
    if (aspect < MATH_EPS && aspect > -MATH_EPS) throw std::runtime_error("invalid aspect ratio given");
    if (dz < MATH_EPS) throw std::runtime_error("invalid z_near or z_far given");

    const float invz = -1.0f / dz;
    const float invtan = 1.0f / tanv;
    return Eigen::Matrix4f {
        {invtan / aspect, 0.0f, 0.0f, 0.0f},
        {0.0f, invtan, 0.0f, 0.0f},
        {0.0f, 0.0f, invz * (z_far + z_near), 2.0f * invz * z_far * z_near},
        {0.0f, 0.0f, -1.0f, 0.0f}
    };
}

Render a plane

Now that the three most important matrices M, V and P in the V shader have been introduced, we are about to take a key step from 2D to 3D: rendering a plane in 3D space. First, add a method getAspectRatio() to the Application class, which obtains the size of the current window from GLFW and returns the aspect ratio:

float getAspectRatio() const {
    int w, h;
    glfwGetWindowSize(_window, &w, &h);
    return (float)w / (float)h;
}

The following code is very concise. Just give the M, V and P matrices to the OpenGL API layer:

    // Set uniforms
    _spo->uniforms["mainTex"] = 0;
    _spo->uniforms["subTex"] = 1;

    _spo->uniforms["model"] = Eigen::Affine3f(Eigen::AngleAxisf(MATH_RAD_PER_DEG * -45.0f, Eigen::Vector3f(1.f, 0.f, 0.f)));
    _spo->uniforms["view"] = Eigen::Affine3f(Eigen::Translation3f(0.f, 0.f, -3.f));
    _spo->uniforms["projection"] = makePerspectiveProjection(MATH_RAD_PER_DEG * 45.f, getAspectRatio(), 0.1f, 100.f);

V shader:

// File: myshader.vert

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTex;

out vec2 vTex;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    vTex = aTex;
}

Running the program, we will see a plane with perspective shortening, and when we adjust the window size, it can always maintain the correct perspective proportion.

Deep cache

Let's try another cube. Model data:

GLModel<GLLayoutSingleUV> loadTexturedCube() {
    return {
        std::vector<GLLayoutSingleUV> {
            { { -0.5f, -0.5f, -0.5f }, { 0.0f, 0.0f } },
            { {  0.5f, -0.5f, -0.5f }, { 1.0f, 0.0f } },
            { {  0.5f,  0.5f, -0.5f }, { 1.0f, 1.0f } },
            { { -0.5f,  0.5f, -0.5f }, { 0.0f, 1.0f } },
            { { -0.5f, -0.5f,  0.5f }, { 0.0f, 0.0f } },
            { {  0.5f, -0.5f,  0.5f }, { 1.0f, 0.0f } },
            { {  0.5f,  0.5f,  0.5f }, { 1.0f, 1.0f } },
            { { -0.5f,  0.5f,  0.5f }, { 0.0f, 1.0f } },
            { { -0.5f,  0.5f,  0.5f }, { 1.0f, 0.0f } },
            { { -0.5f,  0.5f, -0.5f }, { 1.0f, 1.0f } },
            { { -0.5f, -0.5f, -0.5f }, { 0.0f, 1.0f } },
            { {  0.5f,  0.5f,  0.5f }, { 1.0f, 0.0f } },
            { {  0.5f, -0.5f, -0.5f }, { 0.0f, 1.0f } },
            { {  0.5f, -0.5f,  0.5f }, { 0.0f, 0.0f } },
            { {  0.5f, -0.5f, -0.5f }, { 1.0f, 1.0f } },
            { { -0.5f,  0.5f,  0.5f }, { 0.0f, 0.0f } }
        },

        std::vector<GLuint> {
            0, 1, 2, 2, 3, 0,
            4, 5, 6, 6, 7, 4,
            8, 9, 10, 10, 4, 8,
            11, 2, 12, 12, 13, 11,
            10, 14, 5, 5, 4, 10,
            3, 2, 11, 11, 15, 3
        }
    };
}

Use this model instead in the constructor of Application:

    // Load model
    auto model = loadTexturedCube();
    printf("Loaded model: %lld vertices, %lld indices\n", model.first.size(), model.second.size());

Don't forget that in the rendering cycle, this time we will render 36 vertices:

    // Draw call
    glDrawElements(GL_TRIANGLES, 36, GL_UNSIGNED_INT, nullptr);

Running the program, we get a "box" instead of a cube:

OpenGL does not know the order in which objects are drawn. The occlusion relationship between the front and back of objects is determined by the so-called depth test. The depth is a value (Z value) owned by each segment - remember the "mixing and testing" after F mentioned in Chapter 1? The depth test will test the Z value of all clips at the same pixel position, so as to discard the clips that should be occluded.

The depth test is turned off by default. You can turn it on with glEnable(feature):

    glEnable(GL_DEPTH_TEST);

After the depth test is enabled, the depth is like a new invisible channel in the image (it can also be understood as a layer). We need to clean it together when the screen is cleared every frame:

    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

Next, we rotate the cube and pass the amount of time to the shader (just change a section of the rendering cycle):

    // Set uniforms
    _spo->uniforms["mainTex"] = 0;
    _spo->uniforms["subTex"] = 1;

    GLfloat t = (GLfloat)glfwGetTime();
    _spo->uniforms["time"] = t * MATH_PI_HALF; // MATH_PI_HALF = 1.5707963...， That is, PI divided by 2

    Eigen::Affine3f m(Eigen::AngleAxisf(MATH_RAD_PER_DEG * 45.0f * t, Eigen::Vector3f(1.f, 1.f, 0.f).normalized()));
    Eigen::Affine3f v(Eigen::Translation3f(0.f, 0.f, -3.f));
    Eigen::Matrix4f p = makePerspectiveProjection(MATH_RAD_PER_DEG * 45.f, getAspectRatio(), 0.1f, 100.f);
    _spo->uniforms["model"] = m;
    _spo->uniforms["view"] = v;
    _spo->uniforms["projection"] = p;

Eigen:: angleaxis (angle, axis) requires that the incoming axis vector must be normalized, so we need to use normalized() method.

Make some changes in F:

// File: myshader.frag

#version 330 core
in vec2 vTex;

out vec4 FragColor;

uniform float time;
uniform sampler2D mainTex;
uniform sampler2D subTex;

void main()
{
    FragColor = mix(texture(mainTex, vTex), texture(subTex, vTex), 0.5 * sin(time) + 0.5);
}

Now we have a rotating cube, and the mixing ratio of the two maps changes over time:

Code abstraction

We have entered the 3D era. Now the urgent task is to systematically create the concept of "Scene" and abstract the "camera" class; By moving the camera, we can "walk" in the scene - although the feeling of the movement of the perspective is nothing more than the visual effect caused by a simple compound transformation, it looks so real.

Why is the composite transformation here "simple"? Because it contains only translation and rotation, not even (the most disgusting) scaling.

Look at the object

As mentioned earlier, a camera can be described using two vectors:

1. Camera position (point coordinates in world space)
2. Camera line of sight direction (vector in world space)

The position of the camera is needless to say; Generally speaking, we do not directly specify a line of sight direction for the camera, but associate it with a "watching object". The reason is very simple: when we look at things, we generally have a focus of attention, that is, watching the object. If the position of watching the object changes, the line of sight direction will change accordingly. If we directly specify the line of sight direction, it will bring unnecessary complexity; Otherwise, when the positions of the camera and the object are determined, it is very simple to obtain the line of sight direction, that is, the coordinate vector difference between the two points.

We can take any model (model origin) in the scene as the object watched by the camera; For "free camera", we also specify a virtual staring object "in front of the lens".

How to abstract the camera is obviously different from each other; Here's just my idea - you should realize your dream independently.

Transformer class

First, we abstract all coordinate transformations in world space as transformers, which are summarized as follows:

// File: transformer.hpp

class Transformer final {
private:
    Eigen::Vector3f _position { Eigen::Vector3f::Zero() };
    Eigen::Quaternionf _rotation { Eigen::Quaternionf::Identity() };
    Eigen::Vector3f _scale { Eigen::Vector3f::Ones() };
    Eigen::Affine3f _transform { Eigen::Affine3f::Identity() };

    void updateTransform() {
        _transform = Eigen::Affine3f { Eigen::Translation3f(_position) };
        _transform.rotate(_rotation).scale(_scale);
    }

public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    Transformer() = default;

    const Eigen::Vector3f& getPosition() const;
    const Eigen::Quaternionf& getRotation() const;
    const Eigen::Vector3f& getScale() const;
    const Eigen::Affine3f& getTransform() const;

    Transformer& resetTransform();
    Transformer& resetPosition();
    Transformer& resetRotation();
    Transformer& resetScale();

    Transformer& setPosition(const Transformer& transformer);
    Transformer& setPosition(float x, float y, float z);
    Transformer& setPosition(const Eigen::Vector3f& position);
    Transformer& setPosition(Eigen::Vector3f&& position);
    Transformer& addPosition(const Transformer& transformer);
    Transformer& addPosition(float x, float y, float z);
    Transformer& addPosition(const Eigen::Vector3f& position);

    Transformer& setRotation(const Transformer& transformer);
    Transformer& setRotation(float angle_deg, const Eigen::Vector3f& axis);
    Transformer& setRotation(const Eigen::AngleAxis<float>& rotation);
    Transformer& setRotation(const Eigen::Quaternionf& rotation);
    Transformer& setRotation(Eigen::Quaternionf&& rotation);
    Transformer& addRotation(const Transformer& transformer);
    Transformer& addRotation(float angle_deg, const Eigen::Vector3f& axis);
    Transformer& addRotation(const Eigen::AngleAxis<float>& rotation);
    Transformer& addRotation(const Eigen::Quaternionf& rotation);

    Transformer& setScale(const Transformer& transformer);
    Transformer& setScale(float scale_xyz);
    Transformer& setScale(float scale_x, float scale_y, float scale_z);
    Transformer& setScale(const Eigen::Vector3f& scale);
    Transformer& setScale(Eigen::Vector3f&& scale);
    Transformer& addScale(const Transformer& transformer);
    Transformer& addScale(float scale_xyz);
    Transformer& addScale(float scale_x, float scale_y, float scale_z);
    Transformer& addScale(const Eigen::Vector3f& scale);
};

Transformer simply saves position, rotation and scaling parameters and encapsulates Eigen's transformation API:

1. Save the current transformation parameters in the class, including position, rotation and scaling; Getters and setter s that provide these parameters
2. When the transformation parameters are changed through setter, the transformation matrix is updated; Otherwise, do not update
3. Save the transformation matrix (CACHE) after the transformation parameters were last updated in the class
4. The getter of the transformation matrix will directly return the cached constant reference without copy

Besides, here_ The quaternion class quaternion provided by Eigen is used for rotation, which is similar to the use method of AngleAxis type, but supports the superposition of rotation, so as to realize the necessary functions such as addRotation.

There is a strange problem here: it should be scaled, rotated and displaced first (SRT); However, in the actual test, the order needs to be reversed (TRS), and the transformation result is correct. The reason is unknown, which may be caused by the implementation of Eigen.

Our class contains a fixed size Eigen object as a member, so the macro Eigen provided by Eigen should be added to the public part_ MAKE_ ALIGNED_ OPERATOR_ New, so that Eigen can generate a memory aligned new operator for our class; If we don't add this macro, we have to manually define and disable the memory alignment of Eigen, otherwise it may cause runtime crash.

With Transformer, we can easily get the transformation matrix and improve the performance - now, when the parameters of a Transformer remain unchanged, we don't need to recalculate its transformation matrix.

Actor and Role

Component oriented development

With Transformer, we can (almost) forget about coordinate transformation because we have built a unified control API for it. Next, we are faced with a major design choice, namely "how to manage a large number of objects with different functions in the scene".

An effective abstract model is the so-called "component-based model", that is, in the scene, all program entities are "mounted" to an "object" with a specific location in the scene in the form of components. The object is responsible for managing all components mounted on it, executing various callbacks in the component life cycle, and when it is destroyed, Also destroy self mounted components.

1. We call the objects in the scene actors, namely "actors", and each Actor instance has a Transformer exclusively to save its own spatial position; It also maintains a component list, that is, the pointers of all components attached to itself;
2. We call the components that can be attached to the Actor Role, that is, "Role". An "Actor" can have multiple "roles" (or no roles at all). A derived class of Role can complete a specific function and behavior. For example, under this design idea, the concept of "Camera" refers to the Actor attached to the Role of Camera, As we can say, "this Actor plays the Role of Camera" - this sounds easy to understand and easy to write.

After introducing the concept of Role, our creativity has an outlet: by inheriting the Role class and mounting it on the Actor, we can realize various program functions that depend on spatial location; We can even say "all things are roles", which determines the component-oriented development mode: it is born out of object-oriented, but simplifies and avoids the complexity of traditional object-oriented, leaving a group of concise timing interfaces for complex secondary development.

In fact, most game engines have such a mechanism, which is enough to prove that Component-oriented development is effective in games and similar application scenarios - the word Role corresponds to MonoBehavior in Unity and Component in Unreal Engine!

Next, we have to decide how to manage all actors in the scene in a unified way. This is not an easy task, because there can be subordinate relationships between actors. For example, you may be eager for a character's weapons and clothes to always move with him (ha ha ha ha). Standing on the shoulders of giants, we know that we can use the tree data structure to manage the dependency relationship between actors: each Actor is the subtree of its parent Actor, and the root node of the whole tree is the center of our virtual scene; The root node is also a special Actor. It is a member of the management class Hierarchy of the scene, and other actors are saved in a table maintained by Hierarchy, so as to realize fast traversal and search.

The key to the problem is to choose one of the following design choices:

1. The node of the tree is the Actor object
2. The node of the tree is the shared node pointing to the Actor object_ PTR pointer

In case you don't know, shared_ptr is a smart pointer provided by the standard library from C++11. It has a "reference count" to record the current number of shared_ptr points to the same address. When the reference count becomes 0, the resources pointed to will be released automatically. It has a get() method that can return its saved original pointer (C pointer). It is used as an "Observer" to compare whether two objects are the same - never save it unless you like dangling pointers.

Obviously, based on the expressive power of modern C + +, we can confidently choose any scheme; Here we choose the latter: use a separate tree to save the pointer to the Actor. This choice is not out of foresight, but for a very simple reason: it is troublesome to save the Eigen objects (or objects containing them) in the STL container.

Actor class

The Actor class is sealed. When it is constructed, it will construct its own Transformer object to save its position and posture information in the scene; In addition, it has two important functions:

1. As the node of the scene tree, it provides the ability to manage the dependency relationship between actors (create child nodes, recursively delete itself and all its child nodes), which is completed in cooperation with the Hierarchy scene tree class in the following text
2. As the carrier of Role, it provides the ability to control the whole life cycle of Role

First give the summary of Actor class:

// File: core.hpp

class Actor final : public std::enable_shared_from_this<Actor> {
    friend class Hierarchy;
    friend class Role;

private:
    Hierarchy* _hierarchy { nullptr };
    std::unique_ptr<Transformer> _transformer { nullptr };
    std::string _name {};
    std::shared_ptr<Actor> _parent { nullptr };
    std::list<std::weak_ptr<Actor>> _children {};
    std::vector<std::unique_ptr<Role>> _roles {};

    Hierarchy::registry::iterator findSelfInRegistry() const;
    void refreshChildren();

public:
    Actor() = default;
    Actor(Hierarchy* hierarchy, const char* name):
        _hierarchy(hierarchy),
        _transformer(new Transformer),
        _name(name) {}
    Actor(Hierarchy* hierarchy, const char* name, std::unique_ptr<Transformer>&& transformer):
        _hierarchy(hierarchy),
        _transformer(std::move(transformer)),
        _name(name) {}
    Actor(Actor&& source) noexcept:
        _hierarchy(source._hierarchy),
        _name(std::move(source._name)) { _transformer.swap(source._transformer); }
    Actor& operator=(Actor&& source) noexcept {
        if (&source != this) {
            _hierarchy = source._hierarchy;
            _transformer.reset();
            _transformer.swap(source._transformer);
            _name = std::move(source._name);
        }
        return *this;
    }
    Actor(const Actor&) = delete;
    Actor& operator=(const Actor&) = delete;
    ~Actor();

    std::shared_ptr<Actor> refer();
    std::shared_ptr<const Actor> refer() const;
    std::weak_ptr<Actor> referWeak();
    std::weak_ptr<const Actor> referWeak() const;
    std::shared_ptr<Actor> destroy();

    const Transformer& getTransformer() const;
    Transformer& getTransformer();
    Eigen::Affine3f getWorldSpaceTransform() const;
    Eigen::Vector3f getWorldSpacePosition() const;

    const std::string& getName() const;
    Actor& setName(const char* name);

    Actor& getParent();
    const Actor& getParent() const;
    Actor& setParent(Actor& actor);
    auto getChildren() const;
    auto getChildren();
    Actor& createChild(const char* name);

    auto getRoles() const;
    auto getRoles();
    template <typename Derived>
    Derived& findRole();
    template <typename Derived>
    auto findRoles();
    Role& attachRole(std::unique_ptr<Role>&& role, bool activate = true);
    template <typename T, typename... Types>
    T& attachRole(bool activate, Types&& ... ctor_args);
    template <typename T, typename... Types>
    T& attachRole(Types&& ... ctor_args);
};

The definitions of friend classes Hierarchy and Role will be given below; auto as the return value type is a C++14 feature, which tells the compiler to infer the return value type of the function from the return of the function body; If there are multiple return paths in the function body, any one different from others will cause the program to fail to compile.

The reason for using this feature here is simple: the type name of the returned value is too long (for example, _remapimpl < STD:: List < STD:: pair < const STD:: string, STD:: shared_ptr < actor > >, STD:: allocator < STD:: pair < const STD:: string, STD:: shared_ptr < actor > >:: iterator, actor & >)!

The Actor class actually implements a self maintaining tree. The more important methods are:

• Disable copy constructors and copy assignment operators to avoid unexpected copies (explained later)

• findSelfInRegistry (private method): find the iterator pointing to itself from the scene tree. It is a bridge to establish the connection between Actor and Hierarchy. Because the "Registry" (a member of Hierarchy, which is used to map all actors to their names many to one) here is implemented by hash table, Therefore, the lookup operation has constant time complexity (when there are no duplicate actors in the scene) or linear time complexity (increases with the increase of the number of duplicate actors)

• Refer, referbreak: because we use smart pointers to operate actors, and the necessary condition for the normal operation of smart pointers is the continuous transfer of ownership, that is, there must be a "space-time path" (direct or indirect transfer of a series of values in the past or in the future) between any two smart pointers holding the same resource, so as to make the ownership traceable. To ensure this while taking into account the execution efficiency, it is generally difficult for us to implement it through conventional programming, so we inherit STD:: enable for the Actor class_ shared_from_this to obtain the function shared provided by the standard library_ from_ This and weak_from_this enables the Actor to generate a shared with correct ownership at any time_ PTR or weak_ptr points to itself; Then we wrap these two functions with refer and refweek

  Notice this strange syntax: class actor: public STD:: enable_ shared_ from_ This < actor >, which seems to "inherit itself", is called "curiously recursive template pattern (CRTP). It does not violate any existing C + + syntax and is a long-standing C + + static polymorphism technique; In addition, it must be public inheritance, otherwise shared will be called_ from_ STD:: bad thrown when this()_ weak_ PTR (attempt to lock the released weak pointer).

• createChild: create its own child Actor and automatically register it in the scene tree; The child Actor and itself are two-way links, which will lead to the problem of circular reference of pointers. Therefore, we design: weak pointers (std::weak_ptr) are used from the parent Actor to the child Actor, and strong pointers (std::shared_ptr) are used from the child Actor to the parent Actor, so as to ensure the unidirectionality of reference count and avoid memory leakage

• refreshChildren (private method): due to the existence of weak pointers, when performing operations such as "get all child actors", you need to "lazily" maintain the Children linked list and delete the released child actors

• getChildren: get a container from which all child actors can be iterated; Because all actors use shared_ptr controls the release, that is, the pointer is saved in the container, but we hope that on the call side, we can directly obtain the instance reference of the child Actor by accessing the container (for example, through the range for loop) to achieve the purpose of "transparency" API, so we need to implement this method through a custom iterator; The specific implementation uses slightly complex generic techniques, which are not described in detail here, but only the source code:

      auto getChildren() {
          refreshChildren();
          return make_remap(_children.begin(), _children.end(),
              [](const std::list<std::weak_ptr<Actor>>::iterator& it) -> Actor& {
                  if (auto locked = it->lock()) { return *locked; }
                  throw std::logic_error("Actor::getChildren: accessing expired child");
              });
      }
  

  Make here_ Remap is a global function implemented by us. It accepts 3 ~ 4 parameters, which are as follows:

  1. Section start iterator
  2. End position iterator for section
  3. Container's trailing iterator (optional, useful when the second parameter is not the container's trailing iterator)
  4. A mapping function is a pointer or reference to a static function (global function or static method), or an imitation function of a static overload (), or a non captured Lambda. It accepts iterator references of the same type as the above parameters and returns the element references to be finally exposed to the call side - when the mapping function uses Lambda, the parameter type cannot be written to auto, Although it can be deduced theoretically (I really can't extract this parameter type!); It is also recommended to specify the return type to prevent implicit copying (as mentioned earlier, we deleted the copy constructor of Actor class, which is mainly for this reason. After deletion, if the Lambda does not specify the return type, it will cause a compilation error: try to use the deleted function, and you will have one product)

  The function returns a special "container", which can iterate all elements within the specified range of the first parameter (including) and the second parameter (excluding), and how to provide these elements is given by the mapping function; The "container" does not store any actual elements and is a "remapping" of the original container.

• setParent: used to set the parent Actor of the Actor. This is a class that needs special care when writing. See its implementation:

  inline Actor& Actor::setParent(Actor& actor) {
      // Acceptable exception
      if (_parent.get() == &actor) { return *this; }
  
      // The very dangerous exception
      if (_hierarchy != actor._hierarchy) { throw std::logic_error("..."); }
  
      // Other unacceptable exceptions
      if (this == _hierarchy->_root.get()) { throw std::runtime_error("..."); }
      if (this == &actor) { throw std::runtime_error("..."); }
  
      // Delete self from parent's children
      _parent->refreshChildren();
      auto& old_children = _parent->_children;
      old_children.erase(std::find_if(old_children.begin(), old_children.end(), [this](const std::weak_ptr<Actor>& ptr) {
          return ptr.lock().get() == this;
      }));
  
      // Reset parent
      if (_hierarchy->_root.get() == &actor) {
          _parent = _hierarchy->_root->shared_from_this();
      } else {
          _parent = actor.shared_from_this();
      }
  
      // Add self to new parent's children
      _parent->_children.emplace_back(weak_from_this());
      return *this;
  }
  

  We first exclude several special cases:

  1. If the new parent node is the same as the original parent node, you don't have to do anything (the only non dangerous special case)
  2. If the new parent node is not in the same scene tree as the current node, it will be rejected. We will not take care of the affairs of multiple scenes for the time being (special cases that are easy to ignore and there is a risk of memory leakage)
  3. If the current node is the root node of the scene tree, it is rejected because the root node cannot have a parent node (we do not consider operations such as tree rotation - this is only a scene tree with a fixed structure)
  4. If the new parent node is the current node, reject it (this is also an easily ignored special case, which will generate a circular reference of the current node to itself, which can lead to memory leakage)

  Next, we should first conceive: what steps are required to complete the operation of replacing the parent node?

  1. First, delete yourself from the child node set of the original parent node;
  2. Then replace your parent node with a new one. The reference count of the original parent node is - 1 and the reference count of the new parent node is + 1;
  3. Finally, add yourself to the child node set of the new parent node.

• Destroy: destroy the Actor itself, which is also a method that needs to be written carefully. First of all, it needs to be clarified that it is different from the destructor:

  • destroy ends the Actor's life cycle at the program level, that is, it and all child actors are removed from the scene tree, and its own roles become invalid;
  • Destructors end the life cycle of objects at the language level. They control the shared of resources used by actors_ PTR is automatically called when the reference count becomes 0 to avoid dangling pointers and memory leaks.

  After understanding the above differences, we can sort out the steps to "clean" destroy an Actor:

  1. Deconstruct all the roles it mounts, thus ending all functions in the program
  2. Dereference parent Actor
  3. Call destroy of all child actors to achieve recursive destruction
  4. From the scene tree, select the shared that controls its own life cycle_ PTR is copied to the local part (the reference count is 2 at this time) and deleted from the scene tree (the reference count is 1), and its ownership will return to the local part - this is a key step. If you don't keep a shared in the local part temporarily_ PTR, it may be destructed before the destroy function returns (since the current Actor will not access any resources later, even if "early destruct" occurs, the problem is too big, but it is an undefined behavior after all)
  5. Return its own shared_ptr, whose reference count is 1
  6. With the returned shared_ptr is destructed on the calling side (as a temporary variable) and its own shared_ptr reference count reaches 0, and it is destructed

  In fact, console output cannot be carried out in the destructor (any operation that may throw an exception cannot be carried out, because the destructor has an implicit noexcept modifier, and the thrown exception cannot be captured and processed, which will directly kill the main thread), but we add a print for the convenience of testing.

• getRoles: similar to getChildren, we also use some techniques to return a container map that can directly iterate out the Role (component) instance;

• findRole, findRoles: Here we use C + + RTTI (which can be understood as lightweight reflection) to find the required derived types of roles from all roles of Actor; The former returns the reference of the first instance found (throw an exception if it is not found), and the latter returns a vector containing the references of all the instances found. The implementation is as follows:

  template <typename Derived>
  Derived& findRole() {
      for (auto& it : _roles) {
          auto& ref = *it;
          if (typeid(ref) == typeid(Derived)) { return dynamic_cast<Derived&>(ref); }
      }
      throw std::runtime_error("Actor::findRole: cannot find the required role");
  }
  template <typename Derived>
  auto findRoles() {
      std::vector<std::reference_wrapper<Derived>> result;    // Not vector<Derived&> !!
      for (auto& it: _roles) {
          auto& ref = *it;
          if (typeid(ref) == typeid(Derived)) { result.emplace_back(dynamic_cast<Derived&>(ref)); }
      }
      return result;
  }
  

  It should be noted that although C + + does not have reflective runtime support (type_info only stores a small amount of metadata such as enumeration values and type names), RTTI is still a slightly expensive technology (it needs to query global type_info objects, which has additional computational overhead). Therefore, it should be used as little as possible, especially in the loop.

  To use RTTI, you need to import the header file < TypeInfo >, and use reference_wrapper needs to import header file < functional >.

• attachRole: we want each Actor to own all its roles exclusively (an Actor obviously should completely determine the life cycle of his Role!), So use unique_ptr to manage Role resources; We allow two ways to create roles:

  1. Unique passed directly into Role_ The right value reference of PTR pointer (optionally, the last parameter is Boolean, which controls whether to activate the Role immediately), which is equivalent to the calling side "completely abandoning the ownership of the Role and handing it over to the current Actor"
  2. Directly pass in all the arguments of the Role constructor, just like calling its constructor (optionally, the first parameter is Boolean, which controls whether to activate the Role immediately). This is realized by relying on the deformable parameter table template of C++11 and perfect forwarding (std::forward)

  When a Role is added to the Actor, it unconditionally calls its onAttach method (see below) and its onActivate method as needed (if activated immediately).

  You may notice that we didn't write classes like detachRole, which is a design choice because we don't intend to expose our own_ roles container to the outside (this is dangerous). We choose to add the detach method to the Role later and let it unbind itself from the Actor, which is consistent with the concept of Actor::destroy.

The Actor class also provides two important methods that allow us to obtain the world coordinates of an Actor in a long Actor relationship chain:

• getWorldSpaceTransform: get the transformation matrix from the origin of the world coordinate (the M matrix used to pass in the V shader). This function needs to wrap its own Transformer::getTransform and roam the Actor relationship chain where it is located. The reference implementation is as follows (I don't want to add a cache mechanism to it because it's too troublesome):

  inline Eigen::Affine3f Actor::getWorldSpaceTransform() const {
      Eigen::Affine3f m(_transformer->getTransform());
      auto actor = _parent;
      while (actor != _hierarchy->_root) {
          m = actor->_transformer->getTransform() * m;
          actor = actor->_parent;
      }
      return m;
  }
  

• getWorldSpacePosition: obtain its absolute coordinates in the world coordinate system (not the transformation matrix), but we don't save this thing in the Transformer (because we can't do it). What should we do? Simply multiply the result of getWorldSpaceTransform by a homogeneous coordinate vector of the world coordinate origin, and then take the first three dimensions:

  inline Eigen::Vector3f Actor::getWorldSpacePosition() const {
      return (getWorldSpaceTransform() * Eigen::Vector4f::UnitW()).head(3);
  }
  

So far, we have written a basic class with rich functions and high cohesion, which can reduce the complexity of subsequent development.

Hierarchy class

Hierarchy is also sealed (I can't think of any use in inheriting it!), It works with the Actor class, so it is friends with each other. Our great Actor class has implemented many important functions, so hierarchy needs to do less. The following is its summary:

// File: core.hpp

class Hierarchy final {
    friend class Actor;
    using registry = std::unordered_multimap<std::string, std::shared_ptr<Actor>>;

private:
    registry _registry {};
    std::shared_ptr<Actor> _root;

public:
    static constexpr char* ROOT_ACTOR_NAME = "HierarchyRoot";

    Hierarchy();
    ~Hierarchy();

    Actor& createActor(const char* name);
    const Actor& findActor(std::string name) const;
    Actor& findActor(std::string name);
    auto findActors(std::string name);
    auto findActors(std::string name) const;

    void doRenderStart();
    void doPreRenderFrame();
    void doRenderFrame();
    void doPostRenderFrame();
    void doRenderEnd();
};

The most important function of Hierarchy is to keep the root node pointer of the scene tree_ Root. In addition, it also maintains (together with the Actor class) a hash table, which stores all actors and their names in the scene, allowing us to simply and quickly traverse the whole scene (tens to hundreds of frames per second, several times per frame!), Or find the Actor with the specified name.

The void functions of the Hierarchy are used to invoke in the rendering loop. They will traverse all the Actor in the whole scene and invoke the corresponding functions of all activated Role on each Actor, thus realizing an event pump.

Role class

Role class is abstract. Its main significance is to give the blueprint of all roles for inheritance. Here is a summary of it:

// File: core.hpp

class Role {
    friend class Actor;

private:
    Actor* _actor { nullptr };
    bool _active { true };

public:
    Role() = default;
    Role(Role&&) = delete;
    Role& operator=(Role&&) = delete;
    Role(const Role&) = delete;
    Role& operator=(const Role&) = delete;
    virtual ~Role() = default;

    bool isActive() const;
    Role& setActive(bool active);
    const Actor& getActor() const;
    Actor& getActor();

    std::unique_ptr<Role> detach();

    virtual void onAttach() {}
    virtual void onActivate() {}
    virtual void onDeactivate() {}
    virtual void onRenderStart() {}
    virtual void onPreRenderFrame() {}
    virtual void onRenderFrame() {}
    virtual void onPostRenderFrame() {}
    virtual void onRenderEnd() {}
    virtual void onDetach() {}
};

Role has status_ Active, which is used to record whether it is currently active or not. The outside world can set it through setActive(active); When the activation status changes, onActivate() or ondectivate() is called:

inline Role& Role::setActive(bool active) {
    if (_active != active) {
        _active = active ? (onActivate(), true) : (onDeactivate(), false);
    }
    return *this;
}

Explain the event functions defined by Role, which are called at the corresponding time, so as to give the component-oriented development model event driven ability. The following is a detailed description:

• onAttach: when a Role is added to the Actor, it is executed unconditionally (whether activated or not)
• onActivate: when a Role is activated, it can be executed after onAttach or when the activation state changes
• onDeactivate: when a Role is disabled, or when an active Role is being destroyed, it is executed before onDetach. A Role that has never been activated will not execute the event function
• onRenderStart: when the rendering cycle starts, if the Role is active, it is executed
• onPreRenderFrame: when preparing to start rendering the current frame, if the Role is active, execute
• onRenderFrame: when rendering the current frame, if the Role is active, it is executed
• onPostRenderFrame: at the end of the rendering of the current frame, if the Role is active, it is executed
• onRenderEnd: when the rendering cycle ends, if the Role is active, it is executed
• onDetach: execute unconditionally when the Role is destroyed (whether activated or not)

——This is only a temporary API plan. If we need more events later, we can continue to define them.

Another method worth mentioning is detach, which "removes" the Role from the Actor and returns the unique point to itself originally held by it_ PTR, so that we can transfer the Role to other actors (it's a bit like an Actor in the theater can't attend temporarily, so we hand over his Role to other actors); Because of the unique_ptr is the right value returned by the function. Therefore, if the caller of detach does not assign it to any variable, it will be naturally destructed as a temporary quantity after the call (the whole process is smooth, too elegant and intoxicated):

inline std::unique_ptr<Role> Role::detach() {
    std::unique_ptr<Role> me(nullptr);
    for (auto it = _actor->_roles.begin(), last = _actor->_roles.end(); it != last; ++it) {
        if (it->get() == this) {
            me.swap(*it);
            _actor->_roles.erase(it);
            break;
        }
    }
    if (me == nullptr) { throw std::logic_error("Role::detach: cannot find self in actor's roles"); }
    setActive(false);
    onDetach();
    _actor = nullptr;
    return me;
}

Test actor role model

After the framework is written, we can derive a useless Role to test the function of Role:

class FooRole : public Role {
private:
    std::string _name {"ObscureFooRole"};

public:
    FooRole() = default;
    FooRole(const char* name) : _name(name) {}
    ~FooRole() override { std::clog << _name << " freed" << std::endl; }

    void onAttach() override { std::clog << _name << " onAttach" << std::endl; }
    void onActivate() override { std::clog << _name << " onActivate" << std::endl; }
    void onDeactivate() override { std::clog << _name << " onDeactivate" << std::endl; }
    void onRenderStart() override { std::clog << _name << " onRenderStart" << std::endl; }
    void onPreRenderFrame() override { std::clog << _name << " Pre! "; }
    void onRenderFrame() override { std::clog << _name << " Render! "; }
    void onPostRenderFrame() override { std::clog << _name << " Post! "; }
    void onRenderEnd() override { std::clog << _name << " onRenderEnd" << std::endl; }
    void onDetach() override { std::clog << _name << " onDetach" << std::endl; }
};

The function of FooRole is very simple, which is to print strings when each event occurs.

Next, test in the Application class. First, add the Hierarchy object in the class member declaration and initialize it in the constructor:

// File: application.hpp

...

// In class Application:
class Application {
protected:
    Hierarchy _scene {};

    ...

    // Add protected Application::setupScene:
    virtual void setupScene() {
        _scene.createActor("Foo").attachRole<FooRole>();    // Make an actor and give it a role
    }

    ...

    // In Application::ctor:
    Application(int width, int height, const char* title = "GLFW") {
        
        ...

        // Setup scene
        setupScene();
    }

Next, we rewrite the rendering loop of Application and call the five do provided by Hierarchy Interface:

// File: application.hpp

...

// In Application::renderLoop:
virtual void renderLoop() {
    glThrow("when entering render loop");
    std::uint64_t i = 0;
    _scene.doRenderStart();             // Calling doRenderStart
    while (!glfwWindowShouldClose(_window)) {
        putchar('\r');                  // Avoid swiping the screen
        handleInput();
        _scene.doPreRenderFrame();      // Adjust doPreRenderFrame
        renderFrame();                  // doRenderFrame will be called in renderFrame
        printf("Frame: %lld ", ++i);    // Printout frame number
        _scene.doPostRenderFrame();     // Call doPostRenderFrame
        glfwPollEvents();
        glfwSwapBuffers(_window);
    }
    putchar('\n');
    _scene.doRenderEnd();               // Calling doRenderEnd
}

// In Application::renderFrame:
virtual void renderFrame() {
    // Clear frame
    glClearColor(0.3f, 0.3f, 0.3f, 1.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    _scene.doRenderFrame();

    ...

Run the program and observe the output of the console. For example, close the program when the program renders 200 frames. You will see such console history:

ObscureFooRole onAttach
ObscureFooRole onActivate
ObscureFooRole onRenderStart
ObscureFooRole Pre! ObscureFooRole Render! Frame: 200 ObscureFooRole Post!
ObscureFooRole onRenderEnd
ObscureFooRole onDeactivate
ObscureFooRole onDetach
ObscureFooRole freed

The obseurefoorole here is the default name of FooRole. We will try to call the parameter constructor of FooRole when attachrole < FooRole > to give our FooRole a (famous) Name:

    virtual void setupScene() {
        _scene.createActor("Foo").attachRole<FooRole>("DonQuixote");
    }

Running the program, you can see the exciting plot: at the end of the story, "the great Raman Knight" is finally free (FOG).

Camera as Role

With Role, any program entity can be elegantly coupled with space—— A yuan

We can finally safely and boldly implement a component Camera. The following is a summary of the Camera class:

// File: camera.hpp

class Camera : public Role {
protected:
    std::weak_ptr<const Actor> _focus {};
    float _roll { 0.f };

    mutable Eigen::Matrix3f _coord { Eigen::Matrix3f::Identity() };
    mutable Eigen::Matrix4f _view { Eigen::Matrix4f::Identity() };

    void updateView() const;

public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    Camera() = default;
    Camera(const Actor& focus, float roll_deg):
        _focus(focus.referWeak()),
        _roll(to_rad(roll_deg)) {}
    explicit Camera(const Actor& focus):
        Camera(focus, 0.f) {}
    ~Camera() override = default;

    void onPreRenderFrame() override;

    Camera& lookAt(const Actor& focus);
    float getRoll() const;
    Camera& setRoll(float roll_deg);
    Camera& addRoll(float roll_deg);

    Eigen::Vector3f getXAxis() const;
    Eigen::Vector3f getYAxis() const;
    Eigen::Vector3f getZAxis() const;
    const Eigen::Matrix3f& getViewCoordinates() const;
    const Eigen::Matrix4f& getViewMatrix() const;
    virtual const Eigen::Matrix4f& getProjectionMatrix() const = 0;
};

Camera is the first useful Role we wrote, but it cannot be instantiated directly because it is abstract. This is due to a simple consideration: there are different projection forms. Therefore, we need to continue to derive the camera class and rewrite getProjectionMatrix to return the specific projection.

• _ focus: it is a weak pointer to the Actor that the camera is looking at. The reason for using the weak pointer here is that we don't want the camera to affect the Actor's life cycle (it's hard to imagine that the photographer actually owns the ownership of the Actor on the stage!). We check the availability of the weak pointer in each frame. If it is available, it means that the watched Actor still exists in the world. Then we lock the weak pointer briefly and obtain the world space coordinates of the target Actor, so as to calculate the line of sight vector and update the observation matrix; If it is not available, it means that the staring Actor no longer exists. At this time, we do nothing (do not update the observation matrix) until another Actor is designated as a new staring target

• _ Roll this is the roll angle of the camera, that is, the rotation angle of the camera along the line of sight. It is one of the three Euler angles, which is necessary to realize. Here, we will explain this necessity in the "roll angle" section later; Now we don't need to care too much about it

• lookAt: just reset_ focus to another Actor

• The member modified by mutable keyword can be modified in const method. It generally modifies members that "will not affect the key internal state of the class when changed, may be modified at any time, and are temporary", such as members used to implement a certain caching mechanism in the class to improve operation efficiency, or members that provide certain debugging auxiliary information, etc_ coord is the cache of the matrix (the base matrix of the observation space) laterally arranged by the three column vectors of the camera's right axis (X axis), upper axis (Y axis) and line of sight axis (Z axis, that is, the axis coincident with the line of sight and pointing from the target to the camera)_ Views are caches of observation matrices - we want them to be updated in a const Camera, so we declare them mutable

• onPreRenderFrame: rewrite the Role event handling method. The content is very simple, that is, wrap updateView

• getViewMatrix: it is also very simple and returns directly_ view

• updateView (protection method): This is the "highlight" of the Camera class. It is only called by onPreRenderFrame to update the observation matrix. Let's explain its implementation:

  inline void Camera::updateView() const {
      if (auto locked = _focus.lock()) {
          // Calculate Z
          auto pos = getActor().getWorldSpacePosition();
          _coord.col(2) = (pos - locked->getWorldSpacePosition()).normalized();
          locked.reset();
  
          // Calculate X
          _coord.col(0)(0) = cos(_roll) * _coord.col(2)(2);
          _coord.col(0)(1) = -sin(_roll) * _coord.col(2)(2);
          _coord.col(0)(2) = sin(_roll) * _coord.col(2)(1) - cos(_roll) * _coord.col(2)(0);
          _coord.col(0).normalize();
  
          // Calculate Y
          _coord.col(1) = _coord.col(2).cross(_coord.col(0));
  
          // Calculate view matrix
          for (int i = 0; i < 3; ++i) {
              _view(0, i) = _coord.col(0)(i);
              _view(1, i) = _coord.col(1)(i);
              _view(2, i) = _coord.col(2)(i);
          }
          _view(0, 3) = -_coord.col(0).dot(pos);
          _view(1, 3) = -_coord.col(1).dot(pos);
          _view(2, 3) = -_coord.col(2).dot(pos);
      }
  }
  

  Here_ coord.col(0) indicates_ The first column of the coord matrix, i.e. the X-axis (right axis) of the observation space; The Y and Z axes are the same.

  1. First we try to lock it_ focus, if it is not locked (which means _focushas been released), do nothing and return directly; Otherwise, proceed
  2. Calculate the line of sight axis. According to the vector subtraction, we know that its direction is equal to the direction of the difference vector from the camera coordinate to the target coordinate; Because it is a unit vector, it also needs normalization
  3. Release_ focus, we don't need it anymore
  4. There are two algorithms for calculating the right vector:
     1. If we don't consider the roll angle of the camera, we can use a more efficient method to calculate the right vector: (in the world coordinate system) the X coordinate of the right axis is the Z coordinate of the line of sight axis, the Y coordinate of the right axis is 0, the Z coordinate of the right axis is the X coordinate of the line of sight axis, and then normalize the generated rear axis, It should be noted here that if the right axis mode length before normalization is very small, Eigen will not do any processing, so it will not lead to division 0 error or maximum floating-point number problem;
     2. Because we want to consider the rolling angle, we still use the "mathematically correct" method in the textbook: cross multiply the line of sight vector with the Y axis (pointing to the zenith) of the world coordinate system, normalize it, and then take the inverse; Of course, this method can also be optimized into an equation, but personally it doesn't make much sense.
  5. Calculate the upper vector. Since the observation space and world space are both right-handed systems, the upper vector is the cross product of the line of sight axis and the right axis; Since the other two axes are unit vectors, the cross product must be unit vectors, so we don't need to normalize the upper vector
  6. Finally, the observation matrix is calculated according to the three axes of the observation space coordinates and the position of the camera itself

Next, we derive a Camera for perspective projection:

class PerspectiveCamera : public Camera {
private:
    float _fov { to_rad(45.f) };
    float _aspect { 1.f };
    float _near { .1f };
    float _far { 100.f };

    mutable Eigen::Matrix4f _proj { Eigen::Matrix4f::Zero() };

    void updateProjection() const;

public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    PerspectiveCamera() {
        _proj(3, 2) = -1.f;
        updateProjection();
    }
    explicit PerspectiveCamera(const Actor& focus, float fov = to_rad(45.f), float aspect = 1.f, float near = .1f,
        float far = 100.f, float roll_deg = 0.f)
        :
        Camera(focus, roll_deg), _fov(fov), _aspect(aspect), _near(near), _far(far) {
        _proj(3, 2) = -1.f;
        updateProjection();
    }
    ~PerspectiveCamera() override = default;

    const Eigen::Matrix4f& getProjectionMatrix() const override;

    PerspectiveCamera& setFieldOfView(float fov);
    float getFieldOfView() const;
    PerspectiveCamera& setAspect(float aspect);
    float getAspect() const;
    PerspectiveCamera& setClipPlanesDepth(float near, float far);
    float getNearClipPlaneDepth() const;
    float getFarClipPlaneDepth() const;
};

The formula of perspective projection matrix has been given in the previous article. What we do here is to dynamically update it. When the parameters do not change, it will not be updated. When the parameters change, only the coefficients related to the changed parameters in the projection matrix will be updated without regenerating or updating the whole matrix, so as to improve the operation efficiency.

Operation in constructor_ proj(3, 2) = -1.f; The meaning is, because_ Proj is initially a full zero matrix, and the elements of the matrix in the formula ( 4 , 3 ) (4, 3) (4,3) is equal to - 1, so it is only written once during initialization, and the element will not be updated later.

Slightly complex scene

With the camera, we can shuttle through the scene at will. Let's make a more complex scenario:

1. Add the parent objects of all renderable objects in the scene, and add a bunch of block actors with random positions, sizes and poses
2. Add a pair of "planet satellite" boxes, where the "planet" box is located near the center of the scene, and the "satellite" box is the sub Actor of the "planet" box, so as to test whether the transformation matrix of the multi-level Actor works normally
3. Add the rotation axis Actor of the camera (we use it to quickly realize the rotation of the camera around a point without calculating the specific coordinates such as sin. Add the sub Actor carrying the camera on the rotation axis and add a perspective camera for it. The observation target of the camera is the "planet" box

setupScene method:

    virtual void setupScene() {
        // Base actor of all cubes
        auto& base = _scene.createActor("Cubes");

        // Random cubes
        std::mt19937 gen(19980414);
        std::uniform_real_distribution<float> random(-5, 5);
        int cubes = 10;
        char name[10] = "";
        for (int i = 0; i < cubes; ++i) {
            sprintf_s(name, "Cube%d", i);
            base.createChild(name).getTransformer()
                .setPosition(random(gen), random(gen), random(gen))
                .setRotation(float(gen() % 90), Eigen::Vector3f::Random())
                .setScale((random(gen) + 5.5f) / 4.f);
        }

        // Ground is a stretched cube
        // base.createChild("Ground").getTransformer().setScale(50.f, 0.f, 50.f).setPosition(-1.f, 0.f, -1.f);

        // Planet-satellite cubs
        auto& bc = base.createChild("CenterCube");
        bc.createChild("SmallCube").getTransformer().setPosition(8.f, 0.f, 0.f);

        // Camera
        auto& camera = _scene.createActor("CameraPivot").createChild("Camera");
        camera.getTransformer().setPosition(0.f, 5.f, 10.f);
        camera.attachRole<PerspectiveCamera>(bc);
    }

std::mt19937 gen(19980414); The magic number in this sentence is a random number seed. When the seed is certain, we can get a certain result every time we run, so as to realize the reproducibility of the scene.

The position update timing of the camera and moving object is set at the handleInput executed in each frame. This has additional benefits (which will be shown later). Since we already have an elegant API to operate the position of the Actor, we rewrite it as follows:

    virtual void handleInput() {
        if (glfwGetKey(_window, GLFW_KEY_ESCAPE)) {
            glfwSetWindowShouldClose(_window, true);
        } else {
            _scene.findActor("Camera").findRole<PerspectiveCamera>().setAspect(getAspectRatio());

            GLfloat t = (GLfloat)glfwGetTime();
            _scene.findActor("CenterCube").getTransformer()
                .setPosition(0.f, 2.5f * sin(.5f * t), 0.f);
            _scene.findActor("SmallCube").getTransformer()
                .setRotation(180.f * t, Eigen::Vector3f {1.f, 1.f, 1.f})
                .setPosition(8.f * cos(to_rad(50.f * t)), 0.f, 8.f * sin(to_rad(50.f * t)));
            _scene.findActor("CameraPivot").getTransformer()
                .setRotation(30.f * t, Eigen::Vector3f::UnitY());
            _scene.findActor("Camera").getTransformer().setPosition(0.f, 5.f, 15.f + 10.f * sin(t));
        }
    }

Here, we realize the rotation of the camera around the field by setting the rotation for the CameraPivot; The position set for the camera itself is relative to CameraPivot, so the camera lens can be closer and farther.

Next, modify the rendered frame method:

    virtual void renderFrame() {
        // Clear frame
        ...

        _scene.doRenderFrame();

        // Use VAO, Shader and textures
        ...

        // Set uniforms
        ...

        auto& camera = _scene.findActor("Camera").findRole<PerspectiveCamera>();
        _spo->uniforms["view"] = camera.getViewMatrix();
        _spo->uniforms["projection"] = camera.getProjectionMatrix();

        // Additional operation
        ...

        // Draw calls
        for (auto& cube: _scene.findActor("Cubes").getChildren()) {
            _spo->uniforms["model"] = cube.getWorldSpaceTransform();
            glDrawElements(GL_TRIANGLES, 36, GL_UNSIGNED_INT, nullptr);
        }
        for (auto& cube: _scene.findActor("CenterCube").getChildren()) {
            _spo->uniforms["model"] = cube.getWorldSpaceTransform();
            glDrawElements(GL_TRIANGLES, 36, GL_UNSIGNED_INT, nullptr);
        }
    }

By running the program, we will travel through a world with many squares:

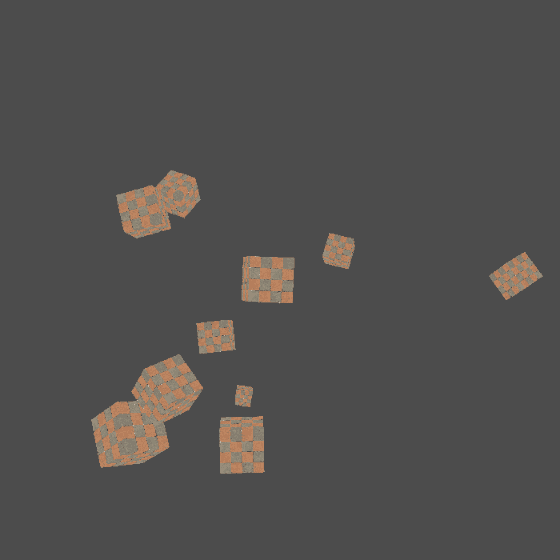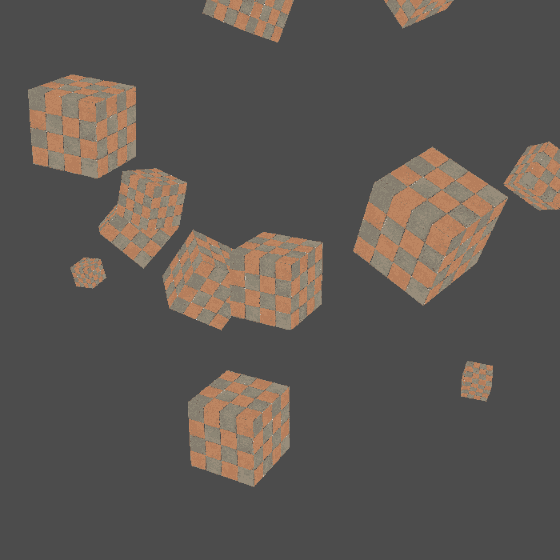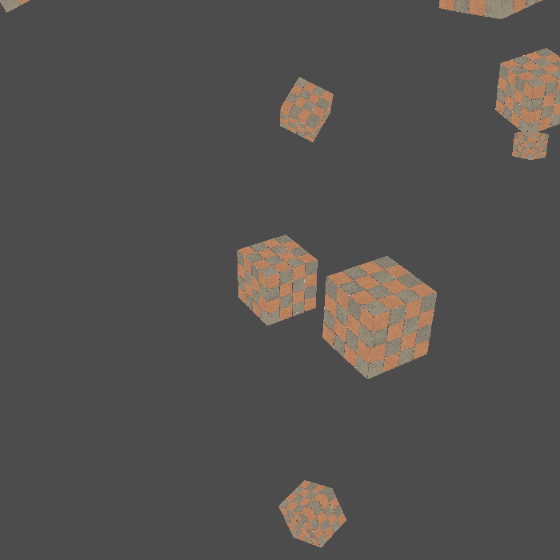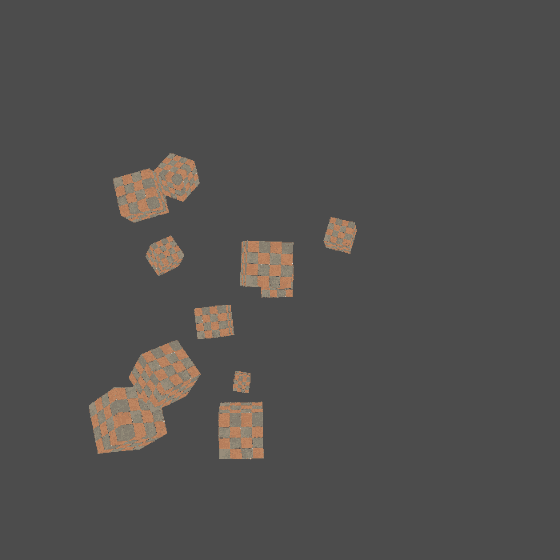
Free camera

We can completely realize the free Camera on the basis of the existing code: just set a virtual gaze target moving with the Camera (it's not so easy to realize the free Camera first and then the target Camera!) In fact, game forms such as FPS may need this Camera more. Before implementation, we first consider some mathematical foundations and transform our Camera class.

Attitude angle

For a free object in space, there are many ways to describe its attitude. We have contacted the transformation matrix; Next, the concept of attitude angle is introduced. The attitude of an object in three-dimensional space can be described by three angles, namely pitch, yaw and roll. Their meaning is shown in the following figure:

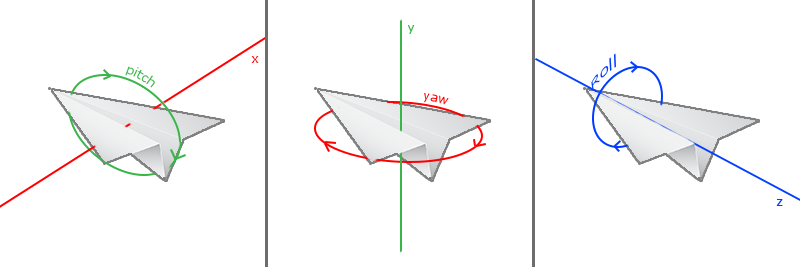
Roll angle

The roll angle is reflected in the camera, that is, the tilt angle of the camera itself - when you tilt your head to one side (not turning your head, nor looking up or down), the roll angle of your eyes as a "camera" changes.

We cannot describe the angle of rotation around the axis by the position of the end of the axis. The reason is obvious: no matter how you rotate, the end of the axis will not move. Since the camera has a line of sight axis, the most special of the above three attitude angles is the roll angle - which cannot be set by looking at the target. We must consider the roll angle when generating the three axes of the observation space.

For the above reasons, our_ Roll is written in the Camera class, which provides setter s and getter s for roll angles; We also use the vector cross multiplication method to calculate the right axis of the observation space (see the previous article for details).

Pitch angle and yaw angle

Since only free cameras have pitch angle and yaw angle, we design a separate class for them to expand Camera and increase its free movement ability:

template <class ConcreteCamera>
class Cameraman : public Role {
private:
    ConcreteCamera* const _camera { nullptr };
    std::unique_ptr<Role> _camera_holder { nullptr };
    std::shared_ptr<Actor> _focus { nullptr };
    float _pitch { 0.f };
    float _yaw { 0.f };

    void updateFocus() const;

public:
    template <typename... Types>
    explicit Cameraman(Types&& ... ctor_args) :
        _camera(new ConcreteCamera(std::forward<Types>(ctor_args)...)),
        _camera_holder(std::unique_ptr<Role> { _camera }) {}
    ~Cameraman() override = default;

    void onAttach() override {
        _focus = getActor().createChild("CameraFocus").refer();
        _camera->lookAt(*_focus);
        updateFocus();
        std::unique_ptr<Role> tmp { nullptr };
        tmp.swap(_camera_holder);
        getActor().attachRole(std::move(tmp));
    }
    void onDetach() override {
        getActor().template findRole<ConcreteCamera>().detach().swap(_camera_holder);
        _focus->destroy();
        _focus.reset();
    }

    float getPitch() const;
    Cameraman<ConcreteCamera>& setPitch(float pitch_deg);
    Cameraman<ConcreteCamera>& addPitch(float pitch_deg);
    float getYaw() const;
    Cameraman<ConcreteCamera>& setYaw(float yaw_deg);
    Cameraman<ConcreteCamera>& addYaw(float yaw_deg);
    float getRoll() const;
    Cameraman<ConcreteCamera>& setRoll(float roll_deg);
    Cameraman<ConcreteCamera>& addRoll(float roll_deg);
    Eigen::Vector3f getWorldRotation() const;
    Cameraman<ConcreteCamera>& setWorldRotation(float pitch_deg, float yaw_deg, float roll_deg);
    Cameraman<ConcreteCamera>& setWorldRotation(const Eigen::Vector3f& pyr_deg);
    Cameraman<ConcreteCamera>& addWorldRotation(float pitch_deg, float yaw_deg, float roll_deg);
    Cameraman<ConcreteCamera>& addWorldRotation(const Eigen::Vector3f& pyr_deg);
    Cameraman<ConcreteCamera>& addViewRotation(float pitch_deg, float yaw_deg, float roll_deg);
    Cameraman<ConcreteCamera>& addViewRotation(const Eigen::Vector3f& pyr_deg);
};

This template class saves the pitch angle and yaw angle, and performs the following operations to complete its functions:

1. When constructing, an object of the type specified by the template parameter ConcreteCamera is generated in the heap (the real type of ConcreteCamera must inherit from the Camera base class; we do not need to write a type trait to restrict this. This is because we use the API provided by Camera. If the inheritance conditions are not met, it obviously cannot be compiled)
2. By_ camera_ The holder exclusively holds the ownership of the above ConcreteCamera object; We also keep a copy of the original pointer_ Camera, which only acts as an observer and does not actually hold resources;
3. In the onAttach event, create a child Actor named CameraFocus for the Actor to which you are bound and set it to_ camera_ The target of the ConcreteCamera held by the holder, and then bind the ConcreteCamera to the Actor to which it is bound
4. As long as we rewrite onAttach, we should logically rewrite onDetach and carry out an opposite process: release the CameraFocus generated by ourselves for the Actor and retrieve the Camera we handed over before. The purpose of doing this is to ensure the continuous transfer of ownership, so as to ensure the release of Camera

The method updateFocus is used to update the position of CameraFocus relative to its own Actor. We need to use the formula to ensure that it will move on the sphere centered on its own Actor:

    void updateFocus() const {
        if (!_focus) { return; }
        const float sin_pitch = sin(_pitch), cos_pitch = cos(_pitch), sin_yaw = sin(_yaw), cos_yaw = cos(_yaw);
        _focus->getTransformer().setPosition(-Eigen::Vector3f { sin_yaw, -cos_yaw * sin_pitch, cos_pitch * cos_yaw });
    }

This formula is easy to deduce: consider it as rotating around two axes respectively, and then multiply the rotation matrix.

Here's an explanation: setWorldRotation and addWorldRotation apply rotation to_ pitch and_ yaw, and addViewRotation applies rotation to the Transformer of the bound Actor, although it seems to be no different

Let's test:

    // In Application::setupScene:
    virtual void setupScene() {
        ...

        // Camera
        auto& camera_actor = _scene.createActor("CameraPivot").createChild("Camera");
        camera_actor.getTransformer().setPosition(0.f, 5.f, 10.f);
        camera_actor.attachRole<Cameraman<PerspectiveCamera>>();
    }

    // In Application::handleInput:
    virtual void handleInput() {
        ...
        
        auto t = (GLfloat) glfwGetTime();
        _scene.findActor("Camera").findRole<PerspectiveCamera>().setAspect(getAspectRatio());
        auto& cameraman = _scene.findActor("Camera").findRole<Cameraman<PerspectiveCamera>>();
        cameraman.setYaw(10.f * sin(t)).setPitch(10.f * sin(2.f * t) - 15.f).setRoll(30.f * sin(.5f * t));
        _scene.findActor("CameraPivot").getTransformer()
        .setRotation(30.f * t, Eigen::Vector3f::UnitY());
        _scene.findActor("Camera").getTransformer().setPosition(0.f, 5.f, 15.f + 10.f * sin(t));
        
        ...

Running the program, we look like taking a roller coaster in the world of squares.

Keyboard controlled movement

With the free camera, we can achieve a "helmet view" similar to that in FPS games. The principle is very simple: in the input processing stage of each frame, we check whether the user pressed some keys (remember glfwGetKey?), If you press it, you can change the angle provided by Cameraman's API or the spatial position of its Actor in the corresponding direction.

However, there is a problem here: different users have different hardware levels, so the number of frames rendered per second is also different; The number of frames that can be rendered per second on the same device also depends on the number of triangles in the scene. We want to be able to move the lens at a constant rate, so we need to calculate a time difference between each frame and the previous frame, and then multiply the time difference by the camera moving speed to obtain the final camera position change.

To make the experience better, we might as well add a "smooth acceleration and deceleration" to the camera, that is, define a maximum speed and an acceleration for all variable speed dimensions (X, Y, Z, Pitch, Yaw and Roll), and change the current speed according to the acceleration at each frame to obtain the smoothing effect.

Define all maximum speeds and accelerations, and define member variables to save the current speed:

// In class Application:
class Application {
protected:
    static constexpr float CAMERA_SPEED_X_MAX = 20.f;
    static constexpr float CAMERA_SPEED_X_ACC = 10.f * CAMERA_SPEED_X_MAX;
    static constexpr float CAMERA_SPEED_Y_MAX = 20.f;
    static constexpr float CAMERA_SPEED_Y_ACC = 10.f * CAMERA_SPEED_Y_MAX;
    static constexpr float CAMERA_SPEED_Z_MAX = 20.f;
    static constexpr float CAMERA_SPEED_Z_ACC = 10.f * CAMERA_SPEED_Z_MAX;
    static constexpr float CAMERA_SPEED_PITCH_MAX = 1.f;
    static constexpr float CAMERA_SPEED_PITCH_ACC = 10.f * CAMERA_SPEED_PITCH_MAX;
    static constexpr float CAMERA_SPEED_YAW_MAX = 1.f;
    static constexpr float CAMERA_SPEED_YAW_ACC = 10.f * CAMERA_SPEED_YAW_MAX;
    static constexpr float CAMERA_SPEED_ROLL_MAX = 60.f;
    static constexpr float CAMERA_SPEED_ROLL_ACC = 10.f * CAMERA_SPEED_ROLL_MAX;
    
    // Camera speeding
    Eigen::Vector3f _camera_speed_pos { Eigen::Vector3f::Zero() };  // Current camera move speed
    Eigen::Vector3f _camera_speed_pyr { Eigen::Vector3f::Zero() };  // Current camera rotate speed

Next, we define the function accelerate to provide smooth acceleration and deceleration:

inline float accelerate(float value, float delta, float spd, float acc, bool cond_positive, bool cond_negative,
    bool fade_in = true, bool fade_out = true, float debounce = 1.f) {
    if (cond_negative) {
        value = fade_in ? std::max(-spd, value - delta * acc) : -spd;
    } else if (cond_positive) {
        value = fade_in ? std::min(spd, value + delta * acc) : spd;
    } else if (abs(value) > debounce && fade_out) {
        value += std::signbit(value) ? delta * acc : -delta * acc;
    } else { value = 0.f; }
    return value;
}

The function has 9 parameters:

1. Value: the value of the speed amount to be applied at the last time
2. delta: the elapsed time from the last time to the present (when this parameter is passed in, it can also be multiplied by a time scaling factor to achieve global speed doubling). This parameter is generally less than 1 (second), because we have to update many frames per second
3. spd: target speed, that is, the maximum speed that can be achieved by acceleration
4. acc: increment of speed in unit delta
5. cond_positive: if this Boolean is true, it will accelerate forward
6. cond_negative: if this Boolean is true, reverse acceleration
7. fade_in: if true, value adopts smooth acceleration when accelerating in the positive and negative directions; Otherwise, value instantly reaches the spd speed in the corresponding direction
8. fade_out: if true, in cond_positive and cond_ When negative is false, smooth deceleration will be performed; Otherwise, decelerate to 0 instantly
9. debounce: due to the error in floating-point number calculation, when the speed is close to 0, the sign will be inaccurate, resulting in the speed being negative or positive ϵ \epsilon ϵ( ϵ \epsilon ϵ Is a smaller value) between "drift"; Debounce is used to eliminate this effect: when the absolute value of speed is less than debounce, the speed is directly set to 0

This is a very common acceleration algorithm. You can understand its process by looking at the code.

Since we use the current time in many places and the time difference from the previous frame to the current frame, we update the time uniformly in the rendering cycle and pay attention to its initialization (only in frame 1):

// In class Application:
class Application {
protected:
    ...

    float _time { 0.f };
    float _delta_time { 0.f };
    
    ...

    void updateTime(bool reset) {
        auto t = (float) glfwGetTime();
        _delta_time = reset ? 0.f : t - _time;
        _time = t;
    }
    
    // In Application::renderLoop:
    virtual void renderLoop() {
        ...

        // Loop
        std::uint64_t i = 0;
        while (!glfwWindowShouldClose(_window)) {
            ...

            updateTime(!i);

            ...
        }
        ...
    }

Next, rewrite handleInput:

	// In Application::handleInput:
	virtual void handleInput() {
        if (glfwGetKey(_window, GLFW_KEY_ESCAPE)) {
            glfwSetWindowShouldClose(_window, true);
        } else {
            auto& camera_actor = _scene.findActor("Camera");
            auto& camera = camera_actor.findRole<PerspectiveCamera>();
            auto& cameraman = camera_actor.findRole<Cameraman<PerspectiveCamera>>();

            // Aspect ratio
            camera_actor.findRole<PerspectiveCamera>().setAspect(getAspectRatio());

            // Camera position & rotation
            camera_actor.getTransformer().addPosition(camera.getViewCoordinates() * _camera_speed_pos * _delta_time);
            cameraman.addViewRotation(_delta_time * _camera_speed_pyr);

            // Accelerate camera
            _camera_speed_pos(0) = accelerate(
                _camera_speed_pos(0), _delta_time, CAMERA_SPEED_X_MAX, CAMERA_SPEED_X_ACC,
                glfwGetKey(_window, GLFW_KEY_D), glfwGetKey(_window, GLFW_KEY_A),
                false, true);
            _camera_speed_pos(1) = accelerate(
                _camera_speed_pos(1), _delta_time, CAMERA_SPEED_Y_MAX, CAMERA_SPEED_Y_ACC,
                glfwGetKey(_window, GLFW_KEY_R), glfwGetKey(_window, GLFW_KEY_F),
                false, true);
            _camera_speed_pos(2) = accelerate(
                _camera_speed_pos(2), _delta_time, CAMERA_SPEED_Z_MAX, CAMERA_SPEED_Z_ACC,
                glfwGetKey(_window, GLFW_KEY_S), glfwGetKey(_window, GLFW_KEY_W),
                false, true);

            // Rotate camera
            _camera_speed_pyr(0) = accelerate(
                _camera_speed_pyr(0), _delta_time, CAMERA_SPEED_PITCH_MAX, CAMERA_SPEED_PITCH_ACC,
                glfwGetKey(_window, GLFW_KEY_UP), glfwGetKey(_window, GLFW_KEY_DOWN),
                true, true);
            _camera_speed_pyr(1) = accelerate(
                _camera_speed_pyr(1), _delta_time, CAMERA_SPEED_YAW_MAX, CAMERA_SPEED_YAW_ACC,
                glfwGetKey(_window, GLFW_KEY_LEFT) || glfwGetKey(_window, GLFW_KEY_Q),
                glfwGetKey(_window, GLFW_KEY_RIGHT) || glfwGetKey(_window, GLFW_KEY_E),
                true, true);
            _camera_speed_pyr(2) = accelerate(
                _camera_speed_pyr(2), _delta_time, CAMERA_SPEED_ROLL_MAX, CAMERA_SPEED_ROLL_ACC,
                glfwGetKey(_window, GLFW_KEY_COMMA), glfwGetKey(_window, GLFW_KEY_PERIOD),
                true, true);
        }
    }

Now you may see the benefits of using the accelerate function (especially its cond_positive and cond_negative parameters): we can use it to easily map keyboard to operation. Just check the keyboard with glfwGetKey - you can even map an operation to multiple keys!

Although there are many codes above, they are easy to understand:

1. See if the ESC key is pressed. If so, prepare to close the window, otherwise continue
2. Refresh the current aspect ratio first
3. Then calculate the new camera position and rotation
4. Finally, check all keys to refresh the current camera speed_ camera_speed_pos and_ camera_speed_pyr

It should be noted that when we translate the camera, we do not want to change its world coordinates, but move the camera relative to the current observation space, so we can't write this:

camera_actor.getTransformer().addPosition( /* identity */ _camera_speed_pos * _delta_time);

To multiply the position of "identity" above by the base matrix of the current observation space (that is, the matrix formed by the three axes of the observation space, see the above), this is one of the reasons why our Camera class chooses to use the matrix to store the coordinate axis vector (another reason is efficiency).

Let's run it. Now the camera won't roam automatically. Instead, we can use WASD to control the camera's forward and backward, left and right translation, R and F to control its vertical rise and fall, Q and E (or left and right keys) to control Yaw, up and down arrows to control Pitch, and comma and period keys to control the camera's roll - just like the spacecraft flight system.

zoom

Finally, we implement the mouse wheel to control the zoom. There are two ways to zoom. One is to use the translation of the camera in the direction of the line of sight axis to get close to or away from the target; The other method does not need to move the camera, but changes the FOV (line of sight angle) of the perspective camera. In perspective amera, we have provided the getter and setter of FOV. What we need to do is call it at the right time.

In GLFW, the mouse wheel operation is an event. It cannot be obtained by checking the keyboard, but to register the callback function of GLFW. We use glfwSetScrollCallback(window, callback) to register the mouse wheel callback for the window of the form; Callback accepts three parameters: form pointer (not used here), horizontal scrolling amount of double type (not used here for touchpad and mouse with 3D wheel), and vertical scrolling amount of double type (that's what we want).

Write a callback using Lambda and put it in the constructor of Application (just put it together with the previous glfwSetFramebufferSizeCallback); But here's a problem. We want to write code similar to the following:

    glfwSetScrollCallback(_window, [this](GLFWwindow*, double, double dy) {
        auto& camera = this->_scene.findActor("Camera").findRole<PerspectiveCamera>();
        double fov = camera.getFieldOfView() - dy;
        if (fov - 1. <= epsilon<double>) { fov = 1.; }
        else if (fov - 90. >= epsilon<double>) { fov = 90.; }
        camera.setFieldOfView((float) fov);
    });

However, the above code cannot be compiled because our Lambda is captured (otherwise the this pointer cannot be used). Therefore, the Lambda is dynamic, just like a member method. It will implicitly carry a pointer this when entering the stack, so it cannot be transformed to the static function pointer required by GLFW.

It doesn't matter if you don't understand the above explanation. In short, you can't use Lambda with capture~

To solve this problem, it is also very simple to statically save a pointer to the current Application object in the Application class - we don't want to run multiple program instances anyway; Even if we do, there are other ways to dynamically change the static pointer.

Append a static member to the Application:

	// In class Application:
	static Application* s_active_instance;

Initialize outside class:

// Global scope:
Application* Application::s_active_instance = nullptr;

Bind in the constructor of Application:

    // In Application::ctor:
    s_active_instance = this;

Then go back to the place where you just set the callback:

    glfwSetScrollCallback(_window, [](GLFWwindow*, double, double dy) {
        if (s_active_instance) {
            auto& camera = s_active_instance->_scene.findActor("Camera").findRole<PerspectiveCamera>();
            double fov = camera.getFieldOfView() - dy;
            if (fov - 1. <= epsilon<double>) { fov = 1.; }
            else if (fov - 90. >= epsilon<double>) { fov = 90.; }
            camera.setFieldOfView((float) fov);
        }
    });

Incidentally, we can also modify the previous glfwSetFramebufferSizeCallback callback to change the "refresh projection matrix aspect ratio" of each frame to be called only when the window size changes, so as to reduce unnecessary performance overhead:

    glfwSetFramebufferSizeCallback(_window, [](GLFWwindow*, int w, int h) {
        glViewport(0, 0, w, h);
        if (s_active_instance) {
            s_active_instance->_scene.findActor("Camera").findRole<PerspectiveCamera>().setAspect((float) w / (float) h);
        }
    });

Finally, let's run it. Now you can zoom the whole picture with the scroll wheel.