Handwritten SLAM notes from zero

Rotation mode conversion

Title 1: the known rotation matrix is defined as rotating 45 ° along the Z axis. Please initialize the rotation vector, rotation matrix, quaternion and Euler angle according to this definition. Please program:

1. The mutual conversion relations of the above four expressions are output, and the correctness is verified by referring to the given results.

2. Assuming that the translation vector is (1,2,3), please output the rotation matrix and the Euclidean transformation matrix composed of the translation matrix, and extract the rotation vector and translation vector according to the Euclidean transformation matrix.
**Knowledge points: * * 1. Learn the four expressions of rigid body rotation in eigen, and be familiar with the mutual conversion relationship between them. 2. Be familiar with the mutual conversion relationship between rotation, translation and Euclidean transformation matrix

Initialization of four rotation modes:

    // initialization

    // Rotation vector (axis angle): rotate 45 ° along the z axis
    Eigen::AngleAxisd rotation_vector(M_PI/4, Eigen::Vector3d(0,0,1));
    cout<<"rotation_vector axis=\n"<<rotation_vector.axis()<<endl;
    cout<<"rotation_vector angles\n"<<rotation_vector.angle()<<endl;

    // Rotation matrix: rotate 45 ° along the z axis
    Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
    rotation_matrix<<
        0.707, -0.707, 0,
        0.707,  0.707, 0,
        0,      0,     1;
    cout<<"rotation matrix=\n"<<rotation_matrix<<endl;

    // Quaternion: rotate 45 degrees along the z axis
    Eigen::Quaterniond quat = Eigen::Quaterniond(0,0,0.383,0.924);  // The assignment method is (w,x,y,z)
    cout<<"Quaternion output mode 1: quaternion=\n"<<quat.coeffs()<<endl;    // The output mode is (x,y,z,w)
    cout<<"Quaternion output mode 2:\tw="<<quat.w()<<"\tx="<<quat.x()
        <<"\ty="<<quat.y()<<"\tz="<<quat.z()<<endl;
    
    // Euler angle: rotate 45 ° along z axis
    Eigen::Vector3d euler_angles = Eigen::Vector3d(M_PI/4,0,0);// The zyx order is the yaw pitch roll order
    cout<<"Euler:yaw pitch roll="<<euler_angles.transpose()<<endl;

Mutual transformation of rotation matrix, quaternion and rotation vector:

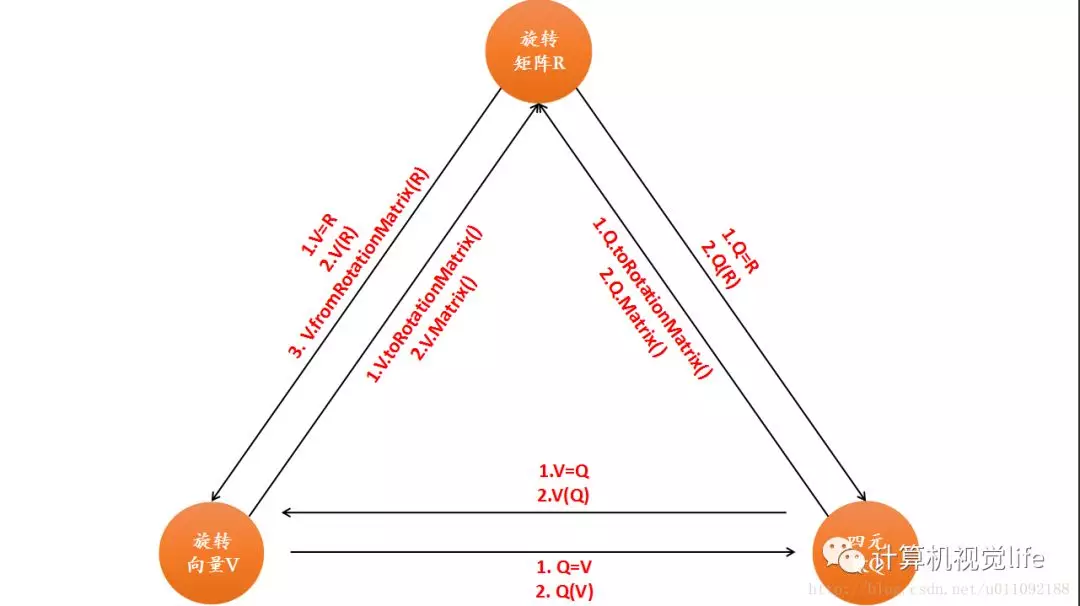
A closer look shows that rotation vectors and quaternions are transformed into rotation matrices. Eigen provides two functions: toRotationMatrix() and Matrix().

For the transformation of rotation matrix into rotation vector, Eigen provides fromRotationMatrix().

The other two can be converted through eg: V=R or V ® There are two ways to assign values.

	// Mutual conversion relationship
    
    // Convert rotation vectors to other forms
    cout<<"Transform rotation vector into rotation matrix method 1: rotation matrix=\n"<<
        rotation_vector.toRotationMatrix()<<endl;
    cout<<"Transform rotation vector into rotation matrix method 2: rotation matrix=\n"<<
        rotation_vector.matrix();
    quat = rotation_vector;
    cout<<"Convert rotation vector to quaternion: quaternion=\n"<<quat.coeffs()<<endl;

    // The rotation matrix is converted to other forms
    cout<<"Convert rotation matrix to rotation vector: rotation_vector axis=\n"<<
    rotation_vector.fromRotationMatrix(rotation_matrix).axis()<<
    "\n rotation_vector angle = "<<rotation_vector.fromRotationMatrix(rotation_matrix).angle()<<endl;
    // The fromRotationMatrix parameter applies only to rotation vectors, not quaternions

    rotation_vector = rotation_matrix;
    cout<<"The rotation matrix directly assigns an initialization value to the rotation vector: rotation_vector angle= \n"<<rotation_vector.angle()<<endl;
    cout<<"rotation_vector axis=\n"<<rotation_vector.axis()<<endl;

    euler_angles = rotation_matrix.eulerAngles(2,1,0); //Difficulty z y x 
    cout<<"The rotation matrix is converted to Euler angles: yaw pitch roll="<<euler_angles.transpose()<<endl;
    quat = rotation_matrix;
    cout<<"Convert rotation matrix to quaternion: quaternion=\n"<<quat.coeffs()<<endl;

    // Convert quaternions to other forms
    rotation_vector = quat;
    cout<<"Convert quaternions to rotation vectors: rotation_vector axis=\n"<<rotation_vector.axis()
        <<"rotation_vector angle=\n"<<rotation_vector.angle()<<endl;
    
    rotation_matrix = quat.toRotationMatrix();
    cout<<"Quaternion to rotation matrix method 1: rotation matrix=\n"<<rotation_matrix<<endl;

    rotation_matrix = quat.matrix();
    cout<<"Quaternion to rotation matrix method 2: rotation matrix=\n"<<rotation_matrix<<endl;

Pay special attention to the transformation of rotation matrix into Euler angle:

euler_angles = rotation_matrix.eulerAngles(2,1,0); //Difficulty z y x 

Parameter 2 1 0 represents Euler angle in the order of z y x, that is, yaw, pitch and roll

Euclidean transformation matrix:

// The Euclidean transformation matrix uses Eigen::Isometry, the affine transformation uses Eigen::Affine3d, and the projective transformation uses Eigen::Projective3d
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();    // initialization
    T.rotate(rotation_vector);
    Eigen::Vector3d v1 = Eigen::Vector3d(1,2,3);
    T.pretranslate(v1);

    cout<<"Transform matrix = \n"<<T.matrix()<<endl;
    cout<<"rotation matrix of T is :\n"<<T.rotation()<<endl;
    cout<<"translation of T is :\n"<<T.translation()<<endl;

Notice that the function that initializes the rotation part of T is rotate(), and the function that outputs the rotation part of T is rotation().

Perception of function naming: it seems that function names such as function assignment generally use verbs, while nouns are used when outputting existing members. This is indeed more logical.

discuss

(refer to planet discussion)
Q:

1. The rotation matrix is directly converted into Euler angle code_ matrix. EulerAngles (2.1.0) what does 2,1,0 here mean?

A: they represent different coordinate axes: the annotation in the code is rotation_matrix.eulerAngles(2, 1, 0); // ZYX order, namely roll pitch
yaw order. Check the official website of eigen and see the following links Eigen: Geometry module Each of the three parameters a0,a1,a2 is found
represents the respective rotation axis as an integer in {0,1,2}. For instance, in:Vector3f ea = mat.eulerAngles(2, 0, 2); "2" represents the z axis and "0" the x axis, etc.

1. The Euclidean transformation matrix uses T.rotate() in the code. Can you choose another way to rotate it?

A: Yes, the specific types of support also need to be defined here Eigen: Eigen::Transform< _Scalar, _Dim, _Mode, _Op... Can see
To support all our rotation types.

Tip: if you don't understand a function, you can find the definition and read and write more code.

Attachment: calculation method of rotation matrix:

rot(x, θ) Indicates rotation about the X axis θ Indicates the angle of rotation. The same is true for others. The lower right corner of the matrix represents the magnification. The 4th row and 4th column of the matrix can be omitted

reference resources:
Learn SLAM from scratch | rotation of rigid bodies in three-dimensional space