Pytorch:Hollow Convolution Neural Network
Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology
This tutorial is not commercial and is only for learning and reference exchange. If you need to reproduce it, please contact me.
Void convolution adds voids to the convolution core as opposed to ordinary convolution. 0 0 0 element), thereby increasing the field of feeling and getting more information. Reception fields are the area sizes of the input layer corresponding to an element in the output of a layer in a convolution neural network. A common explanation is that a point on the feature map corresponds to the area size on the input graph.
For a 3 × 3 3\times3 3 × 3 2 2 2-Void convolution, the actual convolution kernel size or 3 × 3 3\times3 3 × 3. But the void is 1 1 1, so the convolution kernel expands one 7 × 7 7\times7 7 × 7 image blocks, but only 9 9 Nine red points will have weights to convolute. It can also be understood that the size of the convolution kernel is 7 × 7 7\times7 7 × 7, but only in the diagram 9 9 9 points do not have a weight of 0 0 0, all others are 0 0 0. The actual convolution weight is only 3 × 3 3\times3 3 × 3, but the receptive field is actually 7 × 7 7\times7 7 × 7. about 15 × 15 15\times15 15 × 15, the actual convolution is only 9 × 9 9\times9 9×9 .
At nn. In the Conv2d() function, by adjusting the value of dilation, the void convolution of convolution kernels of different sizes can be performed.
The void convolution network we built has two void convolution layers, two pooling layers and two fully connected layers, and the classifier still contains 10 10 Ten neurons, with the exception of differences in convolution modes, share the same network structure as the one used to identify FashionMNIST.
Construction of Hole Convolution Neural Network
import numpy as np import pandas as pd from sklearn.metrics import accuracy_score, confusion_matrix import matplotlib.pyplot as plt import seaborn as sns import copy import time import torch import torch.nn as nn from torch.optim import Adam import torch.utils.data as Data from torchvision import transforms from torchvision.datasets import FashionMNIST
class MyConvDilaNet(nn.Module):
def __init__(self):
super(MyConvDilaNet, self).__init__()
# Define the first layer of convolution
self.conv1 = nn.Sequential(
nn.Conv2d(
in_channels = 1, # Number of input image channels
out_channels = 16, # Number of Output Features (Number of Convolution Kernels)
kernel_size = 3, # Convolution Kernel Size
stride = 1, # Convolutional Kernel Step 1
padding = 1, # Edge Fill 1
dilation = 2,
),
nn.ReLU(), # Activation function
nn.AvgPool2d(
kernel_size = 2, # Average pooling, 2*2
stride = 2, # Pooling step 2
),
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 32, 3, 1, 0, dilation = 2),
nn.ReLU(),
nn.AvgPool2d(2, 2),
)
self.classifier = nn.Sequential(
nn.Linear(32 * 4 * 4, 256),
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 10),
)
def forward(self, x):
# Define Forward Propagation Path
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0), -1) # Flattening a multidimensional convolution layer
output = self.classifier(x)
return output
Data Preprocessing
The data preprocessing section is the same as above.
# Prepare training datasets using FashionMNIST data
train_data = FashionMNIST(
root = './data/FashionMNIST',
train = True,
transform = transforms.ToTensor(),
download = False
)
# Define a data loader
train_loader = Data.DataLoader(
dataset = train_data, # data set
batch_size = 64, # Size of batch processing
shuffle = False, # Do not clutter data
num_workers = 2, # Two processes
)
# Calculate batch number
print(len(train_loader))
# Get batch data
for step, (b_x, b_y) in enumerate(train_loader):
if step > 0:
break
# Visualize an image of a batch
batch_x = b_x.squeeze().numpy()
batch_y = b_y.numpy()
label = train_data.classes
label[0] = 'T-shirt'
plt.figure(figsize = (12, 5))
for i in np.arange(len(batch_y)):
plt.subplot(4, 16, i + 1)
plt.imshow(batch_x[i, :, :], cmap = plt.cm.gray)
plt.title(label[batch_y[i]], size = 9)
plt.axis('off')
plt.subplots_adjust(wspace = 0.05)
# Processing Test Sets
test_data = FashionMNIST(
root = './data/FashionMNIST',
train = False, # Do not use training datasets
download = False
)
# Add a channel dimension to the data and normalize the range of values
test_data_x = test_data.data.type(torch.FloatTensor) / 255.0
test_data_x = torch.unsqueeze(test_data_x, dim = 1)
test_data_y = test_data.targets # Test Set Label
print(test_data_x.shape)
print(test_data_y.shape)
938 torch.Size([10000, 1, 28, 28]) torch.Size([10000])

# Define hollow network objects myconvdilanet = MyConvDilaNet()
from torchsummary import summary summary(myconvdilanet, input_size=(1, 28, 28))
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 16, 26, 26] 160
ReLU-2 [-1, 16, 26, 26] 0
AvgPool2d-3 [-1, 16, 13, 13] 0
Conv2d-4 [-1, 32, 9, 9] 4,640
ReLU-5 [-1, 32, 9, 9] 0
AvgPool2d-6 [-1, 32, 4, 4] 0
Linear-7 [-1, 256] 131,328
ReLU-8 [-1, 256] 0
Linear-9 [-1, 128] 32,896
ReLU-10 [-1, 128] 0
Linear-11 [-1, 10] 1,290
================================================================
Total params: 170,314
Trainable params: 170,314
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.24
Params size (MB): 0.65
Estimated Total Size (MB): 0.89
----------------------------------------------------------------
# Output Network Structure
from torchviz import make_dot
x = torch.randn(1, 1, 28, 28).requires_grad_(True)
y = myconvdilanet(x)
myDilaCNN_vis = make_dot(y, params=dict(list(myconvdilanet.named_parameters()) + [('x', x)]))
myDilaCNN_vis
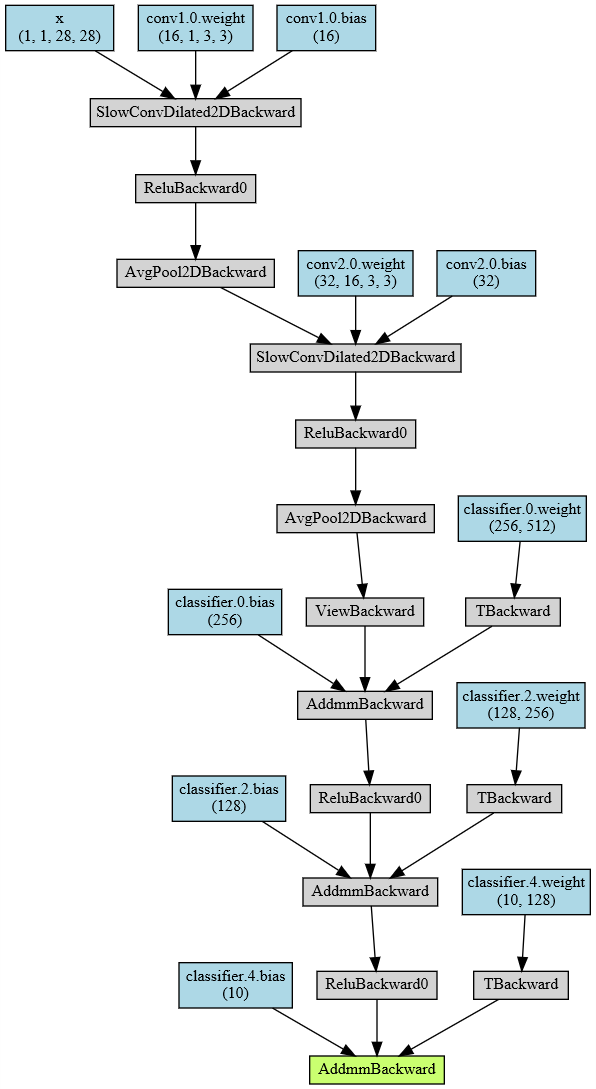
Training and Prediction of Hole Convolution Neural Network
The network training and testing section is the same as above.
# Define network training process functions
def train_model(model, traindataloader, train_rate, criterion, optimizer, num_epochs = 25):
'''
Model, training dataset(To be sliced),Percentage of training set, loss function, optimizer, number of training rounds
'''
# Calculate the number of batch es used for training
batch_num = len(traindataloader)
train_batch_num = round(batch_num * train_rate)
# Copy model parameters
best_model_wts = copy.deepcopy(model.state_dict())
best_acc = 0.0
train_loss_all = []
val_loss_all =[]
train_acc_all = []
val_acc_all = []
since = time.time()
# Training Framework
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch, num_epochs - 1))
print('-' * 10)
train_loss = 0.0
train_corrects = 0
train_num = 0
val_loss = 0.0
val_corrects = 0
val_num = 0
for step, (b_x, b_y) in enumerate(traindataloader):
if step < train_batch_num:
model.train() # Set as training mode
output = model(b_x)
pre_lab = torch.argmax(output, 1)
loss = criterion(output, b_y) # Calculating Error Loss
optimizer.zero_grad() # Empty Past Gradient
loss.backward() # Error Back Propagation
optimizer.step() # Update parameters based on errors
train_loss += loss.item() * b_x.size(0)
train_corrects += torch.sum(pre_lab == b_y.data)
train_num += b_x.size(0)
else:
model.eval() # Set to Verification Mode
output = model(b_x)
pre_lab = torch.argmax(output, 1)
loss = criterion(output, b_y)
val_loss += loss.item() * b_x.size(0)
val_corrects += torch.sum(pre_lab == b_y.data)
val_num += b_x.size(0)
# ==========================End of small loop=======================End of small loop==========
# Calculate loss and accuracy of an epoch on training and validation sets
train_loss_all.append(train_loss / train_num)
train_acc_all.append(train_corrects.double().item() / train_num)
val_loss_all.append(val_loss / val_num)
val_acc_all.append(val_corrects.double().item() / val_num)
print('{} Train Loss: {:.4f} Train Acc: {:.4f}'.format(epoch, train_loss_all[-1], train_acc_all[-1]))
print('{} Val Loss: {:.4f} Val Acc: {:.4f}'.format(epoch, val_loss_all[-1], val_acc_all[-1]))
# Parameters with the highest precision of the copy model
if val_acc_all[-1] > best_acc:
best_acc = val_acc_all[-1]
best_model_wts = copy.deepcopy(model.state_dict())
time_use = time.time() - since
print('Train and Val complete in {:.0f}m {:.0f}s'.format(time_use // 60, time_use % 60))
# ===============================End of Big Loop==========================
# Parameters using the best model
model.load_state_dict(best_model_wts)
train_process = pd.DataFrame(
data = {'epoch': range(num_epochs),
'train_loss_all': train_loss_all,
'val_loss_all': val_loss_all,
'train_acc_all': train_acc_all,
'val_acc_all': val_acc_all})
return model, train_process
# Training the model optimizer = Adam(myconvdilanet.parameters(), lr = 0.0003) criterion = nn.CrossEntropyLoss() myconvdilanet, train_process = train_model(myconvdilanet, train_loader, 0.8, criterion, optimizer, num_epochs = 25)
Epoch 0/24 ---------- 0 Train Loss: 0.8922 Train Acc: 0.6718 0 Val Loss: 0.6322 Val Acc: 0.7498 Train and Val complete in 1m 2s Epoch 1/24 ---------- 1 Train Loss: 0.6028 Train Acc: 0.7656 1 Val Loss: 0.5610 Val Acc: 0.7837 Train and Val complete in 2m 3s Epoch 2/24 ---------- 2 Train Loss: 0.5331 Train Acc: 0.7948 2 Val Loss: 0.5047 Val Acc: 0.8107 Train and Val complete in 3m 3s Epoch 3/24 ---------- 3 Train Loss: 0.4868 Train Acc: 0.8159 3 Val Loss: 0.4738 Val Acc: 0.8266 Train and Val complete in 3m 60s Epoch 4/24 ---------- 4 Train Loss: 0.4540 Train Acc: 0.8320 4 Val Loss: 0.4491 Val Acc: 0.8369 Train and Val complete in 4m 54s Epoch 5/24 ---------- 5 Train Loss: 0.4275 Train Acc: 0.8433 5 Val Loss: 0.4279 Val Acc: 0.8455 Train and Val complete in 5m 50s Epoch 6/24 ---------- 6 Train Loss: 0.4047 Train Acc: 0.8512 6 Val Loss: 0.4075 Val Acc: 0.8531 Train and Val complete in 6m 45s Epoch 7/24 ---------- 7 Train Loss: 0.3851 Train Acc: 0.8591 7 Val Loss: 0.3897 Val Acc: 0.8608 Train and Val complete in 7m 41s Epoch 8/24 ---------- 8 Train Loss: 0.3690 Train Acc: 0.8655 8 Val Loss: 0.3762 Val Acc: 0.8653 Train and Val complete in 8m 36s Epoch 9/24 ---------- 9 Train Loss: 0.3557 Train Acc: 0.8708 9 Val Loss: 0.3652 Val Acc: 0.8672 Train and Val complete in 9m 31s Epoch 10/24 ---------- 10 Train Loss: 0.3440 Train Acc: 0.8751 10 Val Loss: 0.3552 Val Acc: 0.8710 Train and Val complete in 10m 26s Epoch 11/24 ---------- 11 Train Loss: 0.3341 Train Acc: 0.8776 11 Val Loss: 0.3473 Val Acc: 0.8735 Train and Val complete in 11m 22s Epoch 12/24 ---------- 12 Train Loss: 0.3250 Train Acc: 0.8812 12 Val Loss: 0.3412 Val Acc: 0.8762 Train and Val complete in 12m 21s Epoch 13/24 ---------- 13 Train Loss: 0.3166 Train Acc: 0.8840 13 Val Loss: 0.3355 Val Acc: 0.8791 Train and Val complete in 13m 25s Epoch 14/24 ---------- 14 Train Loss: 0.3092 Train Acc: 0.8870 14 Val Loss: 0.3299 Val Acc: 0.8810 Train and Val complete in 14m 26s Epoch 15/24 ---------- 15 Train Loss: 0.3023 Train Acc: 0.8889 15 Val Loss: 0.3250 Val Acc: 0.8816 Train and Val complete in 15m 28s Epoch 16/24 ---------- 16 Train Loss: 0.2956 Train Acc: 0.8921 16 Val Loss: 0.3182 Val Acc: 0.8838 Train and Val complete in 16m 30s Epoch 17/24 ---------- 17 Train Loss: 0.2896 Train Acc: 0.8939 17 Val Loss: 0.3138 Val Acc: 0.8862 Train and Val complete in 17m 32s Epoch 18/24 ---------- 18 Train Loss: 0.2836 Train Acc: 0.8961 18 Val Loss: 0.3093 Val Acc: 0.8872 Train and Val complete in 18m 33s Epoch 19/24 ---------- 19 Train Loss: 0.2783 Train Acc: 0.8984 19 Val Loss: 0.3054 Val Acc: 0.8894 Train and Val complete in 19m 34s Epoch 20/24 ---------- 20 Train Loss: 0.2728 Train Acc: 0.9004 20 Val Loss: 0.3020 Val Acc: 0.8911 Train and Val complete in 20m 52s Epoch 21/24 ---------- 21 Train Loss: 0.2676 Train Acc: 0.9021 21 Val Loss: 0.2989 Val Acc: 0.8922 Train and Val complete in 21m 54s Epoch 22/24 ---------- 22 Train Loss: 0.2625 Train Acc: 0.9038 22 Val Loss: 0.2960 Val Acc: 0.8942 Train and Val complete in 22m 55s Epoch 23/24 ---------- 23 Train Loss: 0.2578 Train Acc: 0.9049 23 Val Loss: 0.2932 Val Acc: 0.8942 Train and Val complete in 23m 56s Epoch 24/24 ---------- 24 Train Loss: 0.2531 Train Acc: 0.9062 24 Val Loss: 0.2907 Val Acc: 0.8942 Train and Val complete in 24m 58s
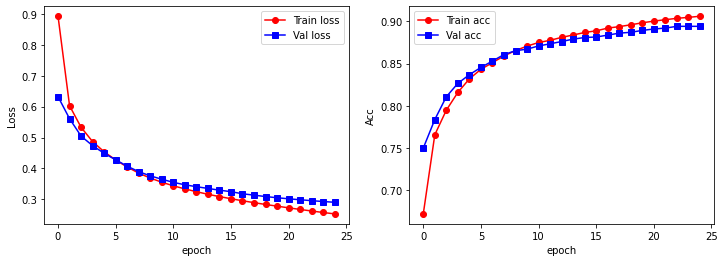
Visualize the training process using line charts:
# Visual training process
plt.figure(figsize = (12, 4))
plt.subplot(1, 2, 1)
plt.plot(train_process.epoch, train_process.train_loss_all, 'ro-', label = 'Train loss')
plt.plot(train_process.epoch, train_process.val_loss_all, 'bs-', label = 'Val loss')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('Loss')
plt.subplot(1, 2, 2)
plt.plot(train_process.epoch, train_process.train_acc_all, 'ro-', label = 'Train acc')
plt.plot(train_process.epoch, train_process.val_acc_all, 'bs-', label = 'Val acc')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('Acc')
plt.show()
Compute the generalization ability of the void convolution model:
# Test Set Prediction and Visualize Prediction Effect
myconvdilanet.eval()
output = myconvdilanet(test_data_x)
pre_lab = torch.argmax(output, 1)
acc = accuracy_score(test_data_y, pre_lab)
print(test_data_y)
print(pre_lab)
print('The prediction accuracy on the test set is', acc)
tensor([9, 2, 1, ..., 8, 1, 5]) tensor([9, 2, 1, ..., 8, 1, 5]) Prediction accuracy on test set is 0.8841
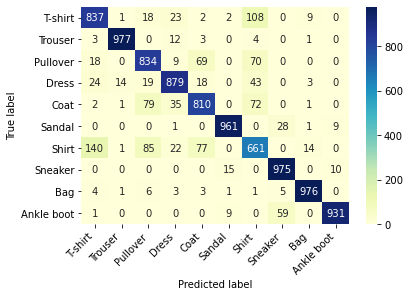
Using thermograms, observe the predictions on each type of data:
# Compute and visualize confusion matrices on test sets
conf_mat = confusion_matrix(test_data_y, pre_lab)
df_cm = pd.DataFrame(conf_mat, index = label, columns = label)
heatmap = sns.heatmap(df_cm, annot = True, fmt = 'd', cmap = 'YlGnBu')
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation = 0, ha = 'right')
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation = 45, ha = 'right')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()