Realization of n-order Bessel Curve Formula
If you don't know what Bessel Curve is and what it can be used for, you can go to the following article first. Bessel Curve Literacy
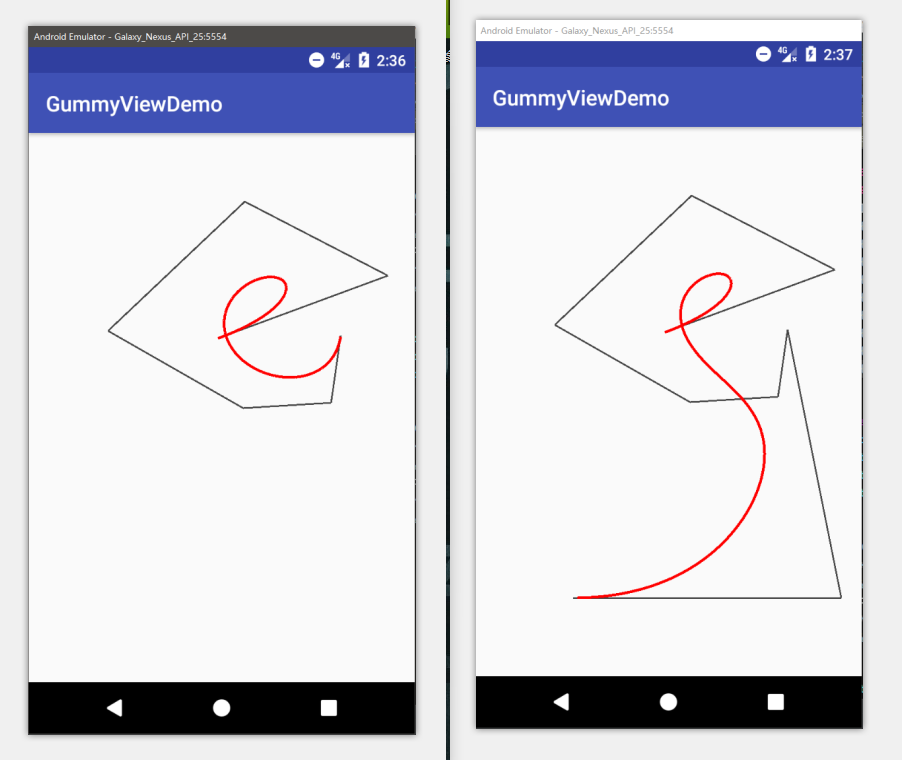
1. Effect Reference
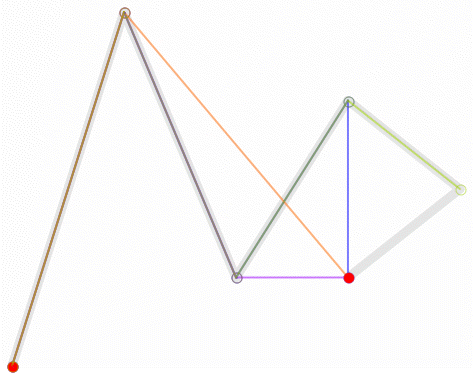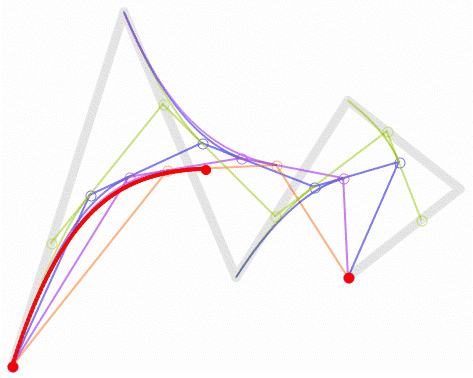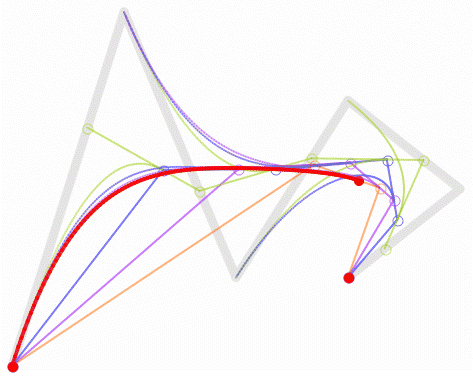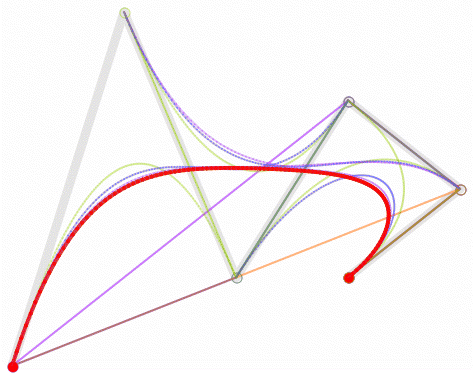
|

|
2. Idea analysis
The general parameter formula given in Baidu Encyclopedia is as follows:
Given point P 0, P 1, P 2,... Pn, its Bessel curve formula is as follows (that is, point B(t) on the Bessel curve can be calculated by the following formula): 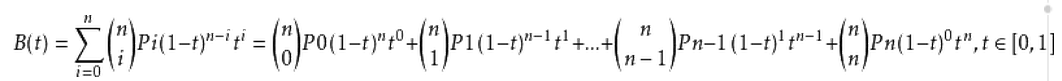
It can be seen that the formula is expressed by the sum of a fixed-form expression, which is the key: 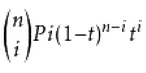
The expression can be divided into four parts:
- The Constant Part Increasing from i to n
- Pi coordinate part
- (1 - t)^(n - i)
- t^i
It can be seen that these four parts are all related to the value of I. In addition, the calculation of t value is as follows: i/(n+1)
If it is abstract to find rules directly from the above formulas, then find rules from concrete examples.
Let Bt be the coordinates on the Bessel curve to be calculated, N be the number of control points, P 0, P 1, P 2... P n be the coordinates of the control points on the Bessel curve. When N is different, there are the following calculation formulas:
If N is 3, there are three control points of Bessel curve, then n is 2. These three points are expressed by P 0, P 1 and P 2 respectively.
- N = 3: P = (1-t)^2*P0 + 2*(1-t)*t*P1 + t^2*P2
- N = 4: P = (1-t)^3*P0 + 3*(1-t)^2*t*P1 + 3(1-t)*t^2*P2 + t^3*P3
- N = 5: P = (1-t)^4*P0 + 4*(1-t)^3*t*P1 + 6(1-t)^2*t^2*P2 + 4*(1-t)*t^3*P3 + t^4*P4
The expression of general parameter formula of Bessel curve is expressed as follows:
With constants a,b and c, the expression can be expressed as follows:
a * (1 - t)^b * t^c * Pn;
The corresponding values of a, B and C are analyzed when N is 3, 4 and 5 respectively.
For example, when N = 3, the formula has three expressions. The first expression is (1-t) ^ 2*P 0, which corresponds to the values of a, B and c: 1, 2, 0, respectively.
- N = 3: 1,2,0 2,1,1 1,0,2
a: 1 2 1
b: 2 1 0
c: 0 1 2 - N = 4: 1,3,0 3,2,1 3,1,2 1,0,3
a: 1 3 3 1
b: 3 2 1 0
c: 0 1 2 3 - N = 5: 1,4,0 4,3,1 6,2,2 4,1,3 1,0,4
a: 1 4 6 4 1
b: 4 3 2 1 0
c: 0 1 2 3 4
Based on the above analysis, we can summarize the rules of value selection for a, B and C.
- b: (N - 1) decreases to 0 (b is a power of 1-t)
- c: 0 increments to (N - 1) (c is the power of t)
- a: When N is 1, 2, 3, 4, 5 respectively, its value is expressed as follows:
N=1:-—1
N=2:-–1 1
N=3:-1 2 1
N=4:—–1 3 3 1
N=5:—1 4 6 4 1
The rule for changing a value is as follows: Yang Hui Triangle
3. Implement it in java
Now let's implement it: let's start with another example
For example, the coordinates of control points are calculated as follows: P 0 (3,8), P 1 (2,3), P 2 (2,7). If you want to return 10 points on the Bessel curve, you can write in java as follows:
float[] p0 = {3, 8};
float[] p1 = {4, 3};
float[] p2 = {2, 7};
float[][] result = new float[10][2];
for (int i = 0; i < 10; i++) {
float t = i / 10;
result[i][0] = (float) (1 * Math.pow(1 - t, 2) * Math.pow(t, 0) * p0[0] + 2 * Math.pow(1 - t, 1) * Math.pow(t, 1) * p1[0] + 1 * Math.pow(1 - t, 0) * Math.pow(t, 2) * p2[0]);
result[i][1] = (float) (1 * Math.pow(1 - t, 2) * Math.pow(t, 0) * p0[1] + 2 * Math.pow(1 - t, 1) * Math.pow(t, 1) * p1[1] + 1 * Math.pow(1 - t, 0) * Math.pow(t, 2) * p2[1]);
}Well, the final calculation method is the following:
/**
* @param poss Coordinates of control points of Bessel curve
* @param precision Accuracy, the number of points on the Bessel curve that need to be calculated
* @return Points on this Bessel curve (two-dimensional coordinates)
*/
public float[][] calculate(float[][] poss, int precision) {
//Dimension, number of coordinate axes (two-dimensional coordinates, three-dimensional coordinates...)
int dimersion = poss[0].length;
//Bessel Curve Control Points (Order)
int number = poss.length;
//Control points not less than 2, at least in two-dimensional coordinate system
if (number < 2 || dimersion < 2)
return null;
float[][] result = new float[precision][dimersion];
//Calculating Yang Hui Triangle
int[] mi = new int[number];
mi[0] = mi[1] = 1;
for (int i = 3; i <= number; i++) {
int[] t = new int[i - 1];
for (int j = 0; j < t.length; j++) {
t[j] = mi[j];
}
mi[0] = mi[i - 1] = 1;
for (int j = 0; j < i - 2; j++) {
mi[j + 1] = t[j] + t[j + 1];
}
}
//Computing coordinate points
for (int i = 0; i < precision; i++) {
float t = (float) i / precision;
for (int j = 0; j < dimersion; j++) {
float temp = 0.0f;
for (int k = 0; k < number; k++) {
temp += Math.pow(1 - t, number - k - 1) * poss[k][j] * Math.pow(t, k) * mi[k];
}
result[i][j] = temp;
}
}
return result;
}Inheriting View in android and rewriting onDraw method, adding the custom View in the Activity-bound layout file, calling the calculate method can draw any order of Bessel curve.
........
// Implementation of calculate method in BezierImpl
private BezierImpl bezier = new BezierImpl();
private Paint paint = new Paint();
float[][] poss = {
{353.0f, 383.0f},
{670.0f, 266.0f},
{403.0f, 128.0f},
{148.0f, 369.0f},
{400.0f, 513.0f},
{564.0f, 503.0f},
{582.0f, 378.0f},
{682.0f, 878.0f},
{182.0f, 878.0f}
};
@Override
protected void onDraw(Canvas canvas) {
float x0, y0, x, y;
paint.setColor(Color.DKGRAY);
paint.setStrokeWidth(3.0f);
x0 = poss[0][0];
y0 = poss[0][1];
for (int i = 1; i < poss.length; i++) {
x = poss[i][0];
y = poss[i][1];
canvas.drawLine(x0, y0, x, y, paint);
x0 = x;
y0 = y;
}
paint.setColor(Color.RED);
paint.setStrokeWidth(5.0f);
float[][] po = bezier.calculate(poss, 500);
x0 = po[0][0];
y0 = po[0][1];
for (int i = 1; i < 500; i++) {
x = po[i][0];
y = po[i][1];
canvas.drawLine(x0, y0, x, y, paint);
x0 = x;
y0 = y;
}
}
...........Finally, a custom View (GummyView) is posted, which uses the Bessel curve and the above method. If you are interested, you can leave a message for me or Fork.
Address: DuanJiaNing/GummyView
The effect achieved at present is as follows:
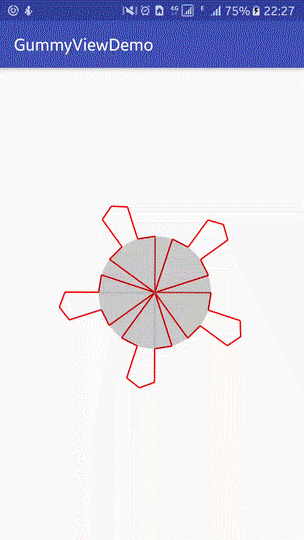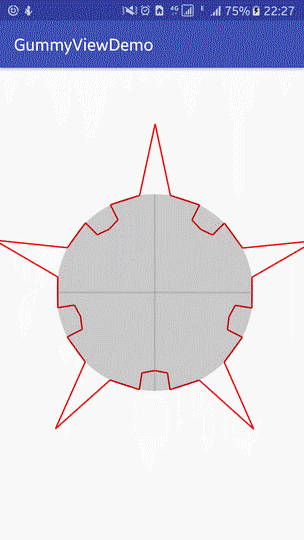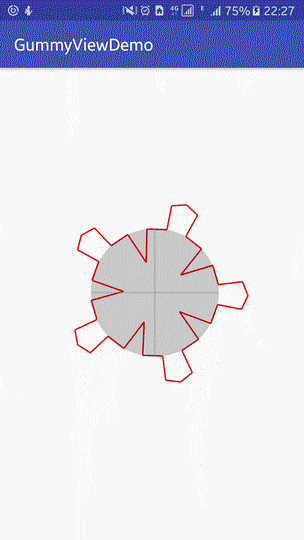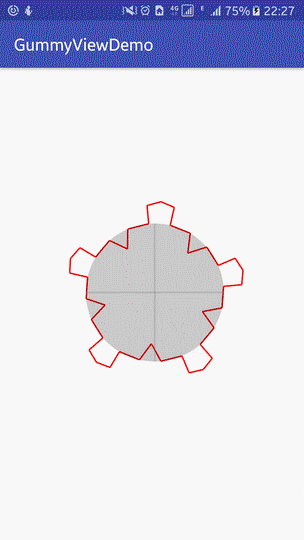 |
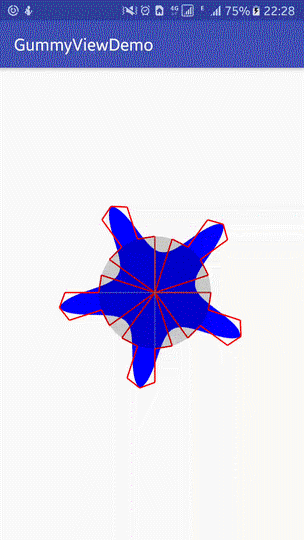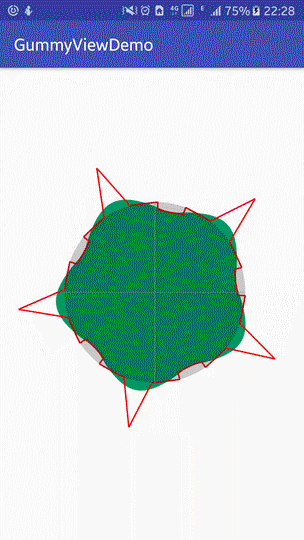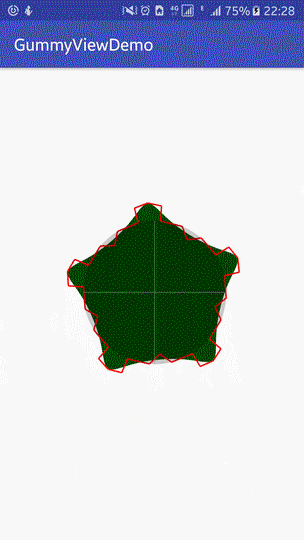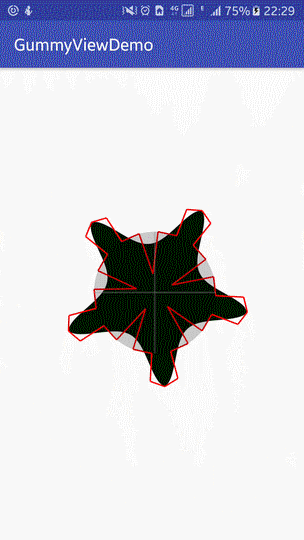 |
 |