Reference Blog: https://blog.csdn.net/qq_34374664/article/details/70149223

 

1. Convex hull

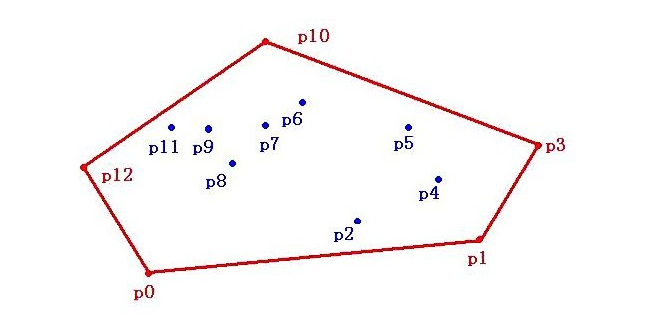
Definition: Suppose that there are several points on the plane, through which a polygon can be made, so that the polygon can "wrap up" all the points. When this polygon is a convex polygon, we call it a "convex hull".

Solution: I only have Graham scanning at present, but I think it's enough.

Steps:

If all points are placed in the two-dimensional coordinate system, the point with the smallest ordinate must be the point on the convex hull, as shown in figure P 0.
2. Shift all the coordinates so that P0 is the origin, as shown above.
3. Calculate the angle alpha of each point relative to P0, and rank each point in order from small to large. When alpha is the same, the nearest to P0 is in the front. For example, the results of the above figure are P1, P2, P3, P4, P5, P6, P7, P8. We can know from geometric knowledge that the first point P1 and the last point P8 in the result must be points on the convex hull.
(Above is the preparatory step, and the convex hull is found below.)
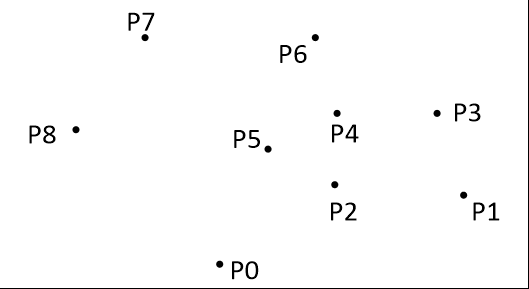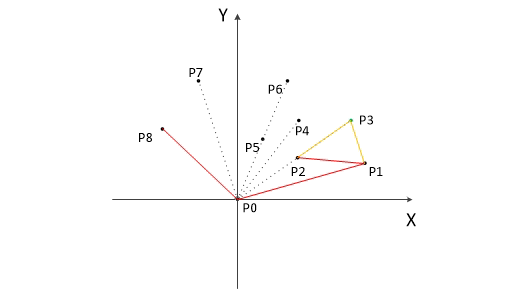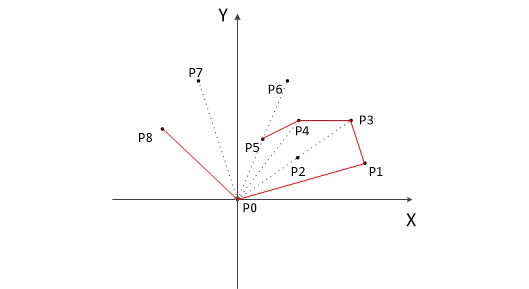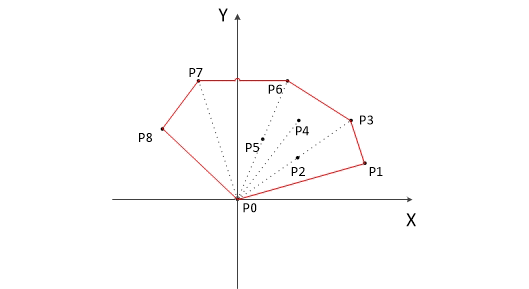
Above all, we already know the first point P0 and the second point P1 on the convex hull, and we put them in the stack. Now from the result obtained in step 3, take the point behind P1 as the current point, that is, P2. Next, start looking for a third point:
4. Connect P0 with the point at the top of the stack to get the straight line L. See if the current point is on the right or left side of the line L. If it is on the right side of the line, step 5 is executed; if it is on the line, or on the left side of the line, step 6 is executed.
5. If on the right, the top element of the stack is not a point on the convex hull, and the top element of the stack is put out of the stack. Step 4.
6. The current point is the point on the convex hull. Push it on the stack and execute step 7.
7. Check whether the current point P2 is the last element of the result in Step 3. If it's the last element, it's over. If not, make the point behind P2 the current point and return to step 4.

Finally, the elements in the stack are the points on the convex hull.
The following is the process of dynamic solution using Graham scanning method:

I understand the steps:

1. Find the lowest left-hand point p

2. Regarding p as the origin, the relative polar angle is sorted if the polar angle is close to the same distance.

3. Put the first two points on the stack, and each additional point determines whether or not the stack is turned left or not.

Code (POJ3335):

//Find the distance between two points 
double dis(Point a,Point b)
{
	return sqrt((a-b)*(a-b));
}
//Sort by polar angle with c[0] as origin 
bool cmp(const Point& a,const Point& b)
{
	x=(a-c[0])^(b-c[0]);
	if(sgn(x)==0)
	{
		return dis(c[0],a)<dis(c[0],b);
	}
	else if(x>0) return 1;
	else return 0;
}
//When finding convex hulls, judge whether to turn left, including collinear points 
bool check(Point a,Point b,Point c)
{
	x=(b-a)^(c-a); 
	return sgn(x)<0;
}
//Sort points counter-clockwise 
void sort_point(Point *p,int n)
{
	pos=0;		
	for(int i=0;i<n;i++)
		if(p[i].y<p[pos].y || (p[i].y==p[pos].y&&p[i].x<p[pos].x))
			pos=i;
	swap(p[0],p[pos]);
	for(int i=0;i<n;i++)
		c[i]=p[i];
	sort(c+1,c+n,cmp);
	for(int i=0;i<n;i++)
		p[i]=c[i];	
}
//Finding convex hull 
void getconv(Point *p,int& n)
{
	st[0]=p[0];
	st[1]=p[1];
	top=1;
	for(int i=2;i<n;i++)
	{
		//Must turn left 
		while(top>1&&check(st[top-1],st[top],p[i])) 
			top--;			
		st[++top]=p[i];
	}
	n=top;		
}

2. Rotary chuck

Pre-concept:

Heel pair: The point pair farthest from each other on the convex hull.

Understanding: Rotating chuck is exactly an algorithm on convex hull (convex polygon). The chuck is to find a pair of heel points and then make parallel lines, so that the convex polygon is stuck. Then, rotate the pair of parallel lines together until a line and edge coincide. Because the area size of the point and edge and the heel pair change counterclockwise, we can quickly find all pairs of heels, and then find some pairs of points such as the nearest/far point on the plane, the length/width of the convex hull and so on.

Code (POJ3608):

double dis(Point a,Point b)
{
	return sqrt((a-b)*(a-b));
}
bool cmp(const Point& a,const Point& b)
{
	x=(a-c[0])^(b-c[0]);
	if(sgn(x)==0)
	{
		return dis(c[0],a)<dis(c[0],b);
	}
	else if(x>0) return 1;
	else return 0;
}
//On segment L, the nearest point to P 
Point NearestPointToLineSeg(Point P,Line L)
{
    Point result;
    double t = ((P-L.s)*(L.e-L.s))/((L.e-L.s)*(L.e-L.s));
    if(t >= 0 && t <= 1)
    {
        result.x = L.s.x + (L.e.x - L.s.x)*t;
        result.y = L.s.y + (L.e.y - L.s.y)*t;
    }
    else
    {
        if(dis(P,L.s) < dis(P,L.e))
            result = L.s;
        else result = L.e;
    }
    return result;
}
//Distance from point p0 to line segment p1p2
double pointtoseg(Point p0,Point p1,Point p2)
{
    return dis(p0,NearestPointToLineSeg(p0,Line(p1,p2)));
}
//Distance between parallel segments p0p1 and p2p3
double dispallseg(Point p0,Point p1,Point p2,Point p3)
{
    double ans1 = min(pointtoseg(p0,p2,p3),pointtoseg(p1,p2,p3));
    double ans2 = min(pointtoseg(p2,p0,p1),pointtoseg(p3,p0,p1));
    return min(ans1,ans2);
}
//The position relations of vectors a1a2 and b1b2 are obtained.
double Get_angle(Point a1,Point a2,Point b1,Point b2)
{
    Point t = b1 - ( b2 - a1 );
    return (a2-a1)^(t-a1);
} 
//Comparisons in finding convex hulls 
bool check(Point a,Point b,Point c)
{
	x=(b-a)^(c-a);
	return sgn(x)<=0;
}
//Sort points counter-clockwise 
void sort_point(Point *p,int n)
{
		pos=0;		
		for(int i=0;i<n;i++)
		{
			scanf("%lf%lf",&p[i].x,&p[i].y);
			if(p[i].y<p[pos].y || (p[i].y==p[pos].y&&p[i].x<p[pos].x))
				pos=i;
		}
		swap(p[0],p[pos]);
		for(int i=0;i<n;i++)
			c[i]=p[i];
		sort(c+1,c+n,cmp);
		for(int i=0;i<n;i++)
			p[i]=c[i];	
}
//Finding convex hull 
void getconv(Point *p,int& n)
{
	st[0]=p[0];
	st[1]=p[1];
	top=1;
	for(int i=2;i<n;i++)
	{
		//Counterclockwise must turn left 
		while(top>1&&check(st[top-1],st[top],p[i])) 
			top--;			
		st[++top]=p[i];
	}	
	n=top+1;
	for(int i=0;i<n;i++)
		p[i]=st[i];
}
double getarea(Point a,Point b,Point c)
{
	return (a-c)^(b-c);	
}

//Rotating chuck to find the closest distance between two convex hulls
//Enumerate the edges of a convex hull to find the farthest point in another convex hull 
double rc(Point *p,int np,Point *q,int nq)
{

	double ans=1e40,tmp;
	int pp=0,qq=0,temp;
	//ymin is 0
	//Find ymax 
	for(int i=0;i<nq;i++)
		if(sgn(q[i].y-q[qq].y)>0)
			qq=i;
	for(int i=0;i<np;i++)
	{
         //Both ways of writing depend on whether distance can get farther or not. 
		//while(sgn(tmp = get_angle(p[pp],p[(pp+1)%np],q[qq],q[(qq+1)%nq])) < 0 )
        while(sgn(tmp = getarea(p[pp],p[(pp+1)%np],q[qq])-getarea(p[pp],p[(pp+1)%np],q[(qq+1)%nq]))<0) 
		    qq = (qq + 1)%nq;
        //The distance between a point and a line segment cannot be calculated directly because the nearest point may not be on the line segment.
		//That is, when the crossing point is used as the vertical line, the vertical foot is not on the line segment.    
        if(sgn(tmp) == 0)
            ans = min(ans,dispallseg(p[pp],p[(pp+1)%np],q[qq],q[(qq+1)%nq]));
        else ans = min(ans,pointtoseg(q[qq],p[pp],p[(pp+1)%np]));
		pp=(pp+1)%np;
	}
	return ans;
}