Target Reflected Echo Detection Algorithms and Their Implementation on FPGA Part 3:
Top-level Implementation of Square and Integral Circuits and Algorithms
Some time ago, I came into contact with a project of sonar target echo detection. The core function of sonar receiver is to recognize the echo of the excitation signal emitted by the transmitter in the reflected echo which contains a lot of noise. I will share the development process and code of this echo recognition algorithm based on FPGA in several articles. Welcome your comments. The following original content is welcomed to be reproduced by netizens, but please indicate the source: https://www.cnblogs.com/helesheng.
In the first part of this series of blogs, based on the simulation results, I believe that the method of calculating target distance by using the results of "cross correlation of reflected echo and excitation signal" has high performance and computational efficiency. In the second blog post in this series, I implemented data cross-correlation/convolution/FIR filter calculation using a semi-parallel "dual-memory convolution section" structure in the low-cost FPGA of Cyclone series. As the third blog article in this series, I will implement the square sum integral calculation of cross-correlation signals, and combine all the algorithms in the top-level file as a whole.
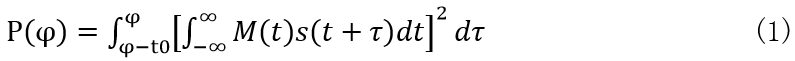
By looking for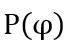 
The location of the extreme point of the target reflector is used to determine the time point when the target reflects the echo.
In Formula (1)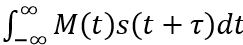
It is the part of cross-correlation algorithm, and its implementation on FPGA has been introduced in the previous paper. According to the symbols defined above, the discretized cross-correlation signal is recorded as R[k]. After further discretization, (1) can be rewritten to the following form that can be implemented by FPGA:
1. Realization of Square Circuit
Using MegaWizard in Quartus-II to configure the square computing circuit, the structure is shown in the following figure.
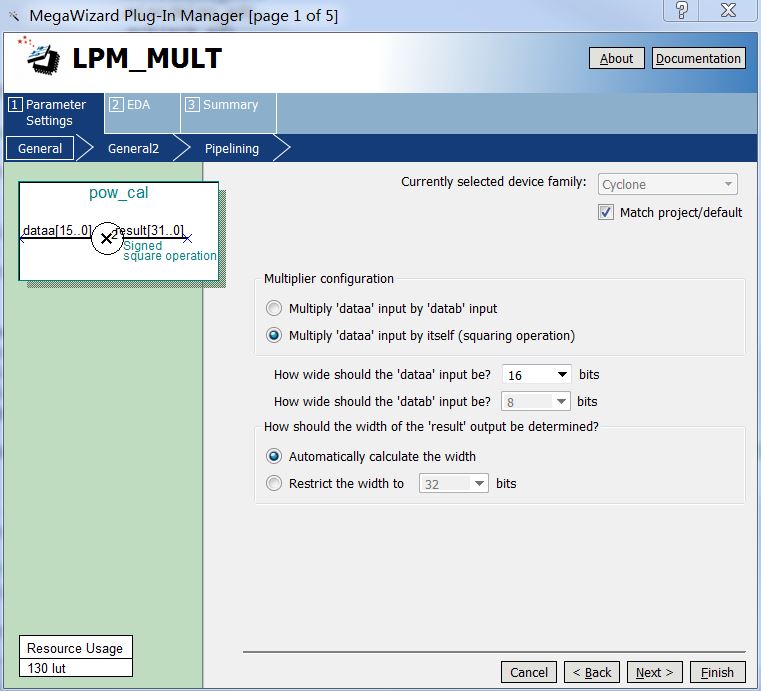
Figure 1 Square Circuit Configuration
II. Design of Integral Circuit
According to formula (2), in order to calculate the value of objective function P[n], it is necessary to sum (integrate) the historical values. Of course, we can use buffers to store historical k0 values and sum the k0 values in the buffers before each output. If k0 is equal to the length of the excitation signal N, then N-1 addition must be calculated before each output P[n]. When N is 64 (as mentioned earlier), this is almost an impossible task. I designed the circuit structure shown in the following figure to achieve the summation of 64 historical data.
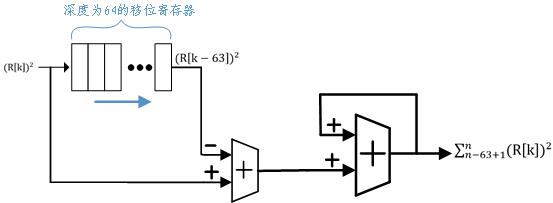
Figure 2 Integrator Circuit Structure
One of the 64-depth shift registers serves to provide "historical data" before 64 samples. First, the current data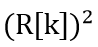
And the oldest historical data
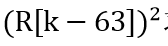Find the difference (complement), and then sum the difference continuously. In this way, according to the law of addition and exchange, the final summation result is equivalent to adding the current data, subtracting the oldest historical data. As long as the initial value of the shift register is all 0, after 64 operations, the sum (integral) of 64 historical data is obtained from the output. The shift register configuration with MegaWizard is shown in the following figure.
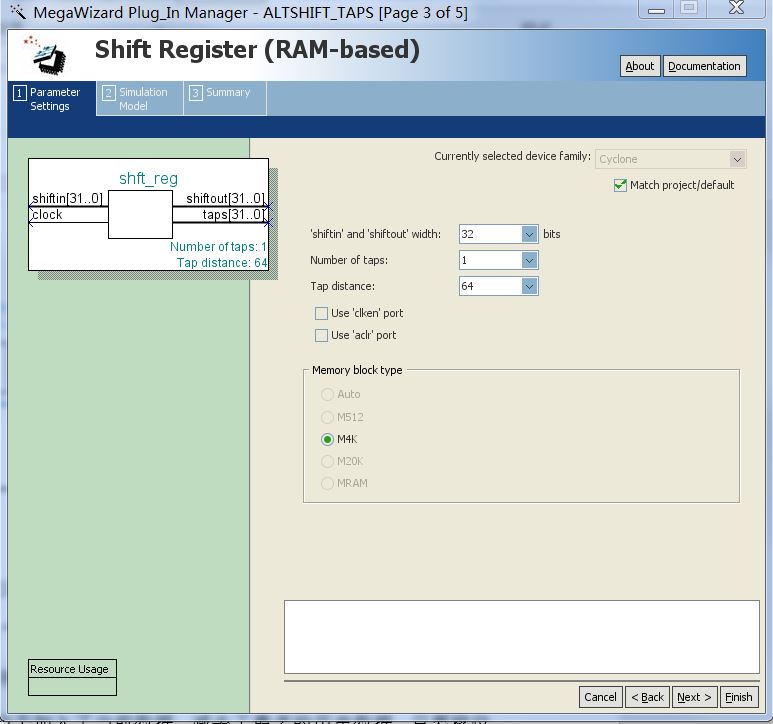
Figure 3 Structure of shift register
The structure of the former subtractor is shown in the following figure.
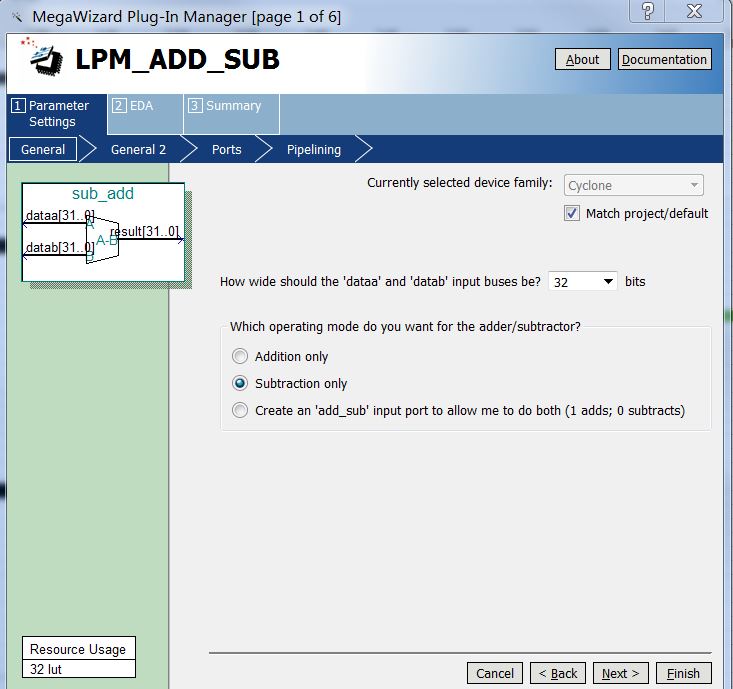
Figure 4 Structure of subtractor
The accumulator is implemented in hardware description language with the following code.
1 always @ (posedge start or negedge rst_n) 2 begin 3 if(!rst_n) 4 acc_out[39:0] <= 40'd0; 5 else begin 6 acc_out[39:0] = $signed(acc_out[39:0]) + $signed(acc_in[31:0]); 7 end 8 end
The keyword $signed denotes an adder with signed numbers.
3. Top-level design of algorithm
In order to connect the aforementioned A/D and D/A control circuit, cross-correlation/convolution/FIR filter circuit and square-sum integral circuit into one system, it is necessary to exemplify and connect the above module circuits in the top-level design documents. In addition, the top-level design document will also control the overall working schedule of the system. The top-level file I designed is shown below.
1 module CONV_POW_AD_DA( 2 ///////////Top-level module, responsible for calling ADC to collect data, convolute, and then output the results of convolution/FIR with DAC///////// 3 input rst_n,//Low level reset signal 4 input iclk20,//External crystal input 20 MHz 5 output sck_da,//D/A Converter SPI Clock 6 output mosi_da,//D/A Converter SPI data signal 7 output cs_da,//D/A Chip Selection Signal of Converter 8 output ld_da,//D/A Dual Channel Data Loading Signal of Converter 9 output sck_ad,//A/D Converter SPI Clock 10 output mosi_ad,//A/D Converter SPI data output 11 input miso_ad,////A/D Converter SPI data input 12 output cs_ad//A/D Converter SPI Mouth Selection Signal 13 ); 14 wire clk; 15 reg start; 16 reg[15:0] cnt;//A timer used to generate the overall cycle 17 reg[11:0] tst_data;//Counter for generating test data 18 parameter CNT_NUM = 16'd2000;//At 100M clock, 2000 frequency division means 50KHz overflow rate 19 wire[11:0] ad_data;//AD Internal connection of conversion results 20 wire[11:0] data_cha;//A Channel data 21 wire[11:0] data_chb;//B Channel data 22 wire[15:0] shft_data1;//Data passed between two sections of convolution 23 wire[15:0] shft_data2;//Data passed between two sections of convolution 24 wire[15:0] shft_data3;//Data passed between two sections of convolution 25 wire[15:0] shft_data4;//Data passed between two sections of convolution 26 wire[39:0] conv_res1;//The results of convolution in Section I 27 wire[39:0] conv_res2;//CONVOLUTION RESULTS IN SECTION 2 28 wire[39:0] conv_res3;//CONVOLUTION RESULTS IN SECTION 3 29 wire[39:0] conv_res4;//CONVOLUTION RESULTS IN SECTION 4 30 wire[39:0] conv_res;//The result of total convolution 31 wire[33:0] acc_sum;//Finally, the cumulative sum of each section is calculated. 32 wire[31:0] shiftout;//Removal data from shift registers 33 wire[15:0] ac_sig;//AC signal after removal of DC bias 34 wire[31:0] pow_sig;//Energy of signal 35 wire signed[31:0] acc_in;//The input of a summation accumulator is also an addition./Output of subtractor 36 reg signed[39:0] acc_out;//The output of the accumulator 37 wire signed[19:0] data_out;//Output of Cumulative Results after Cumulative Formulation 38 39 //assign data_cha[11:0] = acc_out[25:14];//passageway a Output 64 Point Energy Accumulation Results 40 //assign data_cha[11:0] = shiftout[18:7];//passageway a Output data 41 assign data_cha[11:0] = pow_sig[19:8];//passageway a Square of output AC signal 42 //assign data_cha[11:0] = ad_data[11:0];//passageway a Output data 43 //assign data_cha[11:0] = shft_data2[11:0];//passageway a Output data 44 //assign data_chb[11:0] = conv_res[26:15];//passageway b Output data 45 //The coefficient itself is 16. bit Symbolic, as FIR If the sum of the coefficients of the filter is 1, then 16 bits The sum of all the signed coefficients is 32768. 46 //Therefore, it is necessary to shift the filtering result to the right by 15. bit，So take 26 of the results.:15. But because of DA Reference voltage 2.048V，less than AD 3.3V So the filtering result is still slightly smaller. 47 //assign data_chb[11:0] = data_out[14:3];//passageway b Output cumulative result prescription 48 assign data_chb[11:0] = acc_out[28:17];//passageway b Output 64 Point Energy Accumulation Results 49 //assign data_chb[11:0] = pow_sig[20:9];//passageway b Square of output AC signal 50 //assign data_chb[11:0] = acc_sum[26:15];//passageway b Output filtering/Convolution results 51 //assign data_chb[11:0] = conv_res1[26:15];//passageway b Output data 52 53 /////Connections used in the following coefficient configurations///// 54 wire rdy_work;//Configuration Completion Signal, High Level Indicates Configuration Completion 55 wire[7:0] wr_blk_addr;//Backward Coefficient blk Configured address 56 wire[15:0] data_bank;//Directional coefficients blk Configured data 57 wire csh0,csh1,csh2,csh3;//Coefficient allocated for each section blk Gating line 58 PLL20_100 i_pll20_100(//Instantiation PLL Clock generation 59 .inclk0(iclk20), 60 .c0(clk)//pll Output 100 M Working clock 61 ); 62 63 always @ (posedge clk or negedge rdy_work) 64 begin 65 if(!rdy_work) 66 begin 67 start <= 1'd0; 68 cnt[15:0] <= 16'd0; 69 tst_data[11:0] <= 12'd0; //Counters for testing 70 end 71 else begin 72 //////////Maintenance Period Counter/////////// 73 if(cnt < CNT_NUM-1) begin 74 cnt[15:0] <= cnt[15:0] + 16'd1; 75 tst_data[11:0] <= tst_data[11:0]; 76 end 77 else begin 78 cnt[15:0] <= 16'd0; 79 tst_data[11:0] <= tst_data[11:0] + 12'd1; //Counters for testing 80 end 81 82 ////////Generate startup signal///// 83 if((cnt > 102)&(cnt <= 105))//In 105th clk Generate startup signal 84 start <= 1'D1;//Start MCP4822 Output State Machine 85 else 86 start <= 1'D0; 87 end 88 end 89 90 init_coe_blk i_init_coe_blk(//The instantiation coefficient configuration module reads the coefficients from the coefficient pool and directs them to the coefficients. blk The function of configuring data is only valid at the beginning of reset. ready Signal Control Subsequent Module 91 .clk(clk), 92 .rst_n(rst_n),//Overall reset signal 93 .ready(rdy_work),//Configuration Completion Signal, High Level Indicates Configuration Completion 94 .wr_blk_addr(wr_blk_addr),//Backward Coefficient blk Configured address 95 .data_bank(data_bank),//Directional coefficients blk Configured data 96 .csh0(csh0),//Section I Coefficient of Allocation blk Gating line 97 .csh1(csh1),//Section II Coefficient of Allocation blk Gating line 98 .csh2(csh2),//Section 3 Coefficient of Allocation blk Gating line 99 .csh3(csh3)//Section IV Coefficient of Allocation blk Gating line 100 ); 101 102 CONV_SER16 i_conv_ser16_I(//Instantiate the first 16-order convolution/fir Circuit 103 .clk(clk), 104 .a({4'd0,ad_data}),//AD conversion results as data input 105 //.a({4'd0,tst_data[11:0]}),//AD Transform results as data input 106 .en(rdy_work),//Coefficient configuration is completed before enabling 107 .coe_data_in16(data_bank),//Initialization Coefficient Data Input 108 .wr_coe_addr(~wr_blk_addr[3:0]),//Address Input of Initialization Coefficient 109 ////!!!Particular attention is paid here to the fact that the multiply-add data enters the multiply-add operation from the large address, so the address requires a complement to flip the coefficients. Amount to: fliplr();!!!!!// 110 .wr_coe_clk(clk),//Initialization Coefficient Writing Clock 111 .wr_coe_en(csh0),//The enabler of coefficient configuration is generated by address decoding of initialization module, which facilitates different coefficients. blk Gating 112 .start(start),//Input Start Convolution Sum fir Control end 113 //.shft_out_dp_data(), 114 .shft_out_dp_data(shft_data1[15:0]), 115 //.s_latch(conv_res) 116 .s_latch(conv_res1[39:0]) 117 ); 118 CONV_SER16 i_conv_ser16_II(//Instantiate the second 16-order convolution/fir Circuit 119 .clk(clk), 120 .a(shft_data1[15:0]),//Data removed from the first section of the cascade 121 .en(rdy_work),//Coefficient configuration is completed before enabling 122 .coe_data_in16(data_bank),//Initialization Coefficient Data Input 123 .wr_coe_addr(~wr_blk_addr[3:0]),//Address Input of Initialization Coefficient 124 ////!!!Particular attention is paid here to the fact that the multiply-add data enters the multiply-add operation from the large address, so the address requires a complement to flip the coefficients. Amount to: fliplr();!!!!!// 125 .wr_coe_clk(clk),//Initialization Coefficient Writing Clock 126 .wr_coe_en(csh1),//The enabler of coefficient configuration is generated by address decoding of initialization module, which facilitates different coefficients. blk Gating 127 .start(start),//Input Start Convolution Sum fir Control end 128 .shft_out_dp_data(shft_data2[15:0]), 129 .s_latch(conv_res2[39:0]) 130 ); 131 CONV_SER16 i_conv_ser16_III(//Instantiate the third 16-order convolution/fir Circuit 132 .clk(clk), 133 .a(shft_data2[15:0]),//Data removed from the first section of the cascade 134 .en(rdy_work),//Coefficient configuration is completed before enabling 135 .coe_data_in16(data_bank),//Initialization Coefficient Data Input 136 .wr_coe_addr(~wr_blk_addr[3:0]),//Address Input of Initialization Coefficient 137 ////!!!Particular attention is paid here to the fact that the multiply-add data enters the multiply-add operation from the large address, so the address requires a complement to flip the coefficients. Amount to: fliplr();!!!!!// 138 .wr_coe_clk(clk),//Initialization Coefficient Writing Clock 139 .wr_coe_en(csh2),//The enabler of coefficient configuration is generated by address decoding of initialization module, which facilitates different coefficients. blk Gating 140 .start(start),//Input Start Convolution Sum fir Control end 141 .shft_out_dp_data(shft_data3[15:0]), 142 .s_latch(conv_res3[39:0]) 143 ); 144 CONV_SER16 i_conv_ser16_IV(//Instantiate the fourth 16-order convolution/fir Circuit 145 .clk(clk), 146 .a(shft_data3[15:0]),//Data removed from the first section of the cascade 147 .en(rdy_work),//Coefficient configuration is completed before enabling 148 .coe_data_in16(data_bank),//Initialization Coefficient Data Input 149 .wr_coe_addr(~wr_blk_addr[3:0]),//Address Input of Initialization Coefficient 150 ////!!!Particular attention is paid here to the fact that the multiply-add data enters the multiply-add operation from the large address, so the address requires a complement to flip the coefficients. Amount to: fliplr();!!!!!// 151 .wr_coe_clk(clk),//Initialization Coefficient Writing Clock 152 .wr_coe_en(csh3),//The enabler of coefficient configuration is generated by address decoding of initialization module, which facilitates different coefficients. blk Gating 153 .start(start),//Input Start Convolution Sum fir Control end 154 .shft_out_dp_data(shft_data4[15:0]), 155 .s_latch(conv_res4[39:0]) 156 ); 157 PADD i_PADD (//For convenience DA Output biases all outputs to positive numbers 158 .clock ( start ), 159 .data0x ( conv_res1[31:0] ), 160 .data1x ( conv_res2[31:0] ), 161 .data2x ( conv_res3[31:0] ), 162 .data3x ( conv_res4[31:0] ), 163 .result ( acc_sum[33:0] ) 164 ); 165 166 MCP4822 i_mcp4822(.clk100m(clk), 167 .rst_n(rdy_work), 168 .start(start), 169 .dac_data_a(data_cha),//passageway a Output data 170 //.dac_data_b(dds_data12),//passageway b Connect DDS content 171 //.dac_data_b(product12),//passageway b High 12-bit join multiplication 172 //.dac_data_b(conv_data12),//passageway b The result of join convolution 173 .dac_data_b(data_chb),//passageway b Output data 174 .cs(cs_da), 175 .mosi(mosi_da), 176 .sck(sck_da), 177 .ld(ld_da) 178 ); 179 MCP3202 i_mcp3202( 180 .clk100m(clk), 181 .rst_n(rdy_work), 182 .start(start), 183 .adc_data_a(ad_data), 184 .cs(cs_ad), 185 .mosi(mosi_ad), 186 .miso(miso_ad), 187 .sck(sck_ad) 188 ); 189 190 sub_offset i_sub_offset (//This subtractor is used from AD The result is a 16-bit complement when the DC bias is removed. 191 .dataa ( {4'd0,acc_sum[26:15]} ),//Convolution results for calculation 192 //.dataa ( {4'd0,ad_data[11:0]} ),//AD It turns out to be a positive integer, with a 16-bit complement to zero. 193 .datab ( 16'h0000 ),//DC bias is considered to be 1/2 full range 16'h0800，No DC bias is 16'h0000 194 .result ( ac_sig[15:0] )//After removing DC bias, the result is 16. bit Complement code 195 ); 196 197 pow_cal i_pow_cal (//Square operation to calculate signal energy 198 .dataa ( ac_sig[15:0] ), 199 .result ( pow_sig[31:0] ) 200 ); 201 202 shft_reg i_shft_reg (//Instantiated shift register 203 .clock ( start ), 204 .shiftin ( pow_sig[31:0] ), 205 .shiftout ( shiftout[31:0] ), 206 .taps ( ) 207 ); 208 sub_add sub_add_inst (//A subtractor that subtracts the number to be taken from the cumulative result by the number fed into the cumulative result. The result may be negative. 209 //After subtraction, it is fed into the accumulator to maintain the contents of the accumulator: the sum of the latest 64 210 .dataa ( pow_sig[31:0] ), 211 .datab ( shiftout[31:0]), 212 .result ( acc_in[31:0] ) 213 ); 214 ////////Calculate the sum of the nearest 64 numbers///////// 215 always @ (posedge start or negedge rst_n) 216 begin 217 if(!rst_n) 218 acc_out[39:0] <= 40'd0; 219 else begin 220 acc_out[39:0] = $signed(acc_out[39:0]) + $signed(acc_in[31:0]); 221 end 222 end 223 ///////Increasing the Resolution of Small Signals by Accumulating and Reciprocating 224 ip_sqrt ip_sqrt_inst ( 225 .radical ( acc_out[39:0] ), 226 .q ( data_out[19:0] ), 227 .remainder ( ) 228 ); 229 endmodule
Most of the above top-level design documents are examples and connection statements of each functional module circuit. Because the code annotations are very detailed, the details will not be repeated here. I mainly introduce the following points:
1. There is only one always procedure assignment statement, which maintains the work of the counter cnt[15:0]. The total synchronous start signal is generated when cnt[15:0] is a specific value, so the period of cnt[15:0] technology also determines the period of start signal, that is, the period of signal.
2. As I prepared for this series“ Control Hardware Interface with Verilog-HDL State Machine ” The advantage of using A/D and D/A to debug the algorithm of FPGA is that the signal of each intermediate node in the algorithm can be presented through D/A converter. The assignment of data_cha[11:0] and data_chb[11:0] in the code has a large number of optional annotations, which are reserved for this reason.
3. In the instantiation code of CONV_SER16 for each convolution section, the interface wr_coe_addr is the initial write address of the coefficient memory (for the content of the initialization part of the coefficient memory, see the description in the second blog article of this series, "Implementing the cross-correlation/convolution/FIR circuit". But when connecting, wr_coe_addr reverses the address wr_blk_addr of the output of the coefficient initializer, because each convolution section multiplies the input first by the content of the coefficient memory with a larger address, so the address should be flipped. Otherwise, the complete sequence of coefficients stored in the coefficient initialization pool will be reversed in each convolution section, which will not produce the correct results.
IV. Test results
The results of FPGA synthesis for Cyclone-I in Quartus-II are shown in the following figure.
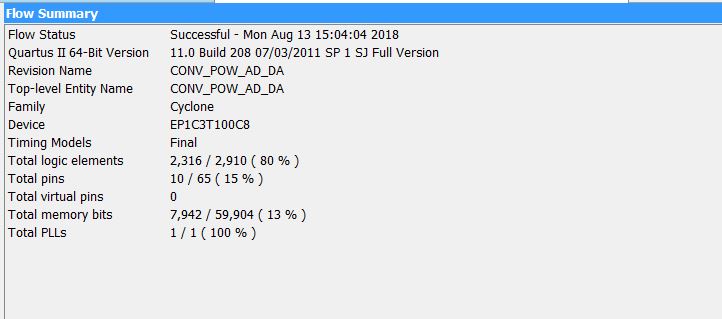
Figure 5 Results of synthesis, layout and wiring
Using matlab to generate 6 sinusoidal cycles of signals with 60 sampling points in length, two zeros are added before and after the signals, thus the sinusoidal signals with 64 sampling points in length are obtained. The reason why 60 sampling points contain 6 sinusoidal cycles is to simulate the sampling rate of 5KHz sinusoidal signal @50KSPS. Finally, the blackman window is added to 64 sampling points to reduce the impact of leakage.
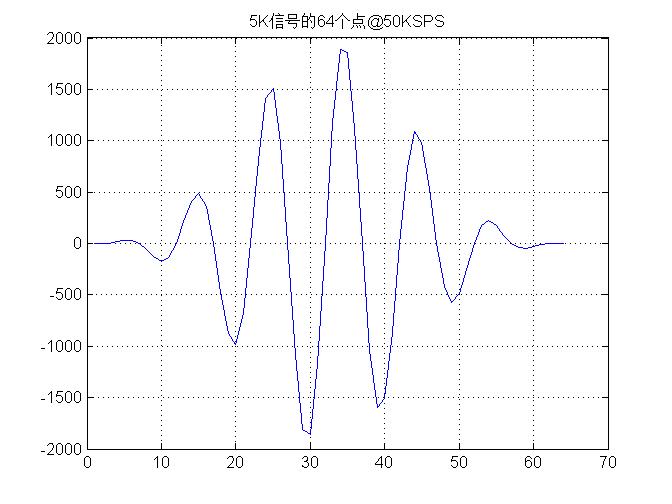
Figure 6 Ideal target reflection echo signal
I downloaded the signal to SideTech arbitrary signal generator 33521 and manually triggered 33521 to generate the waveform shown above to simulate the theoretical echo signal. Connect it to the A/D input of the FPGA platform, and output the processing results from the D/A of the FPGA platform. Observing input and processing results with an oscilloscope is shown in the following figure.
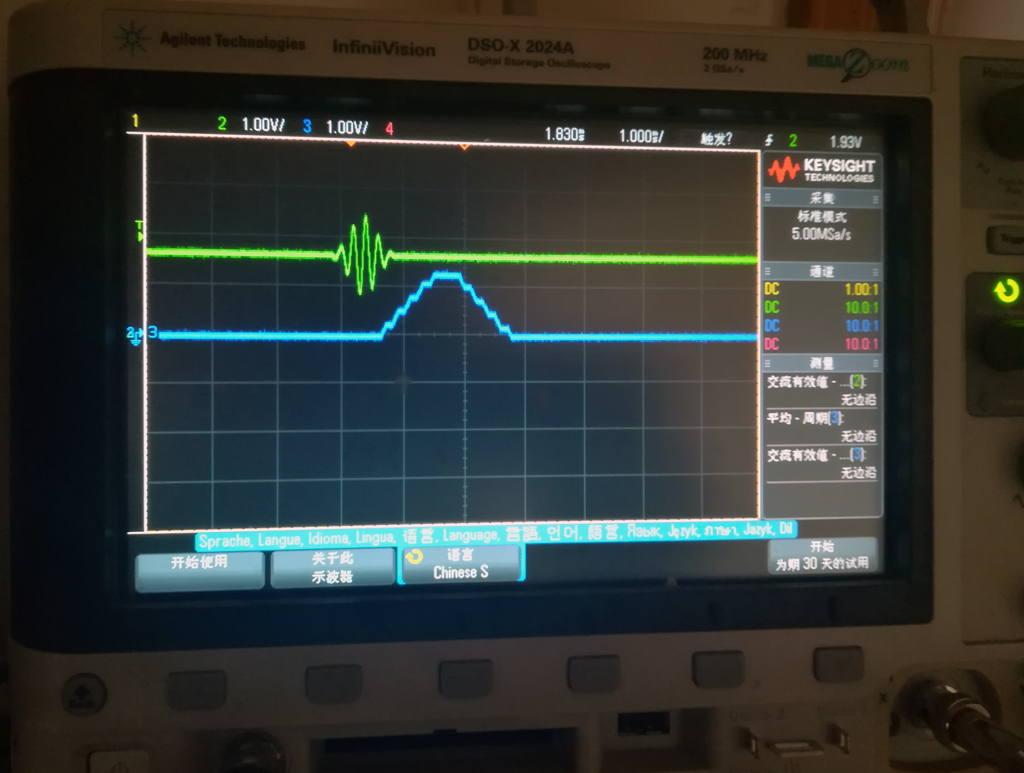
Figure 7 Processing results of field measurements
The above figure shows that the algorithm in the FPGA realizes the output waveform simulated by matlab theory in the first part of this series of blog posts, which can meet the requirements of the target echo detection algorithm. The delay of blue convolution results is due to the latency of the FPGA algorithm, which does not affect the real-time performance of the system.
Of course, what we have accomplished here is only a validation experiment of the algorithm. If we want to really use it, we need to further improve the speed of A/D and D/A conversion.
For the principle and implementation of target echo detection algorithm, please start with the beginning of this series of blog posts.[ Target Reflected Echo Detection Algorithms and Their Implementation on FPGA: An Overview of Algorithms].