preface

We will release Triton 1.0, an open source Python like programming language that enables researchers without CUDA experience to write efficient GPU code - in most cases equivalent to the code generated by experts. Triton makes it possible to reach the peak of hardware performance with relatively little effort; For example, it can be used to write FP16 matrix multiplication kernel, and its performance is equivalent to cuBLAS - which many GPU programmers can't do under 25 lines of code. Our researchers have used it to write a kernel twice as efficient as the equivalent Torch implementation. We are happy to work with the community to make GPU Programming easier for everyone.
New research ideas in the field of deep learning are generally realized by the combination of local framework operators. Although convenient, But this approach often needs to be created (mobile) many temporary tensors, which may reduce the scale performance of neural networks. These problems can be alleviated by writing a special GPU kernel, but this may be surprisingly difficult due to the many complexities of GPU Programming. Moreover, although various systems have emerged recently to simplify this process, we find that they are either too verbose or lack flexibility Either the generated code is significantly slower than our manually adjusted baseline. This prompted us to extend and improve Triton, the latest language and compiler, whose original developers now work in OpenAI.
Triton code
Triton document

Difficulties in GPU Programming

The architecture of modern GPU can be roughly divided into three main parts - DRAM, SRAM and ALU - each part must be considered when optimizing CUDA code.

• Memory transfers from DRAM must be condensed into large transactions to take advantage of the large bus width of modern memory interfaces.
• Before reuse, the data must be manually stored in SRAM and managed to minimize the conflict of shared memory library during retrieval.
• Computing must be carefully divided and arranged between and within streaming multiprocessors (SM) to promote instruction / thread level parallelism and take advantage of special-purpose ALU s (such as tensor cores)

The basic architecture of GPU is as follows:

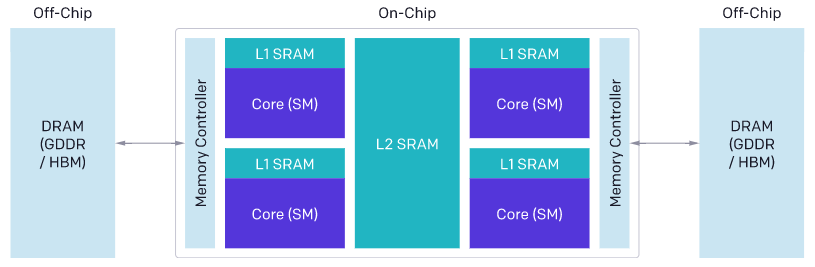
Reasoning about all these factors is challenging, even for experienced CUDA programmers with many years of experience. Triton's goal is to fully automate these optimizations so that developers can better focus on the high-level logic of their parallel code. Triton's goal is to be widely applicable, so it will not automatically arrange cross SM work - leaving some important algorithm considerations (such as tiling, synchronization between SM) to the developer's decision.
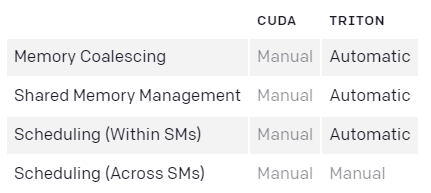
The comparison of compiler optimizations in CUDA and Triton is as follows:

Programming model

Of all the domain specific languages and JIT compilers available, Triton is perhaps the most similar to Numba: the kernel is defined as decorated Python functions with different programs on the grid of so-called instances_ ID concurrent startup. However, as the following code snippet shows, that's all the similarity. By operating on the block, Triton exposes the parallelism within the instance, rather than the execution model of single instruction multithreading (SIMT) 7, and the block size is a power of 2. In this way, Triton effectively abstracts all problems related to concurrency within CUDA thread blocks (e.g., memory aggregation, shared memory synchronization / collision, tensor core scheduling).

The following is vector addition in Numba:

BLOCK = 512

# This is a GPU kernel in Numba.
# Different instances of this
# function may run in parallel.
@jit
def add(X, Y, Z, N):
   # In Numba/CUDA, each kernel 
   # instance itself uses an SIMT execution
   # model, where instructions are executed in
   # parallel for different values of threadIdx
   tid = threadIdx.x
   bid = blockIdx.x
   # scalar index
   idx = bid * BLOCK + tid
  if id < N:
     # There is no pointer in Numba.
     # Z,X,Y are dense tensors
     Z[idx] = X[idx] + Y[idx]


...
grid = (ceil_div(N, BLOCK),)
block = (BLOCK,)
add[grid, block](x, y, z, x.shape[0])

The following is vector addition in Triton:

BLOCK = 512

# This is a GPU kernel in Triton.
# Different instances of this
# function may run in parallel.
@jit
def add(X, Y, Z, N):
   # In Triton, each kernel instance
   # executes block operations on a
   # single thread: there is no construct
   # analogous to threadIdx
   pid = program_id(0)
   # block of indices
   idx = pid * BLOCK + arange(BLOCK)
   mask = idx < N
   # Triton uses pointer arithmetics  
   # rather than indexing operators
   x = load(X + idx, mask=mask)
   y = load(Y + idx, mask=mask)
   store(Z + idx, x + y, mask=mask)


...
grid = (ceil_div(N, BLOCK),)
# no thread-block
add[grid](x, y, z, x.shape[0])

Although this may not be particularly helpful for embarrassing parallel (i.e. element by element) computing, it can greatly simplify the development of more complex GPU programs.
For example, consider the case of fusing the softmax kernel, where each instance normalizes different rows of a given input tensor X X ∈ R M × N X \in \mathbb{R}^{M\times N} X∈RM × N. The standard CUDA implementation of this parallelization strategy can be challenging to write, requiring explicit synchronization between threads because they reduce the same line of X at the same time. Most of this complexity disappears in Triton. Each kernel instance loads the rows of interest and standardizes them sequentially using primitives similar to NumPy.
Write the fused softmax code in triton as follows:

import triton
import triton.language as tl

@triton.jit
def softmax(Y, stride_ym, stride_yn, X, stride_xm, stride_xn, M, N):
    # row index
    m = tl.program_id(0)
    # col indices
    # this specific kernel only works for matrices that 
    # have less than BLOCK_SIZE columns
    BLOCK_SIZE = 1024
    n = tl.arange(0, BLOCK_SIZE)
    # the memory address of all the elements
    # that we want to load can be computed as follows
    X = X + m * stride_xm + n * stride_xn
    # load input data; pad out-of-bounds elements with 0 
    x = tl.load(X, mask=n < N, other=-float('inf'))
    # compute numerically-stable softmax
    z = x - tl.max(x, axis=0)
    num = tl.exp(z)
    denom = tl.sum(num, axis=0)
    y = num / denom
    # write back to Y
    Y = Y + m * stride_ym + n * stride_yn
    tl.store(Y, y, mask=n < N)

import torch
# Allocate input/output tensors
X = torch.normal(0, 1, size=(583, 931), device='cuda')
Y = torch.empty_like(X)
# SPMD launch grid
grid = (X.shape[0], )
# enqueue GPU kernel
softmax[grid](Y, Y.stride(0), Y.stride(1), 
              X, X.stride(0), X.stride(1),
              X.shape[0]    , X.shape[1])

Note that the Triton JIT treats X and Y as pointers, not tensors; We believe that preserving low-level control over memory access is important for solving more complex data structures (e.g., block sparse tensors).

Importantly, this particular implementation of softmax keeps the rows of X in SRAM throughout the normalization process, This maximizes the reuse of data when applicable (~ < 32K columns). This is different from the internal CUDA code of PyTorch, which uses temporary memory to make it more general, but the speed is significantly slower (as follows). The bottom line here is not that Triton is inherently better, but that it simplifies the development of special kernels and can be much faster than the kernels in the general library.
When M=4096, the performance of A100 processing fused Softmax is as follows:

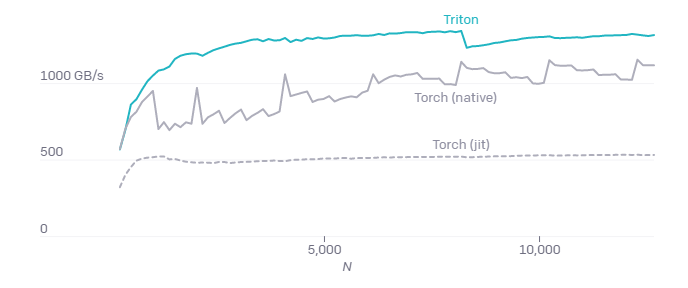
The low performance of Torch (v1.9) JIT highlights the difficulty of automatically generating CUDA code from high-level tensor operation sequences.

@torch.jit.script
def softmax(x):
    x_max = x.max(dim=1)[0]
    z = x - x_max[:, None]
    numerator = torch.exp(x)
    denominator = numerator.sum(dim=1)
    return numerator / denominator[:, None]

Matrix multiplication

It is very important to write a fusion kernel for element operation and reduction, but considering the prominence of matrix multiplication task in neural network, this is far from enough. Triton has also proved very effective for these tasks, reaching peak performance in only about 25 lines of Python code. On the other hand, implementing something similar in CUDA will take more effort and may even achieve lower performance. The following is the matrix multiplication code in Triton:

@triton.jit
def matmul(A, B, C, M, N, K, stride_am, stride_ak, 
            stride_bk, stride_bn, stride_cm, stride_cn,
            **META):
    # extract metaparameters
    BLOCK_M, GROUP_M = META['BLOCK_M'], META['GROUP_M']
    BLOCK_N = META['BLOCK_N']
    BLOCK_K = META['BLOCK_K']
    # programs are grouped together to improve L2 hit rate
    _pid_m = tl.program_id(0)
    _pid_n = tl.program_id(1)
    pid_m = _pid_m // GROUP_M
    pid_n = (_pid_n * GROUP_M) + (_pid_m % GROUP_M)
    # rm (resp. rn) denotes a range of indices
    # for rows (resp. col) of C
    rm = pid_m * BLOCK_M + tl.arange(0, BLOCK_M)
    rn = pid_n * BLOCK_N + tl.arange(0, BLOCK_N)
    # rk denotes a range of indices for columns 
    # (resp. rows) of A (resp. B)
    rk = tl.arange(0, BLOCK_K)
    # the memory addresses of elements in the first block of
    # A and B can be computed using numpy-style broadcasting
    A = A + (rm[:, None] * stride_am + rk[None, :] * stride_ak)
    B = B + (rk [:, None] * stride_bk  + rn[None, :] * stride_bn)
    # initialize and iteratively update accumulator
    acc = tl.zeros((BLOCK_M, BLOCK_N), dtype=tl.float32)
    for k in range(K, 0, -BLOCK_K):
        a = tl.load(A)
        b = tl.load(B)
        # block level matrix multiplication
        acc += tl.dot(a, b)
        # increment pointers so that the next blocks of A and B
        # are loaded during the next iteration
        A += BLOCK_K * stride_ak
        B += BLOCK_K * stride_bk
    # fuse leaky ReLU if desired
    # acc = tl.where(acc >= 0, acc, alpha * acc)
    # write back result
    C = C + (rm[:, None] * stride_cm + rn[None, :] * stride_cn)
    mask = (rm[:, None] < M) & (rn[None, :] < N)
    tl.store(C, acc, mask=mask)

An important advantage of the handwritten matrix multiplication kernel is that they can be customized as needed to adapt to the fusion transformation of its input (such as slice) and output (such as Leaky ReLU). Without a system like Triton, the non substantive modification of the matrix multiplication kernel is out of reach for developers without special GPU programming expertise.

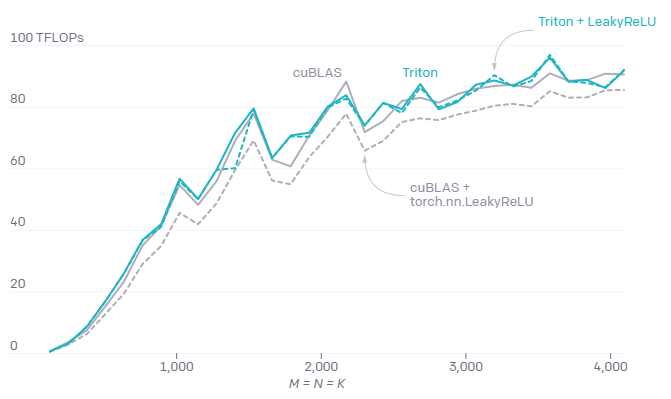
Advanced system architecture

Triton's good performance comes from the modular system architecture centered on Triton IR. Triton IR is an intermediate representation based on LLVM, in which multi-dimensional value blocks are more important.

@triton. The JIT decorator works by traversing the abstract syntax tree of the provided Python functions (AST) to quickly generate Triton IR using common SSA construction algorithms. Then, the generated IR code is simplified, optimized and automatically parallelized by our compiler backend, and then converted to high-quality LLVM-IR, and finally PTX, for execution on the recent NVIDIA GPU. At present, CPU and AMD GPU are not supported, but we welcome the community's contribution to solve this problem Offer.

Compiler backend

We found that our compiler can automatically perform various important program optimizations by using block program representation through Triton IR. For example, by viewing the operands of compute intensive block level operations (such as tl.dot), data can be automatically stored in shared memory and allocated / synchronized using standard validity analysis techniques.

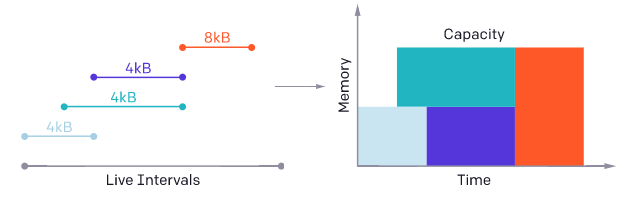
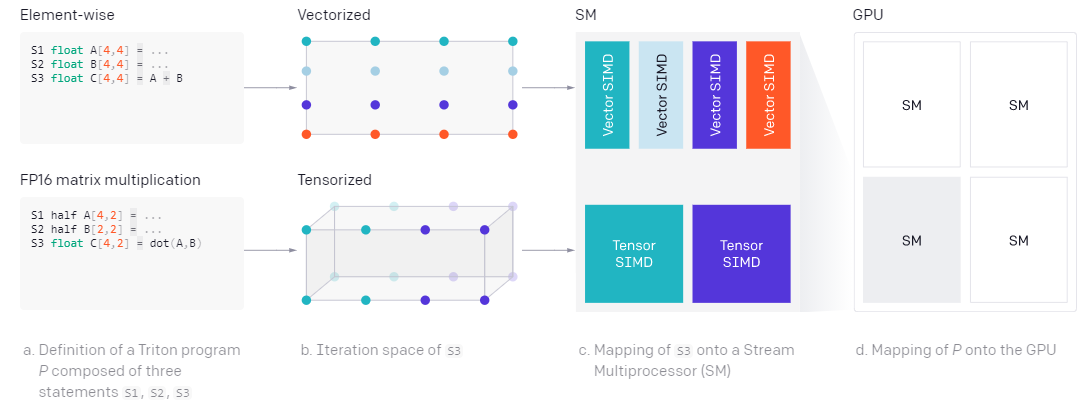
On the other hand, Triton program can effectively and automatically parallelize: (1) parallelize SM by executing different kernel instances concurrently; (2) Within SM, the iteration space of each block level operation is analyzed and fully divided among different SIMD units, as shown below.

Reference link: https://openai.com/blog/triton/.